Задачи к контрольной работе
Выполнение письменной контрольной работы имеет большое значение в учебном процессе, так как способствует закреплению и проверке знаний, полученных на лекциях и практических занятиях, а также в процессе самостоятельного изучения учебного материала. Цель контрольной работы – приобрести практические навыки при построении экономической модели и ее решении. Номер задач контрольной работы определяется по таблице. Замена варианта работы самим студентом запрещается.
При выполнении контрольной работы необходимо руководствоваться соблюдением следующих требований:
1. На титульном листе должны быть указаны: фамилия, имя и номер варианта задания.
2. Решения задач должны быть расположены в порядке номеров.
3. Перед решением задачи следует письменно воспроизвести ее условие.
4. Решение задачи излагается подробно с приведением формул, развернутых расчетов и пояснением всех действий. Задачи, в которых даны только ответы без промежуточных вычислений, считаются нерешенными.
5. Вычисления производятся с точностью до 0,001. Единицы измерения и их обозначения должны соответствовать общепринятым.
6. Контрольная работа должна быть аккуратно оформлена, написана разборчиво, без помарок и зачеркиваний, без сокращения слов (кроме общепринятых сокращений).
7. Страницы работы необходимо пронумеровать и иметь поля (3 см.) для замечаний рецензента.
8. После получения прорецензированной работы студент должен исправить все отмеченные ошибки и недочеты, внести необходимые дополнения. Без выполнения этих требований студент не допускается к защите. В случае незачета контрольной работы все задания выполняются заново.
Номера задач согласно шифра
Задача 1.
Решить задачу коммивояжера для 5 пунктов. Матрицы по парных расстояний между пунктами по вариантам представлены в приложении № 1. Расстояние, равное ∞, соответствует тому, что данный маршрут не существует.
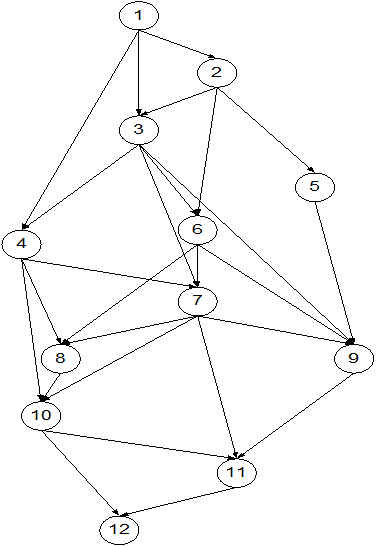 рисунок 1 рисунок 1
|
Задача 2.
На основе сетевого графика (рисунок 1) определить: критический путь, резервы событий, а также полные и свободные резервы операций по заданным условиям приложения № 2, где в скобках указаны направленные дуги сетевого графика: первая цифра — номер вершины, из которой дуга исходит, вторая — вершина, куда входит. В соседнем столбце указаны продолжительности выполнения работ, соответствующих дугам.
Задача 3.
Упростить игру «n x m» (приложение № 3) до игры «2 х 2» и решите ее графическим методом и методом опций.
Задача 4.
Найти решение игр «2 х n» и «m х 2» (приложение № 4).
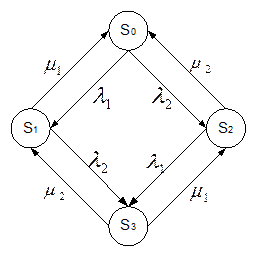 рисунок 2
рисунок 2
|
Задача 5.
Рассмотрим процесс с дискретным состоянием и непрерывным временем: техническое устройство S состоит из двух узлов, каждый из которых в случайный момент времени может выйти из строя (отказать), после чего мгновенно начинается ремонт узла, тоже продолжающееся заранее неизвестное, случайное время. Возможные состояния системы можно перечислить: S0 - оба узла исправны; S1 - первый узел ремонтируется, второй работает; S2 - второй узел ремонтируется, первый работает и S3 - оба узла ремонтируются.
Рассчитать финальные вероятности (р0, р1, р2, р3) состояния системы по схеме, представленной на рисунке 2, если: λ1, λ2, μ1, μ2 – даны в приложении №5.
Задача 6.
В справочном бюро работает 5 телефонисток, найдите финальные вероятности и характеристики эффективности по данным приложения № 6, если интенсивность потока заявок λ телефонных звонков в минуту, а среднее время обслуживания одной заявки  минут (все потоки событий простейшие):
минут (все потоки событий простейшие):
1. для СМО с отказом
2. для СМО с неограниченной очередью (рассчитав финальные вероятности с точностью до 5 звонков в очереди).
Задача 7.
Ориентируясь на матрицу прямых затрат А (приложение № 7) определить:
1. Валовую продукцию каждой отрасли х1, х2, х3, х4 при условии, что каждый платежеспособный спрос на продукцию отраслей в прогнозном периоде в сопоставимых ценах составит соответственно (смотри приложение № 7) ỹ1, ỹ2, ỹ3, ỹ4.
2. Конечное использование продукцию каждой из отраслей у1, у2, у3, у4 при условии, что валовой выпуск отраслей в прогнозном периоде в сопоставимых ценах составит соответственно х1, х2, х3, х4 (смотри приложение № 7).