Отчет о выполнении работы 1.1
Министерство образования Республики Беларусь
Учреждение образования «Международный государственный экологический университет им. А.Д. Сахарова»
Отчет о выполнении лабораторной работы №1
Изучение статистических ошибок, возникающих при измерении фонового излучения в лаборатории. Определение размеров и объемов твердых тел правильной формы.
Выполнила :
студентка 1 курса
Факультета экологической
медицины
Группы 12062/2
Шатуха Дарья
Минск 2012
Теоретическая часть
Для оценки точности измерений обычно применяют величину, называемую дисперсией. Дисперсией  случайной величины называется среднее значение квадрата отклонения этой величины от ее среднего значения:
случайной величины называется среднее значение квадрата отклонения этой величины от ее среднего значения:
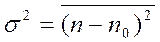
Сама величина  (корень квадратный из дисперсии) называется среднеквадратичной ошибкой или стандартным отклонением.
(корень квадратный из дисперсии) называется среднеквадратичной ошибкой или стандартным отклонением.
Обратимся теперь к следующему важному вопросу. Пусть мы провели серию из N измерений, в результате которой получены значения мощности n1, n2,..., nN . Эти результаты мы до сих пор использовали для того, чтобы определить, как отличаются друг от друга значения, полученные в разных измерениях. Как уже отмечалось, этот вопрос важен главным образом для выяснения того, насколько достоверен результат, полученный в одном измерении. Но если было проведено несколько измерений, их результаты могут быть использованы и с другой целью: они позволяют определить среднее значение измеряемой величины точнее, чем это можно сделать, если произведено всего одно измерение. При N измерениях среднее значение мощности экспозиционной дозы излучения равно, очевидно,
 , (1)
, (1)
а стандартная ошибка отдельного измерения, по определению, равна
 , (2)
, (2)
Величина  из формулы (1), полученная путем усреднения результатов по серии из N опытов, конечно, тоже не вполне точно совпадает с истинным средним значением
из формулы (1), полученная путем усреднения результатов по серии из N опытов, конечно, тоже не вполне точно совпадает с истинным средним значением  , и сама является случайной величиной, но отклонение величины
, и сама является случайной величиной, но отклонение величины  от
от  ,вообще говоря, существенно меньше, чем
,вообще говоря, существенно меньше, чем  .
.
Теория вероятностей показывает, что стандартная ошибка отклонения  от
от  может быть определена по формуле:
может быть определена по формуле:
 , (3)
, (3)
Обычно наибольший интерес представляет не абсолютная, а относительная точность измерений. Для рассмотренной серии из N измерений относительная ошибка отдельного измерения (т.е. ожидаемое отличие любого из  от
от  ) равна
) равна
 .
.
Аналогичным образом относительная ошибка в определении среднего по всем измерениям значения  равна
равна
 . (4)
. (4)
Таким образом, относительная точность измерения  определяется полным числом значений
определяется полным числом значений  . Этого, конечно, и следовало ожидать, так как все измерения вместе составляют одно более продолжительное измерение. Как мы видим, относительная точность измерения постепенно улучшается с увеличением числа экспериментов.
. Этого, конечно, и следовало ожидать, так как все измерения вместе составляют одно более продолжительное измерение. Как мы видим, относительная точность измерения постепенно улучшается с увеличением числа экспериментов.
Вычисление объема тела относится к косвенным измерениям, т.к. искомая величина задается как некоторая функция других величин, определяемых путем прямых измерений, в нашем случае параметров (длины, высоты и ширины).
Если исследуемая величина А равна сумме или разности двух измеренных величин
 , (6)
, (6)
то наилучшее значение величины (среднее арифметическое) А равно сумме (или разности) наилучших значений слагаемых:
 . (7)
. (7)
Среднеквадратичная погрешность sА , если величины В и С независимы находится по формуле:
 (8)
(8)
В случае, когда искомая величина равна произведению или частному двух других,
 (9)
(9)
то искомая величина равна произведению или частному средних значений, измеренных величин.
Среднеквадратичная погрешность произведения и частного независимых величин находится по формуле:

 (10)
(10)
Т.к. в реальных условиях опыта присутствуют как систематические, так и случайные ошибки, суммарная погрешность находится по формуле:
 (11)
(11)
Отчет о выполнении работы 1.1
Принадлежности: Дозиметр ДБГ-06Т.
Проверим правильность работы ДБГ-06Т.
Данные измерений мощности экспозиционной дозы излучения, ni мкР/ч:
Таблица 1.
| № опыта | ||||||||||
3. Представим результаты опыта в виде, удобном для построения гистограммы
(таблица 2). Построим гистограмму Wn=f(n) :
Таблица 2
| Значение мощности (ni ) экспозиционной дозы (мкР/ч) | |||||||||||||
| Число случаев наблюдений | |||||||||||||
| Доля случаев Wn | 0.01 | 0.03 | 0.03 | 0.07 | 0.08 | 0.14 | 0.24 | 0.1 | 0.11 | 0.08 | 0.08 | 0.02 | 0.01 |

4. Представим результаты опыта в таблице в удобном для промежуточных расчетов виде (таблица 3) и используя формулу (1), определим среднее значение мощности экспозиционной дозы излучения:
Таблица 3
| Значение мощности (ni ) экспозиционной дозы (мкР/ч) | Число случаев наблюдений | Доля случаев наблюдений | åni |
Dni = ni -  (мкР/ч)
(мкР/ч)
|
( Dni )2=
( ni -  )2 )2
|
å
( ni -  )2 )2
| ||
| 0,01 | -6,2 | 38,44 | 38,44 | |||||
| 0,03 | -5,2 | 27,04 | 81,12 | |||||
| 0,03 | -4,2 | 17,64 | 52,92 | |||||
| 0,07 | -3,2 | 10,24 | 71,68 | |||||
| 0,08 | -2,2 | 4,84 | 38,72 | |||||
| 0,14 | -1,2 | 1,44 | 20,16 | |||||
| 0,24 | -0,2 | 0,04 | 0,96 | |||||
| 0,1 | 0,8 | 0,64 | 6,4 | |||||
| 0,11 | 1,8 | 3,24 | 35,64 | |||||
| 0,08 | 2,8 | 7,84 | 62,72 | |||||
| 0,08 | 3,8 | 14,44 | 115,52 | |||||
| 0,02 |
| 4,8 | 23,04 | 46,8 | ||||
| 0,01 | 5,8 | 33,64 | 33,64 | |||||
| å1320 | å604,72 |
 мкР/ч
мкР/ч
5. Найдем стандартную ( среднеквадратичную) ошибку отдельного измерения используя таблицу 3 и формулу (2),:
 »2,5 мкР/ч
»2,5 мкР/ч
Округлим результат расчета, т.к. первая значащая цифра 6, то округлим до одной значащей цифры.
6. Отметим на гистограмме среднее значение мощности экспозиционной дозы  , округленное с учетом среднеквадратичной ошибки, а также значения
, округленное с учетом среднеквадратичной ошибки, а также значения  :
:
 мкР/ч
мкР/ч
7.Измерим на гистограмме полуширину распределения, т.е. половину ширины гистограммы на уровне половины высоты. Сравним полученное значение с величиной  .
.
Половина высоты: 
Полуширина распределения (19-13)/6 = 6/2 = 1 мкР/ч
 = 6 мкР/ч
= 6 мкР/ч
Сравним эти величины в процентном соотношении  .
.
Вывод: величины различаются на 42%. Поскольку точность используемой методики оценки погрешностей составляет 40-50%, то эти величины можно считать равными, и вместо громоздких вычислений  можно просто измерять полуширину гистограммы.
можно просто измерять полуширину гистограммы.
8. Определим долю случаев, когда отклонения от среднего значения  превышают
превышают  , 2
, 2  и сравним с теоретическими оценками:
и сравним с теоретическими оценками:
| Ошибка | Число случаев | Доля случаев | Теоретическая оценка |
±  = ± 2,5 = ± 2,5
| 14+19=33 | 1-0,68=0,32 | |
± 2  = ±3,5 = ±3,5
| 4+3=7 | 0,01 | 1-0,95=0,05 |
9. Определим стандартное отклонение величины  , используя всю совокупность измерений по формуле (3):
, используя всю совокупность измерений по формуле (3):  мкР/ч
мкР/ч
10. Найдем относительную ошибку этого результата по первому равенству (4):

11. Окончательный результат, с учетом округления среднего значения в соответствии со стандартной ошибкой серии измерений:
n = (13,2 ± 0,25) мкР/ч .
Вывод: истинный результат измерения мощности экспозиционной дозы излучения с вероятностью 68 % находится с диапазоне 12,95¸15,7 мкР/ч.