Определение площадей земельных участков по измерениям на местности (аналитический способ)
Когда имеются небольшие участки на местности и координаты поворотных точек границы неизвестны или нецелесообразно прокладывать теодолитный ход, то участок можно разделить на простейшие геометрические фигуры (чаще треугольники, реже прямоугольники), площади которых можно определить аналитически по формулам геометрии, тригонометрии или аналитической геометрии. При этом могут возникнуть следующие случаи:

Рис. 7.1. Схема треугольника.
1)Треугольник(рис.7.1). При этом площадь определяется по известным формулам:
2Р=аh (7.1)
или
2P=aвsinβ. (7.2)
Когда участок треугольной формы, то целесообразнее применить формулу (7.2), для чего на местности измеряют две стороны и угол между ними.
2)Четырехугольник (рис.7.2). Для четырехугольника у которого известны три стороны a, в, c и углы β1 и β2, заключенные между ними, можно вывести формулу для определения площади.
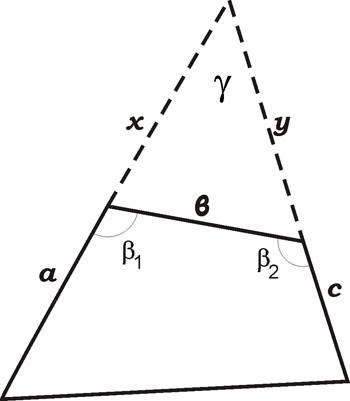
Рис. 7.2. Схема четырехугольника
Из чертежа (рис. 7.2) видно, что площадь Р четырехугольника может быть представлена, как разность площадей большого треугольника со сторонами (а+х) и (с+у) и углом между ними γ и малого со сторонами х, у и углом между ними γ, т.е.
2Р=(а+х)(с+у)sinγ-хуsinγ=(ас+хс+ау+ху))sinγ-хуsin γ = ас sin γ +хс sin γ+ау sin γ + х у sin γ - х уsin γ. (7.3)
Но из чертежа видно, что угол γ в малом треугольнике можно выразить через известные (измеренные) углы β1 и β2, т.е.
γ = 180º - (180º- β1) -(180º - β2)= β1 + β2-180º. (а)
В малом треугольнике известны три угла и одна сторона в, тогда по теореме синусов можно определить остальные стороны, т.е.
х/sin(180º- β2) = в/ sin γ,
откуда
х= в sin β2/ sin γ. (б)
Аналогично,
у/sin(180º-β1)=в/sin γ,
у= в sin β1/ sin γ. (г)
Подставив значения (а), (б), (г) в выражение (7.3), получим:
2Р= авsinβ1 +вc sinβ2 + ac sin (β1 + β2 - 180º). (7.4)
3) Трапеция (рис.7.3). Площадь трапеции можно вычислить по двум измеренным основанияма, в и углам β1, β2 при основании.
Известно, что
2Р=(а + в ) h. (7.5)

Рис.7.3. Схема трапеции.
Из чертежа (рис.7.3.) видно, что х+y = а - в,
где х = h ctg β1, у= h ctg β2,
поэтому
х+у = h(ctg β1 + ctg β2) = а -в.
Откуда
h=( а - в )/ (ctg β1 + ctg β2).
Подставим это выражение в формулу (7.5) и получим:
2Р =( а2 - в2)/ (ctg β1 + ctg β2). (7.6)
4) Пятиугольник (рис.7.4).

Рис.7.4 Схема определения площади пятиугольника.
Площадь пятиугольника можно представить как площадь треугольника 1-2-3 ( у которого измерены две стороны и угол между ними) и площадь четырехугольника 1-3-4-5 (у которого измерены три стороны и два угла между ними).
Тогда площадь вычисляют по формуле
2Р= s1s2sinβ +s3s4 sinβ4 + s4s5 sinβ5 + s3s5 sin (β4 + β5 - 180º).
5) Для шестиугольника, когда измерены все стороны и четыре угла между ними используют формулу (7.4) два раза.
Если участок имеет больше шести поворотных точек, то его площадь определяют по координатам или по приращениям координат.
Для вывода формулы определения площади замкнутого полигона по координатам его вершин рассмотрим пятиугольник (рис. 7.5), из вершин которого опущены перпендикуляры на ось ординат. Площадь полигона 1-2-3-4-5 можно выразить через площади трапеций, у которых основаниями являются абсциссы х, а высотами - разности ординат у2 - у1 , у3 - у2 и т. д., поэтому
Р = РА - 1 - 2 - 3 - 4 - В - РА - 1 - 5 - 4 - В = ½ (х1 + х2)(у2 - у1) +½ (х2 + х3)(у3 - у2) +½ (х3 + х4)(у4 - у3) - ½ (х4 + х5)(у4 - у5) - ½ (х5 + х1)(у5 - у1) .

Рис. 7.5. Схема определения площади полигона по координатам его вершин.
Изменив знаки в этом выражении, после сокращений и группировки по х и по у получим
2Р = ∑ (Хк +Хк+1)(Ук+1 -Ук). (7.7)
Раскрыв скобки и произведя замену, получим
2Р = ∑ Ук(Хк-1-Хк+1), (7.8)
2Р = ∑ Хк(Ук+1-Ук-1). (7.9)
т. е. удвоенная площадь полигона равна сумме произведений каждой ординаты на разность абсцисс предыдущей и последующей точек или каждой абсциссы на разность ординат последующей и предыдущей точек. В формулах (7.8-7.9) сумма разностей должна равняться нулю, что является контролем вычисления разностей.
Для определения площади полигона по приращениям координат и координатам вершин полигона из формул (7.8 и 7.9) и можно получить
2Р = ∑ (Хк + Хк+1)Δук (7.10)
или
2Р = ∑ ХкΔук + ∑ Хк+1Δук. (7.11)
При площади полигона до 200 га рекомендуется перед вычислениями округлять координаты до 0,1 м, а при большей - до 1м.
Для вычисления площадей можно использовать формулы, которые получаются из (7.8 и 7.9) после раскрытия скобок.
2Р = ∑ Хк Ук+1 - ∑ Хк Ук -1
или
2Р = ∑ Ук Хк+1 - ∑ Ук Хк -1.
Вычисленная площадь землевладения сравнивается с данными по учёту земель. Расхождения допускаются не более 1/2000.
На ЭВМ вычисление площадей выполняется по специально разработанным программам в соответствии с формулами (7.8, 7.9 и 7.10) независимо от числа точек полигона.
Пример 1. На местности у треугольника измерены основание а = 40,0 м и высота h = 100,0 м.
Площадь вычислим по формуле (7.1), т.е.
Р= 0,5аh = 40,0м х 100,0 м = 2000 м2.
Пример 2. На местности у треугольника измерены стороны а = 40,0 м, b = 100,0м и угол между ними β=40º.
Площадь треугольника вычисляется по формуле
2Р=аbsinβ =40,0 м х 100,0м sin 40º = 1286м2.
Способы определения площадей графическим и механическим способами были подробно рассмотрены в п.п. 4.11 - 4.17.
Вопросы и задачи для самопроверки
1. Какие существуют методы определения площадей? Сопоставьте эти методы по точности.
2. В чем сущность аналитического метода определения площади? Напишите применяемые формулы.
3. В каких случаях применяют графический и в каких механический методы определения площади?
4. Как определяют общую площадь землевладения?
5. Назовите методы определения площадей контуров угодий.
6. Каковы причины возникновения деформации планов и как она учитывается при определении расстояний и площадей по плану?
| к предыдущему разделу | к следующему разделу |