Vzpomeň si na větu o ekvivalentních úpravách skupiny generátorů!!
Matice řádu n
- s n řádky a n sloupci
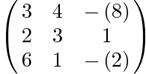
A =
Hlavní a vedlejší diagonála matice
 |
| a11 | a12 | a13 | a14 |
| a21 | a22 | a23 | a24 |
| a31 | a32 | a33 | a34 |
vedlejšíhlavní
diagonála diagonála
Nulová matice typu (m,n)

A =
Jednotková matice řádu n
 |
En =
Kdy se dvě matice A a B rovnají?
A = B , jestliže jsou obě matice stejného typu (m, n)
a navíc
aij = bij pro i = 1, 2, . . . , m
j = 1, 2, . . . , n
Maticové operace
Sčítání maticA, B matice typu (m, n)

A + B =
Násobení matice reálným číslem
 r ∈ R, matice A typu (m,n)
r ∈ R, matice A typu (m,n)
r . A =
věta (o vlastnostech maticových operací):
Nechť A, B a Cjsou matice typu (m, n), r, s ∈ R.
Pak platí
1) A+ B = B+ A, komutativní z.
2) A+ (B + C) = (A + B) + C, asociativní z.
3) r(A + B) = rA + rB, distributivní z.
4) (r + s)A = rA + sA, distributivní z.
5) r(sA) = (rs)A.
věta:
Množina Rmxn všech matic typu (m, n) spolu s operacemi sčítání matic a násobení matice reálným číslem tvoří vektorový prostor dimenze mn.
Hodnost matice
definice:
Hodnostímatice A typu (m, n) rozumíme dimenzi podprostoru Rngenerovaného řádkovými vektory matice A. Hodnost matice A označíme h(A).
Poznámka.Hodnost matice je rovna nejvyššímu počtu lineárně nezávislých řádku matice. Hodnost nulové matice h(O) = 0.
definice:
Řekneme, že matice T typu (m, n) je trojúhelníková matice, jestliže m≤n a pro prvky matice Tplatí
tij = 0 pro j < i a tii ≠ 0 pro i = 1,…, m.
věta:
Je-li matice T typu (m,n) trojúhelníková matice, pak
h(T)=m
Vzpomeň si na větu o ekvivalentních úpravách skupiny generátorů!!
Postup při hledání hodnosti matice A:
1) ekvivalentní úpravy
A ------------------------------> T
2) spočítej počet řádků matice T
definice:
Nechť Aje matice typu (m, n). Transponovanoumaticí k matici Anazveme matici ATtypu (n, m) pro kterou platí, že i-tý řádek matice Aje i-tým sloupcem matice AT.
věta:
Nechť AT je transponovaná matice k matici A, pak platí
h(A) = h(AT).
Poznámka.Označme r1, r2, . . . , rm řádkové vektory, resp. s1, s2, . . . , sn sloupcové vektory matice A. Označme R(A) podprostor Rn generovaný řádkovými vektory matice A a analogicky označme S(A) podprostor Rm generovaný sloupcovými vektory matice A.
Právě uvedená věta tvrdí, že
dim R(A) = dim S(A) .
Prostor R(A) nazýváme řádkovým modulem a prostor S(A) sloupcovým modulemmatice A.
Metoduurčení hodnostimatice lze velmi dobře použítke zjišťování lineární závislosti, resp. nezávislosti skupiny vektorů.