
Категории:
АстрономияБиология
География
Другие языки
Интернет
Информатика
История
Культура
Литература
Логика
Математика
Медицина
Механика
Охрана труда
Педагогика
Политика
Право
Психология
Религия
Риторика
Социология
Спорт
Строительство
Технология
Транспорт
Физика
Философия
Финансы
Химия
Экология
Экономика
Электроника
Переход от описательных параметров к количественным показателям
Формулирование задачи
На начальной стадии стратегического планирования деятельности организации используется SWOT-анализа [29]. При использовании этого метода строится таблица с четырьмя графами:
- сильные стороны (strengths),
- недостатки (weaknesses),
- возможности (oportunities),
- угрозы (threats).
Аббревиатура этих английских слов образует название метода - SWOT-анализ. Две первые графы описывают внутреннюю среду организации. На эти параметры организация может непосредственно влиять. Две последних графы представляют внешнюю среду. На нее организация влиять не может, но события из этих граф определяют деятельность самой организации. Таблица SWOT-анализа показана на рис. 1.
| Внутренняя среда | Сильные стороны | Слабые стороны | Внутренняя среда |
| Организационные факторы | Организационные факторы | ||
| Факторы управления | Факторы управления | ||
| Рыночные факторы | Рыночные факторы | ||
| Технические факторы | Технические факторы | ||
| Финансовые аспекты | Финансовые аспекты | ||
| Внешняя среда | Возможности | Угрозы | Внешняя среда |
| Политическая ситуация | Политическая ситуация | ||
| Экономическая ситуация | Экономическая ситуация | ||
| Социально-культурная ситуация | Социально-культурная ситуация | ||
| Технологическая ситуация | Технологическая ситуация | ||
| Демографическая | Демографическая | ||
Рис. 1.
Этот метод дает возможность менеджерам формализовать и наглядно представить текущее положение дел и потенциал компании. После составления SWOT-таблицы открывается возможность разрабатывать стратегические планы на качественном уровне.
Однако одного качественного уровня для построения стратегических планов недостаточно. Для повышения ненадежности и оценки планов необходимы определять количественные значения показателей, связанных с информацией SWOT-таблицы.
Переход от описательных параметров к количественным показателям
При формальном описании SWOT-таблицы используются следующие показатели:
-
 Объем продаж (Sales)
Объем продаж (Sales) - Прибыль (Profit)
- Доля рынка (Market share)
- Затраты (Expenses)
- Себестоимость единицы (Unit cost) (1.1)
- Рентабельность (Profitability)
- Денежные потоки (Cash flow)
- Показатели финансовой устойчивости (Creditability).
Значения показателей определяются аналитически и эвристически.
Для построения модели выберем единый показатель, чтобы иметь возможность производить вычисления относительно сопоставимых величин. Это можно сделать благодаря тому, что все показатели (1.1) взаимосвязаны и, при необходимости, по одному из них можно вычислить другие показатели.
Выберем в качестве единого показателя объемы продаж и относительно него построим SWOT-таблицу. При этом сделаем так, чтобы все события и параметры внешней и внутренней среды учитывались относительно их влияния на объемы продаж.
Для Сильных сторон компании для каждого мероприятия найдем соответствующее ожидаемое увеличение продаж (рис. 1). Для Слабых сторон также определим ожидаемый рост продаж, но в результате устранения соответствующих недостатков.
Для факторов внешней среды – Возможностей и Угроз, учитывается влияние событий внешней среды на объемы продаж. Оценки продаж рассчитываются экспертно или статистически в % и записываются в колонку Продажи (1.1). Колонка Затраты пустая, т.к. компания не имеет возможностей изменять влияние внешней среды и, следовательно, не несет затрат.
Измененная таблица SWOT-анализа Табл.1.1.
| Сильные стороны | Мероприятие, направленные на рост сбыта | Затраты | Рост продаж |
| тыс.долл. | тыс.долл. | ||
| Хорошее сервисное обслуживание | Повышение качества сервисного обслуживания | ||
| Увеличение срока гарантийной службы | |||
| Известная продукция | Увеличение объемов существующей рекламы | ||
| Внедрение модификаций существующих моделей | |||
| Доступ к заемным средствам | Увеличение срока кредитования клиентов | ||
| Увеличение объемов кредитования клиентов | |||
| Дешевое сырье | Введение дополнительных скидок | ||
| Низкая себестоимость | Использование купонов | ||
| Большая доля рынка | Увеличение штата отдела продаж для увеличения доли рынка | ||
| Большая дистрибьюторская сеть | Поиск дополнительных дистрибьюторов | ||
| Бесплатная раздача образцов | |||
| Внедрение новых моделей | |||
| Высокая квалификация техперсонала | Улучшение качества продукции | ||
| Удобство произв.мощностей для модернизации | - | - | - |
| Хорошие связи с покупателями/ дистрибьюторами | Организация презентаций | ||
| Участие в специализированных выставках | |||
| Проведение лотерей для покупателей | |||
| Слабые стороны, недостатки | Мероприятия, направленные на рост сбыта | ||
| Устаревшее оборудование | - | - | - |
| Плохая упаковка | Создание новой упаковки | ||
| Недостаточный собственный капитал | - | - | - |
| Низкая рентабельность | - | - | - |
| Низкая квалификация управляющего персонала | Углубленное обучение управленческого персонала маркетингу | ||
| Слабая информированность о рынке | Создание службы оперативного наблюдения за рынком | ||
| Неудачное расположение складов | Открытие новых, более удобных для клиентов складов | ||
| Бесплатная доставка товара | |||
| Неэффективное использование рекламы | Разработка новых рекламных роликов | ||
| Использование рекламы в печатных СМИ | |||
| Использование почтовой рассылки рекламы | |||
| Использование рекламы в Интернет | |||
| Использование наружной рекламы | |||
| Использование рекламы в метро | |||
| Использование наглядной рекламы в местах продаж (POS) | |||
| ИТОГО | |||
| Возможности | Влияние на объем продаж | Изменение объема продаж %% | |
| Малое количество конкурентов | Рост объема продаж за счет захвата доли рынка конкурентов | 10% | |
| Слабость конкурентов | - | ||
| Растущий спрос | Соответствующий рост продаж | 5% | |
| Низкий банковский процент за кредиты | - | ||
| Программа правительственной поддержки | Снижение цены за счет поддержки и соответствующий рост продаж | 6% | |
| Появление новых рыночных сегментов | Рост продаж за счет захвата новых сегментов рынка | 2% | |
| Появление новых рыночных материалов | Рост продаж за счет снижения цены ввиду снижения себестоимости | 8% | |
| Рост продаж за счет улучшения качества продукции | 4% | ||
| Увеличение зарплаты на государственных предприятиях | Рост продаж за счет роста платежеспособного спроса | 6% | |
| Угрозы | Влияние на объем продаж | ||
| Повышение цен на сырье | Падение продаж при росте себестоимости (затрат на материалы) | -4% | |
| Повышение общего уровня зарплаты | Падение продаж при росте себестоимости (затрат на оплату труда) | -2% | |
| Нестабильная политическая ситуация | Падение продаж при введение новых налогов | -5% | |
| Падение продаж при ослаблении ограничений на импорт | -6% | ||
| Падение продаж при уменьшении потребительских расходов | -3% | ||
| Новые разработки иностранных производителей | Падение продаж при появлении товаров нового поколения | -10% | |
| Новая маркетинговая программа конкурентов | Падение продаж за счет перехода покупателей к конкурентам | -5% | |
| Пробуждения у людей старшего возраста | Потеря объема продаж за счет потребительских предубеждений | -2% | |
| Девальвация национальной валюты | Падение продаж за счет снижения платежеспособного спроса | -3% | |
| Дефицит бюджетных средств на зарплату | - | ||
| ИТОГО | 1% |
В построенной SWOT-таблице для готовых к использованию мероприятий указаны количественные значения показателей. Для внутренней среды указаны значения ожидаемых затрат и эффективность от проводимых мероприятий (рост продаж). Для внешней среды указаны только ожидаемые рост или падение объемов продаж (в %). Первоначально количественные значения указывают приблизительно. С течением времени они уточняются.
Проведем анализ противоречий SWOT-таблицы и примем решение, что в прогнозируемом периоде во внешней среде будет иметь место следующий набор событий (табл.1.2).
Окончательные данные по внешней среде Табл.1.2.
| Влияние на объем продаж | Изменение объема продаж %% |
| Рост объема продаж за счет захвата доли рынка конкурентов | 10% |
| Снижение цены за счет поддержки и соответствующий рост продаж | 6% |
| Рост продаж за счет захвата новых сегментов рынка | 2% |
| Рост продаж за счет снижения цены ввиду снижения себестоимости | 8% |
| Рост продаж за счет улучшения качества продукции | 4% |
| Влияние на объем продаж | |
| Падение продаж при введение новых налогов | -5% |
| Падение продаж при ослаблении ограничений на импорт | -6% |
| Падение продаж при уменьшении потребительских расходов | -3% |
| Падение продаж при появлении товаров нового поколения | -10% |
| Падение продаж за счет перехода покупателей к конкурентам | -5% |
| Потеря объема продаж за счет потребительских предубеждений | -2% |
| Падение продаж за счет снижения платежеспособного спроса | -3% |
| ИТОГО | -4% |
Для построения табл.1.1 и 1.2 произведем постановку задачи.
Математическая модель
Дано. Для увеличения сбыта компании имеется набор мероприятий. Для каждого мероприятия известны требуемые затраты и ожидаемая величина роста продаж. Известна доля бюджета компании, которая выделяется на суммарное покрытие затрат.
Требуется найти такой набор мероприятий (стратегию), которой бы при соблюдении ограничений по бюджету приводил бы к максимальному увеличению продаж.
Сформулирована задача сводится к известной «задаче о ранце». Имеется i=1, n предметов (набор мероприятий), каждый из которых имеет объем bi (требуемые затраты) и обладает стоимостью ai (увеличивает продажи). Ранец имеет ограниченный размер.
Введем булеву переменной хi такую, что
хi, если i-й предмет положен в ранец и (1,1)
хi - нет.
Требуется найти такие хi (i=1,n), т.е. набрать такой набор предметов в ранец, чтобы этот набор обладал наибольшей стоимостью, а по размеру не привыкал объем ранца (затраты не превышали ограничение по бюджету – С).
Математически указанная задача записывается в виде
F(x)= aixi max (1.2)
bixi C (1.3)
Задача о ранце относится к оптимизационным задачам дискретного программирования, которые решаются методами линейного программирования с булевыми переменными.
Идея решения методом линейного программирования состоит:
- В обходе вершин многогранника, в которых находятся решения, удовлетворяющие ограничениям (1.1) и (1.3),
- И нахождении вершины с наибольшим (для max)/наименьшим значением целевой функции (1.2).
Для решения рассматриваемой задачи переведем исходные данные задачи в электронную таблицу (ЭТ) Excel, позволяющую производить вычисления. И создадим структуру для решения оптимизационной задачи с помощью пакета Поиск решения.
На рис.1.3 данные SWOT-таблицы представлены в электронной таблице.
Из рис.1.3 видно, что в таблицу включены данные по Внутренней среде:
- Список мероприятий,
- Затраты,
- Ожидаемый рост продаж,
- Отношение a/b (рост продажа/затраты).
Данные по Внешней среде будут учтены позднее, в конце расчетов, как суммарное изменение объема продаж.
1) Найдем 1-е решение поставленной задачи. В качестве первого метода рассмотрим:
- Простое упорядочение мероприятий по убыванию отношения a/b (продажи/затраты) (рис.1.4);
- «укладывание» в ранец мероприятий, начиная с ценных, пока позволяет ограничение по бюджету.
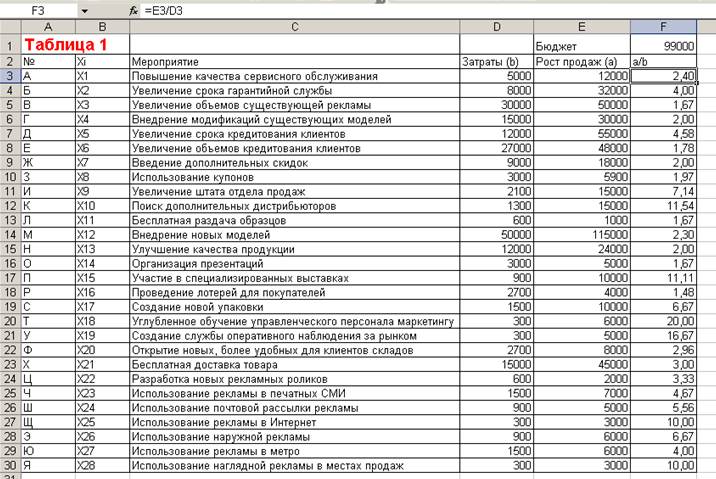 Рис.1.3. Размещенная в электронной таблице SWOT-таблица
Рис.1.3. Размещенная в электронной таблице SWOT-таблица
 Рис. 1.4. Сортировка мероприятий по убыванию относительно a/b
Рис. 1.4. Сортировка мероприятий по убыванию относительно a/b
Рис.1.5. Решение задачи с использованием упорядочивания отношения a/b
 Произведем «укладывание» мероприятий в ранец в порядке убывания отношений a/b (рис.1.4) до заданного ограничения по бюджету 99 000тыс.у.е. (рис.1.5).
Произведем «укладывание» мероприятий в ранец в порядке убывания отношений a/b (рис.1.4) до заданного ограничения по бюджету 99 000тыс.у.е. (рис.1.5).
2. Рассмотрим 2-й метод решения задачи методом линейного целочисленного программирования. Для этого в ЭТ создадим соответствующую структуру данных.

 Рис.1.6. Структуры задачи для решения методом линейного целочисленного
Рис.1.6. Структуры задачи для решения методом линейного целочисленного
программирования

Рис.1.7. Отчет по результатам. Показано найденное решение задачи
На рис.1.7 указано решение целевой функции – 342 000 и оптимальный план мероприятий. Данное решение записано также в ЭТ (рис.1.6).
3. Найдем 3-е решение задачи. Изменим целевую функцию на max S a/b и повторим решение (рис.1.8.)

 Рис.1.8. Отчет по результатам для измененной целевой функции
Рис.1.8. Отчет по результатам для измененной целевой функции
Так как целевая функция S a/b не показывает получаемый доход, то его надо вычислить как сумму произведений доходов от мероприятий на их назначение в план (S aixi) (рис.1.9).
 Рис.1.9. Расчет суммарных доходов для измененной целевой функции.
Рис.1.9. Расчет суммарных доходов для измененной целевой функции.
Для сравнения 3-х методов решений построим график (рис.1.11).

Рис.1.10. сравнение решений по доходам
Из рис.1.10 видно, что наибольший доход дает 2-е решение (метод линейного целочисленного программирования) с целевой функцией, суммирующей доходы.
Оптимальный набор мероприятий для оптимального плана показан на рис.1.11.

Рис. 1.11. Оптимальный план мероприятий