Область локализации корней
Лабораторная работа №11
Тема: Электронная таблица Microsoft Excel.Средства и методы решения уравнений.
Цель работы: Освоить численный метод решения уравнения и встроенные средства решения уравнений..
Содержание
1 Численный метод решения нелинейных уравнений. 1
1.1 Область локализации корней. 1
1.2 Критерии сходимости при решении уравнений. 2
1.3 Метод дихотомии (половинного деления) 3
Пример решения уравнения методом дихотомии. 4
2 Решение уравнений, используя “Подбор параметра”. 6
2.1 Пример решения уравнения, используя “Подбор параметра”. 6
3 Решение уравнений и систем уравнений, используя надстройку “Поиск решения”. 9
3.1 Пример решения уравнения, используя надстройку “Поиск решения”. 10
Задание 1. Решение уравнений численным методом.. 12
Задания 2. Решение уравнений встроенными средствами “Подбор параметра” и “Поиск решения” 12
Контрольные вопросы.. 13
Численный метод решения нелинейных уравнений
Область локализации корней
В общем виде любое уравнение одной переменной принято записывать так  , при этом корнем (решением) называется такое значение x*, что
, при этом корнем (решением) называется такое значение x*, что 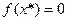 оказывается верным тождеством. Уравнение может иметь один, несколько (включая бесконечное число) или ни одного корня. Как легко видеть, для действительных корней задача отыскания решения уравнения легко интерпретируется графически: корень есть такое значение независимой переменной, при котором происходит пересечение графика функции, стоящей в левой части уравнения f(x), с осью абсцисс.
оказывается верным тождеством. Уравнение может иметь один, несколько (включая бесконечное число) или ни одного корня. Как легко видеть, для действительных корней задача отыскания решения уравнения легко интерпретируется графически: корень есть такое значение независимой переменной, при котором происходит пересечение графика функции, стоящей в левой части уравнения f(x), с осью абсцисс.
Например, для уравнения  выполним преобразование и приведем его к виду f(x)=0 т.е.
выполним преобразование и приведем его к виду f(x)=0 т.е.  . График этой функции представлен на рисунке 1. Очевидно, что данное уравнение имеет два действительных корня – один на отрезке [-1, 0] , а второй – [1, 2].
. График этой функции представлен на рисунке 1. Очевидно, что данное уравнение имеет два действительных корня – один на отрезке [-1, 0] , а второй – [1, 2].

Рисунок 1. График функции 
Таким образом, можно приблизительно определять область локализации корней уравнения. Заметим, что отделить корень можно не единственным образом: если корень отделён на каком-либо отрезке, то годится и любой меньший отрезок, содержащий этот корень. Вообще говоря, чем меньше отрезок, тем лучше, но при этом не следует забывать о том, что на отделение корня на меньших отрезках также тратятся вычислительные усилия, и, быть может, весьма значительные. Таким образом, часто для начала довольствуются весьма широким отрезком, на котором корень отделён.
Некоторые виды уравнений допускают аналитическое решение. Например, степенные алгебраические уравнения степени n  при n ≤ 4. Однако, в общем виде, аналитическое решение, как правило, отсутствует. В этом случае, применяются численные методы. Все численные методы решения уравнений представляют собой итерационные алгоритмы последовательного приближения к корню уравнения. То есть, выбирается начальное приближение к корню x0 и затем с помощью итерационной формулы генерируется последовательность x1, x2, …,xk сходящаяся к корню уравнения
при n ≤ 4. Однако, в общем виде, аналитическое решение, как правило, отсутствует. В этом случае, применяются численные методы. Все численные методы решения уравнений представляют собой итерационные алгоритмы последовательного приближения к корню уравнения. То есть, выбирается начальное приближение к корню x0 и затем с помощью итерационной формулы генерируется последовательность x1, x2, …,xk сходящаяся к корню уравнения  .
.