Графическое отображение вариационных рядов
Вариационный ряд по своей конструкции имеет 2 характеристики:
· значения варьирующего признака – варианты xi, i = 1,2,…,m;
· число случаев вариантов: абсолютные – частоты ni (fi), относительные – частости wi (относительные доли частот в общей сумме частот).
Тогда можно сказать, что вариационный ряд – это ранжированный (упорядоченный) в порядке возрастания или убывания ряд статистических частот (частостей).
Вариационные ряды по способу построения бывают дискретные и интервальные.
Дискретныйвариационный ряд можно рассматривать как такое преобразование ранжированного ряда, при котором перечисляются отдельные значения признака и указывается их частота.
Если число вариантов велико или признак имеет непрерывную вариацию, то строится интервальный вариационный ряд, в котором отдельные варианты объединяются в интервалы (группы). Существуют следующие виды графического отображения вариационных рядов:
· полигон для отображения дискретных рядов, когда фиксируются значения:
( xi; ni, i = 1,2,…,m);
· гистограмма для отображения интервальных рядов:
(ki=х(i+1)–хi, ni(wi));
· кумулята (кумулятивный ряд) – кривая накопленных частот.
Пример.
Построить графическое отображение вариационного ряда. Дано распределение рабочих механического цеха по тарифному разряду:
| Тарифный разряд, хi | Сумма | ||||||
| Количество рабочих (частота), ni | |||||||
| Частость, wi = ni/n | 0,04 | 0,06 | 0,12 | 0,5 | 0,18 | 0,1 |
Данный вариационный ряд является дискретным, его графическое отображение представлено: полигон (на рис. а), кумулята (на рис. б).
 |
а) Дискретный вариационный ряд, (полигон)
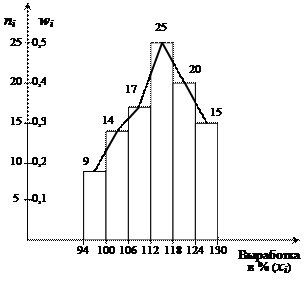 |
б) Интервальный вариационный ряд, (гистограмма, полигон)
Анализ вариационных рядов. Показатели вариации
Вариациейназывается изменяемость, колеблемость величины признака. Вариация проявляется в отклонениях от средних и зависит от множества факторов, влияющих на социально-экономическое явление. Вариация бывает случайной и систематической, существует в пространстве и во времени. Показатели вариации делятся на абсолютные и относительные.
Таблица 5. Показатели вариации
| Показатель | Формула расчета показателя | |
| простой | взвешенный | |
| Абсолютные | Размах | 
|
| Среднее линейное отклонение | 
|  * *
|
| Дисперсия | σ2 
| 
|
| Среднее квадратическое отклонение | 
| 
|
| относительные | Коэффициент вариации | 
|
| Линейный коэффициент вариации | 
| |
| Коэффициент осцилляции | 
|
*– Здесь fi – частота (  ).
).
Ряды динамики
Анализ динамических рядов
Динамический рядпредставляет собой хронологическую последовательность числовых значений статистических показателей.
Виды рядов динамики (РД):
1) моментные (моментальные) РД;
2) интервальные РД;
3) РД с нарастающими итогами;
4) производные РД.
Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени. Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. Пример моментного ряда динамики:
| Дата | 1.01.2001 | 1.04.2001 | 1.07.2001 | 1.10.2001 | 1.01.2002 |
| Число работников, чел. |
Интервальные ряды динамики отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени. Каждый уровень интервального ряда складывается из данных за более короткие интервалы. Пример интервального ряда динамики:
| Год | |||||
| Объем розничного товарооборота, тыс. руб. | 885,7 | 932,6 | 980,1 | 1028,7 | 1088,4 |
Статистическое отображение развития изучаемого явления во времени может быть представлено рядами динамики с нарастающими итогами. Их применение обусловлено потребностями в результатах развития изучаемых показателей не только за данный отчетный период, но и с учетом предшествующих периодов. При составлении таких рядов производится последовательное суммирование смежных уровней. Этим достигается суммарное обобщение результата развития изучаемого показателя с начала отчетного периода (месяца, квартала, года и т.д.).
Производные ряды – ряды, уровни которых представляют собой не непосредственно наблюдаемые значения, а производные величины: средние или относительные.
Основные направления изучения закономерностей развития социально-экономических явлений с помощью рядов динамики:
- характеристика уровней развития изучаемых явлений во времени;
- измерение динамики изучаемых явлений посредством системы статистических показателей;
- выявление и количественная оценка основной тенденции развития (тренда);
- изучение периодических колебаний;
- экстраполяция и прогнозирование.
Таблица 8.1 Уровни (показатели) ряда динамики
| Показатель | Формула | |
| Базисные | Абсолютный прирост | Δ  = yi – у0 = yi – у0
|
| Темп роста | 
| |
| Темп прироста | 
| |
| Цепные | Абсолютный прирост | Δ  = yi – yi-1 = yi – yi-1
|
| Темп роста | 
| |
| Темп прироста | 
| |
| Темп наращивания | 
| |
| Абсолютное значение 1% прироста | 
| |
| Средние | Абсолютный прирост |  = = 
|
| Темп роста |   
| |
| Темп прироста | 
|
Одной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления. На развитие явления во времени оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них оказывают практически постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие же других факторов может быть кратковременным или носить случайный характер.
Основная тенденция (тренд) – изменение, определяющее общее направление развития, это систематическая составляющая долговременного действия, на основе которого можно прогнозировать возможные в будущем значения экономических показателей на основании уже известных.