Теоретические аспекты адаптивных методов прогнозирования
Лабораторная работа 7 - Анализ и прогнозирования временных рядов на основе моделей ARMA
Цели и задачи лабораторной работы
В данной лабораторной работе, на основе динамического ряда денежного агрегата М0 (приложение М) 1 квартал 1999г. по 4 квартал 2005г., рассмотрим способы идентификации и построения ARMA модели, при этом выделим следующие задачи:
1) на основе фактических данных построить авторегрессионную и частную авторегрессионную функцию и сделать предположение о стационарности ряда;
2) с помощью вычисления разностей определить порядок ARMA модели;
3) построить наиболее адекватную имеющимся данным ARMA модель и сделать прогноз на 1-4 квартала 2006г. (сравним полученные результаты с фактическими данными).
Теоретические аспекты адаптивных методов прогнозирования
Основоположниками разработки адаптивных методов можно назвать Дж. Бокса и Г. Дженкенса. Авторы рассматривали так называемые ARMA модели, применение которых основывалось на стационарности исследуемого ряда. В настоящее время круг данных моделей расширен до ARIMA моделей (Авто Регрессия и Проинтегрированное Скользящие Средние) что позволило применять их к более широкому кругу временных рядов из-за снижения требований предъявляемых к исходному денамическому ряду.
В отечественной литературе проблемами построения авторегрессионных моделей посвящены работы Лукашина Ю.П. [ ], Конторовича Г.Г. [ ], Носко В.П. [ ] и Давнис В.В. [ ]. В приведенных работах освещены вопросы, касающиеся описания как одномерных, так и многомерных временных рядов с применением авторегрессионных моделей. Приведены модели развивающие подход Бокса и Дженкенса, допускающие наличие детерминированного или стохастического тренда, структурных изменений и т.д.
Согласно перечисленным работам процесс построения ARIMA моделей можно разбить на несколько этапов:
1 этап. С помощью соответствующих тестов проводят анализ динамического ряда на стационарность. Если в рассматриваемый временной ряд она присутствует, то переходят к третьему этапу построения.
Ряд, для которого выполнены указанные три условия:
- E(yt) ≡ µ - если процесс строго стационарный, то его математическое ожидание не зависит от времени;
- D(yt) ≡ σ2 – дисперсия строго стационарного процесса в каждый момент времени одинакова;
- Cov(yt , yt + τ) = γ(τ) для любых t и τ - автокорреляционная функция стационарного временного ряда зависит только от разности моментов времени (t1-t2).
называют стационарным в широком смысле (слабо стационарным, стационарным второго порядкаили ковариационно стационарным).
2. этап. Если временной ряд не стационарный, то его с помощью соответствующих преобразований можно привести к стационарному.
Во-первых, можно применить d раз взятие разностей. Считается, что с помощью этой процедуры можно исключить тренд составляющую ряда.
Во-вторых, можно оценить линейный (или не линейный) тренд и вычесть его из исходных данных, т.е. 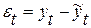 (где
(где  или другая функция).
или другая функция).
3. этап. Если мы предполагаем, что некоторый наблюдаемый временной ряд y1, y2, …, yT порождается моделью ARMA, то при этом возникает проблема подбора конкретной модели из этого класса, решение которой предусматривает три этапа:
1) идентификациямодели;
2) оцениваниемодели;
3) диагностикамодели.
На этапе идентификации производится выбор некоторой частной модели из всего класса ARMA, т.е. выбор значений p и q. при этом можно руководствоваться поведением автокорреляционных и частных автокорреляционных функций (АКФ и ЧАКФ). Опираясь на свойства АКФ и ЧАКФ за годы практической работы с авторегрессионными моделями, исследователями были сформулированы некие правила выбора наилучшей модели, приведенные в работе [дуброва] и представленные таблицей 7.1.
На втором этапе производится уточнение оценок коэффициентов модели с использованием эффективных статистических методов. Для оцененных коэффициентов вычисляются приближенные стандартные ошибки, дающие возможность, при дополнительных предположениях о распределениях случайных величин y1, y2, … , строить доверительные интервалы для этих коэффициентов и проверять гипотезы об их истинных значениях с целью уточнения спецификации модели.
На третьем этапе применяются различные диагностические процедуры проверки адекватности выбранной модели имеющимся данным.
Неадекватности, обнаруженные в процессе такой проверки, могут указать на необходимую корректировку модели, после чего производится новый цикл подбора, и т.д. до тех пор, пока не будет получена удовлетворительная модель.
Таблица 7.1 – Свойство автокорреляционных и частных автокорреляционных функций
| Функции | АКФ | ЧАКФ |
| ARMA(1,0) | Экспоненциально затухает (монотонно или знакопеременно) | Выброс (пик) на лаге 1 |
| ARMA(2,0) | Экспоненциально затухает или имеет форму синусоидальной волны | Выбросы (пики) на лагах 1 и 2 |
| ARMA(0,1) | Выброс (пик) на лаге 1 | Экспоненциально затухает (монотонно или знакопеременно) |
| ARMA(0,2) | Выбросы (пики) на лагах 1 и 2 | Экспоненциально затухает или имеет форму синусоидальной волны |
| ARMA(1,1) | Экспоненциально затухает от значения r(1) (монотонно или знакопеременно) | Экспоненциально убывает от значения rч(1) (монотонно или знакопеременно) |
Рекомендуемая литература
Для лучшего понимания материала изложенного в данной главе необходимо дополнительно проанализировать следующие источники литературы (см. список использованных источников):