В задачу измерений входит не только нахождение самой величины, но также и оценка допущенной при измерениях погрешности
Абсолютная погрешность измерений - погрешность измерений, выраженная в единицах измеряемой величины:
=хизм-х0 . Следует иметь в виду, что поскольку истинное значение измеряемой величины х0 является неизвестным, на практике можно найти лишь некоторую оценку погрешности измерений (с той или иной степенью достоверности).
Относительная погрешность измерений - отношение абсолютной погрешности к истинному значению измеряемой величины ∆х/х0 . Обычно в качестве оценки относительной погрешности принимается отношение абсолютной погрешности к измеренному значению ∆х/хизм. Относительная погрешность выражается в процентах.
Физический измерительный прибор является инструментом для проведения измерений. Функция прибора состоит в воспроизводстве эталона и возможности сравнения его с исследуемым объектом или процессом. Важнейшей характеристикой прибора является максимальная допустимая погрешность. Она определяет собой класс точности прибора.
Класс точности электроизмерительного прибора - выраженное в процентах максимальное значение относительной погрешности прибора, соответствующее пределу измерений:
,
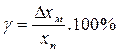где γ – класс точности прибора, ∆хм – максимальная погрешность прибора, хn - предел измерений (максимальное значение физической величины, которое может быть измерено прибором).
Относительная погрешность измерений прибором связана с классом прибора, но в общем случае не совпадает с ним. Она равна:
,
где х - текущее значение измеряемой величины.
Погрешности измерений принято подразделять на грубые,
случайные и систематические.
Грубые погрешности (промахи) возникают вследствие ошибок в снятии отсчетов, неверной записи показаний прибора и тд. Обычно грубые погрешности могут быть легко обнаружены сопоставлением ряда данных.
Случайные погрешности - погрешности, меняющие величину и знак от опыта к опыту. Случайные погрешности имеют различные значения даже для измерений, выполненных одинаковым образом. Случайные погрешности обязаны своим происхождением ряду причин, действие которых неодинаково в каждом опыте и не может быть учтено. Случайные погрешности можно выделить путем сравнения результатов, полученных при нескольких измерениях в одинаковых условиях.
|
Рис.1.Случайные и систематические погрешности:
а – систематической погрешности нет,
б – имеются случайные и систематические погрешности.
Систематические погрешности - погрешности, значение которых одинаково во всех измерениях, проводящихся одним и тем же методом с помощью тех же измерительных приборов. Систематические погрешности могут быть связаны как с ошибками приборов, так и с самой постановкой опытов.
Различие между случайными и систематическими погрешностями иллюстрируется рис. 1.
Случайные погрешности относятся к классу случайных величин - предмету изучения теории вероятности и математической статистики. Ниже приводятся основные правила обращения с такими величинами, вытекающими из строгой теории погрешностей.
Пусть в результате измерений величины х получен ряд значений
x1, х2, х3, ... , хn
свободных от систематической погрешности. Наиболее близким к истинному значению х измеряемой величины х является среднее арифметическое значение
Среднее арифметическое значение <х> обычно принимают в качестве наилучшего значения измеренной величины. Следует иметь в виду, что фактически среднее арифметическое значение является лишь наиболее вероятным значением измеряемой величины.
Погрешность серии из n измерений можно описать понятием средне квадратичной погрешности. Случайная среднеквадратичная погрешность определяется следующим образом:
 |
 |
Понятие среднеквадратичной погрешности применяется для анализа экспериментальных данных в случае, если число измерений достаточно велико (во всяком случае, не меньше чем 4-5).
Систематические погрешности определения физических величин связаны с используемыми методами измерений и приборами. Анализ систематических погрешностей, вытекающих из методики эксперимента, может быть весьма сложен и выполняется отдельно для каждой методики. Систематические погрешности, связанные с используемыми приборами, определяются их классом точности. Класс точности определяет максимальную погрешность измерений. Среднеквадратичная же погрешность дает лишь некоторую оценку отклонения результата от истинного значения. Чтобы оценить среднеквадратичную погрешность измерений прибором, следует максимальную допустимую погрешность прибора разделить на два (для электроизмерительных приборов - класс точности прибора разделить на два).
Реально в экспериментах одновременно присутствуют случайные и систематические погрешности. Пусть они характеризуются среднеквадратичными погрешностями σслуч и σсист.
Полная среднеквадратичная погрешность измерений находится по формуле
 |
 |
Результат физических измерений принято записывать в виде
 |
Пример обработки результатов измерений
Измерялась плотность образца из органического стекла. Образец имел форму параллелепипеда. Для нахождения плотности проведены измерения массы образца и его линейных размеров. Масса m определялась на технических весах (цена деления – 50 мг), линейные размеры a, b, c измерялись линейкой (цена деления - 1мм). Результаты измерений представлены в таблице 2
Таблица 2
| N | m, г | a, мм | b, мм | c, мм |
| 2.895 | 18.5 | 11.5 | ||
| 2.839 | 18.5 | 11.5 | ||
| 2.910 | 18.5 | 11.0 | ||
| 2.852 | 18.5 | 11.5 | ||
| 2.870 | 18.0 | 11.0 | ||
| 2.925 | 18.5 | 11.5 | ||
| 2.820 | 18.0 | 11.0 | ||
| 2.865 | 18.5 | 11.0 |
По результатам измерений находим средние значения измеряемых величин:
, <x>=2.873, <a>=18.4, <b>=12, <c>=11.25
и случайные среднеквадратичные погрешности
,
, 
, 
Систематические погрешности измерений можно оценить как половину допустимой погрешности приборов
, 
, 
Полные погрешности 
,
σm =0.027, σa =0.51, σb = 0.5, σc=0.51
Таким образом, средние значения объема и плотности равны
<V>=<a><b><c>=2.48 см3
<ρ>=<m>/<V>=1.16 г/см3
Далее, на основании таблицы 1, находим средне-квадратичную погрешность определения плотности
= 
= 
,
= 
=0.09 г/см3
Таким образом, плотность исследуемого образца составляет
Основную погрешность в измерение плотности, в данном случае, вносит систематическая погрешность определения линейных размеров.
Составление отчета
Отчет о выполненной лабораторной работе составляется в письменном виде (желательно в специальной тетради). В нем должны быть отражены следующие основные моменты проведенного экспериментального исследования:
1. Наименование работы, фамилии учащихся, дата выполнения
работы.
2. Цель работы, используемые приборы и оборудование.
3. Метод и схема измерений.
4. Таблицы полученных экспериментальных данных
(обязательно приводить результаты первичных измерений).
5. Результаты обработки измерений вместе с анализом
погрешностей.
6. Особенности и ограничения используемого метода
измерений.
7. Выводы.
ОТВЕТЬТЕ НА ВОПРОСЫ
1) Чем ограничивается точность измерений?
2) Каковы пути повышения точности?
Лабораторная работа №2