Абсолютно упругий центральный удар.
ЛАБОРАТОРНАЯ РАБОТА № 4
ЗАКОНЫ СОХРАНЕНИЯ
| Цель работы:экспериментальное исследование процесса соударения упругих тел и проверка выполнения в | |||||
| системе соударяющихся тел законов сохранения импульса и энергии. | |||||
| Теория. Основные понятия и определения. | |||||
| Импульс – векторная физическая величина, являющаяся механической мерой движения тела, равная произведению | |||||
| массы этого тела на его скорость. | |||||
| Закон сохранения импульса – векторная сумма импульсов всех тел системы есть величина постоянная, если | |||||
| векторная сумма внешних сил, действующих на систему тел равна нулю. | |||||
| Энергия – скалярная физическая величина, являющаяся мерой различных форм движения и взаимод. материи. | |||||
| Кинетическая энергия – скалярная функция, являющаяся мерой движения материальной точки и зависящая | |||||
| только от массы и модуля скорости материальных точек, образующих рассматриваемую физическую систему. | |||||
| Потенциальная энергия – скалярная физическая величина, представляющая собой часть полной механической | |||||
| энергии системы, находящейся в поле консервативных сил. | |||||
| Внутренняя энергия – энергия покоя, складывающаяся из теплового хаотического движения молекул, | |||||
| составляющих тело, потенциальной энергии их расположения, кинетической и потенциальной энергии | |||||
| электронов в атомах, нуклонов в ядрах и так далее. | |||||
| Закон сохранения энергии – сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему | |||||
| и взаимодействующих друг с другом посредством сил тяготения и упругости, остается неизменной. | |||||
| Удар (или соударение) – кратковременное взаимодействие тел, при котором происходит перераспределение | |||||
| кинетической энергии. | |||||
| Центральный удар – удар, при котором линия, соединяющая центры взаимодействующих тел, лежит на линии | |||||
| их движения. | |||||
| Абсолютно упругий удар – модель соударения, при котором полная кинетическая энергия системы сохраняется. | |||||
| Считается, что энергия на деформации не теряется, и взаимодействие распространяется по телу мгновенно. | |||||
| Для математического описания простейших абсолютно упругих ударов используется закон сохранения энергии и | |||||
| закон сохранения импульса. | |||||
| Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются и двигаются дальше | |||||
| как единое целое. | |||||
| Абсолютно упругий нецентральный удар – модель соударения тел, при котором полная кинетическая энергия | |||||
| системы сохраняется, энергия не тратится на деформацию тел и взаимодействие распространяется по телам | |||||

| системы мгновенно, при этом линия, соединяющая центры | ||||
| взаимодействующих тел, лежит на лини их движения. | |||||
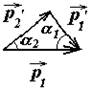
| |||||

| |||||

| |||||

| |||||
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с работой программы “Законы сохранения”.
2. Изучить на примере соударения двух шаров абсолютно упругий центральный удар. Для этого задать значение коэффициента упругости k = 1 (упругий удар) и значение прицельного расстояния d равным нулю.
3. Задавая начальные параметры в соответствии с вариантами исходных данных, провести эксперимент для различных соотношений масс сталкивающихся шаров. Данные занести в таблицу 1.
Таблица 1
| 1. Соотношение масс шаров: m1 = m2 | Параметры первого шара | Параметры второго шара |
| m1 = 3 | m2 = 3 | |
| До удара | V1 = 9 | V2 = 0 |
| После удара |  0 0
|  9 9
|
| 2. Соотношение масс шаров: m1 > m2 | m1 = 3 | m2 = 2 |
| До удара | V1 = 9 | V2 = 0 |
| После удара |  1,8 1,8
|  10,8 10,8
|
| 3. Соотношение масс шаров: m1 < m2 | m1 = 1 | m2 = 3 |
| До удара | V1 = 9 | V2 = 0 |
| После удара |  -4,5 -4,5
|  4,5 4,5
|
4. Изучить на примере соударения двух шаров абсолютно упругий нецентральный удар. Для этого задать значение коэффициента упругости k = 1 (упругий удар) и значение прицельного расстояния d, в соответствии с вариантами не равное нулю.
5. Задавая начальные параметры в соответствии с вариантом (стр. 65 - 66, таблицы 1 - 3), провести эксперимент для различных соотношений масс сталкивающихся шаров. Результаты измерений занести в таблицу 2.
Таблица 2
| 1. Соотношение масс шаров: m1 = m2 | Параметры первого шара | Параметры второго шара |
| m1 = 1,5 | m2 = 1,5 | |
| До удара | V1 = 7 | V2 = 0 |
| После удара |  42 42
|  48 48
|
 -5,22 -5,22
|  4,66 4,66
| |
| 2. Соотношение масс шаров: m1 > m2 | m1 = 1,5 | m2 = 0,5 |
| До удара | V1 = 7 | V2 = 0 |
| После удара |  17 17
|  48 48
|
 5,72 5,72
|  7 7
| |
| 3. Соотношение масс шаров: m1 < m2 | m1 = 1,5 | m2 = 4,5 |
| До удара | V1 = 7 | V2 = 0 |
| После удара |  115 115
|  48 48
|
 -5,72 -5,72
|  2,33 2,33
|
6. На примере соударения двух шаров изучить абсолютно неупругий центральный удар. Для этого задать значение коэффициента упругости k = 0 (неупругий удар) и значение прицельного расстояния d равным нулю.
7. Задавая начальные параметры в соответствии с вариантом (стр. 65 - 66, таблицы 1 - 3), провести эксперимент для различных соотношений масс сталкивающихся шаров. Данные занести в таблицу 3.
Таблица 3
| 4. Соотношение масс шаров: m1 = m2 | Параметры первого шара | Параметры второго шара |
| m1 = 0,5 | m2 = 0,5 | |
| До удара | V1 = 5 | V2 = 0 |
| После удара |  2,5 2,5
|  2,5 2,5
|
| 5. Соотношение масс шаров: m1 > m2 | m1 = 3 | m2 = 0,5 |
| До удара | V1 = 5 | V2 = 0 |
| После удара |  4,29 4,29
|  4,29 4,29
|
| 6. Соотношение масс шаров: m1 < m2 | m1 = 0,5 | m2 = 4,5 |
| До удара | V1 = 5 | V2 = 0 |
| После удара |  0,5 0,5
|  0,5 0,5
|
8. Используя данные таблицы 1, рассчитать значения импульсов и кинетической энергии шаров после абсолютно упругого центрального удара.
9. Найти суммарный импульс и суммарную кинетическую энергию системы шаров до и после абсолютно упругого центрального удара. Для каждого эксперимента сделать выводы о выполнении законов сохранения импульса и энергии для абсолютно упругого центрального удара.
10. Используя данные таблицы 2, рассчитать значения импульсов и кинетической энергии шаров после абсолютно упругого нецентрального удара.
11. Используя данные расчетов п.10 и таблицы 2, построить в выбранном масштабе векторные диаграммы импульсов и найти суммарную кинетическую энергию системы шаров до и после абсолютно упругого нецентрального удара. Для каждого эксперимента сделать выводы о выполнении законов сохранения импульса и энергии для абсолютно упругого нецентрального удара.
12. Используя данные таблицы 3, рассчитать значения импульсов и кинетической энергии шаров после абсолютно неупругого центрального удара.
13. Найти суммарный импульс, суммарную кинетическую энергию системы шаров до и после абсолютно неупругого центрального удара. Найти изменение внутренней энергии системы шаров. Для каждого эксперимента сделать выводы о выполнении законов сохранения импульса и энергии для абсолютно неупругого центрального удара.
14. Сделать вывод о выполнении законов сохранения импульса и энергии для упругого и неупругого ударов.
15. Ответить на контрольные вопросы.
ОТЧЕТ
Абсолютно упругий центральный удар.
1. Соотношение масс шаров: m1 = m2








| Вывод: |
2. Соотношение масс шаров: m1 > m2








| Вывод: |
3. Соотношение масс шаров: m1 < m2







