Требования к оформлению решений математических задач
Общие требования культуры ведения записей
В экзаменационной работе
1. Краткое условие задачи (если оно есть в геометрических задачах) отделяется от решения.
2. Всякая новая мысль начинается с красной строки.
3. Записи ведутся аккуратно, разборчивым подчерком, используя
шариковую ручку с пастой синего или фиолетового цвета.
4. Не допускается использование фломастеров, наклеек, цветных
стержней.
5. Между номером задания, решением и ответом пропускается одна
клетка вниз.
6. Построение геометрических фигур, графиков функций, выполнение рисунков осуществляется только с помощью карандаша, линейки и циркуля. Элипсообразные фигуры с помощью шаблона.
7. Правильное расположение математических знаков в строке. Так, перенос формулы или выражения с одной строки на другую разрешается производить только на знаках сложения, вычитания, умножения и равенства. При переносе, знаки «+», «-» и «=» повторяются на следующей строке, знак умножения заменяется «х», который тоже повторяется на следующей строке. Правильно располагать черту дроби и знак равенства. Черта дроби не разрывается.
8. Сокращение обозначений единиц измерения должно быть правильным.
9. Не допустимо сокращение слов в рассуждениях.
10. Сильно не увлекаться использованием математической символики.
11. Нельзя слова «следовательно», «значит», «треугольник», «параллельно» и т.д. в тексте заменять математическими знаками.
12. В конце решения должен быть обязательно ответ. В задачах на доказательство, исследование или построение – вывод.
Требования к оформлению решений математических задач
1. Правильность решения. Решение задачи не должно содержать математических и логических ошибок. Среди математических ошибок различают существенные (грубые) и несущественные (негрубые) ошибки.
Вопрос о том, ккакого рода ошибкам (существенным или несущественным) относится та или иная ошибка, является довольно сложным и спорным и его следует внимательно рассматривать в каждом отдельном случае. Деление погрешностей на ошибки и недочеты является условным, и учитель должен учитывать то, что размытость границ между негрубой ошибкой и недочетом, грубой и негрубой ошибками, а порой даже между грубой ошибкой и недочетом может быть причиной необъективной оценки.
Вообще, при проверке работ следует иметь в виду, что оформление решений может быть разным. Здесь важно, чтобы в записях были видны основные этапы решения и логика. Не следует стремиться к «идеальному» эталону оформления. Не следует требовать от учащихся излишне развернутых обоснований. Надо обосновывать все то, что не является очевидным по ходу решения и объяснять дополнительные построения, если они выполняются.
При оценке результатов учебной деятельности учащихся учитывается характер допущенных ошибок: существенных и несущественных.
К существенным (грубым) ошибкамотносятся ошибки, свидетельствующие о том, что ученик не знает формул, не усвоил математические понятия, правила, утверждения, не умеет оперировать ими и применять к выполнению заданий и решению задач.
А именно:
а) незнание, непонимание определений основных математических понятий, формулировок теорем, формул, которые предусмотрены программой,
б) незнание сущности математических понятий, математических величин,
в) неумение решать простейшие задания,
г) неумение строить графики элементарных функций,
д ) неправильное применение методов, способов, приемов решения
практических заданий.
Примеры:
1) 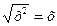 ,
,
2) х 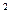
 9, х
9, х  3 и х
3 и х  -3.
-3.
3) sin 2  = 2 sin
= 2 sin 
4)sin(-30) = -sin 30
5)
К несущественным (негрубым) ошибкамотносятся ошибки, свидетельствующие о недостаточно полном или недостаточно прочном усвоении знаний и умений или об отсутствии знаний, не считающихся по программе основными, т.е. отдельные ошибки вычислительного характера, погрешности в формулировке вопросов, определений, математических утверждений, небрежное выполнение записей, рисунков, графиков, схем, диаграмм, таблиц, а также грамматические ошибки в написании математических терминов. Такого рода ошибки не приводят к искажению смысла задания и его выполнения и не влияют на ответ.
Например:
1) неточность определений, формулировок, теорем, формул;
2)недостаточное обоснование существенных утверждений решения;
3) исключение без объяснения одного из корней уравнения;
4) построение графика линейной функции по трем точкам;
5) в окончательном ответе не избавились от иррациональности в знаменателе;
6) запись ответа в виде сократимой дроби;
7) небрежность и неаккуратность записей, рисунков, чертежей;
8) стилистические, пунктуационные и орфографические ошибки;
9) запись ответа в виде сократимой дроби;
10) исключение без объяснениякорня уравнения;
11) изображение отрезка, концами которого являются штрихи;
12) график линейной функции построен по трем и более точкам;
13) ответ представлен в виде сократимой дроби;
14) решение неравенства записано в виде х  (0; 8);
(0; 8);
15) запись: функция возрастает на (1; 2)  (7;
(7;  );
);
16) разорвана черта дроби;
17) различные единичные отрезки на осях координат;
18) невидимые линии в сечении и изображении фигур нарисованы сплошной линией.
Логические ошибки– это ошибки в рассуждениях и доказательствах, вызванные нарушением правил и законов логики. Они чаще всего обусловлены неправильным употреблением логических связок «и», «или», «если…, то…», недостаточным осознанием понятий «логическое следование», «логическая равносильность», нечетким пониманием идеи доказательства методом от противного и т.д.
В любой геометрической задаче обязательна краткая запись условия либо словесное введение условия в решение. В большинстве геометрических задач требуется рисунок. Изображение фигуры считается верным, если оно дает однозначное представление о фигуре и позволяет выполнять дополнительные построения.
2. Обоснованность решения. Пояснительный текст, сопровождающий решение, должен содержать ссылки на аксиомы, теоремы, следствия. Отсутствие обоснований может привести к неверным результатам. Однако важно уметь отличать существенное от несущественного при записи пояснительного текста. Например, нет необходимости пояснять, что обе части уравнения возводятся в квадрат, записывать в общем виде формулы корней квадратного уравнения, тригонометрические тождества и т.д. Но должны быть обоснованы отброшенные корни, отсутствие корней, взаимное расположение прямых, построение линейного угла в двугранном угле, расположение основания высоты в пирамиде, положение и форма граней, угол между прямой и плоскостью, расстояние между скрещивающимися прямыми и т.д. Другими словами надо обосновывать все то, что не является очевидным по ходу решения задачи, и объяснять дополнительные построения, если они производились.
3. Полнота решения. При решении математической задачи должны быть рассмотрены все возможные случаи, если это предполагает условие. Неполнота решения является существенным недостатком при решении задачи.
Например:
Если в равнобедренном треугольнике угол 44°, то он может быть и при вершине, и при основании.
4.Рациональность решения. Если задача допускает несколько способов решения и с ними знаком ученик, то весьма желательно, чтобы приводилось рациональное решение.
5.Соблюдение правил правописания. Решение математической задачи не должно содержать орфографических, пунктуационных и речевых ошибок. Если они присутствуют, то они должны исправляться учителем.
При оценивании экзаменационных работ учитывается характер допущенных существенных и несущественных ошибок. Количество баллов за выполнение задания снижается на 10 %, если в нем допущена несущественная ошибка. Если при выполнении задания допущена существенная ошибка, то задание считается невыполненным.