Основная теорема о взаимосвязи полосы пропускания канала и скорости передачи данных.
Любой сигнал можно рассматривать как функцию времени, или как функцию частоты. В первом случае эта функция показывает, как меняются впоследствии параметры сигнала, например, напряжение или ток. Если эта функция имеет непрерывный характер, то говорят о непрерывном сигнале. Если эта функция имеет дискретный вид, то говорят одискретном сигнале.
Частотное представление функции основано на том факте, что любая функция может быть представлена в виде ряда Фурье
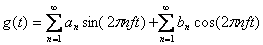
 (1),
(1),
где  - частота, an,bn –амплитуды n-ой гармоники.
- частота, an,bn –амплитуды n-ой гармоники.
Характеристику канала, который определяет спектр частот, которые физическая среда, из которой сделана линия связи, которая образует канал, пропускает без существенного снижения мощности сигнала, называют полосой пропускания.
Максимальную скорость, из которой канал способен передавать данные, называютпропускной способностью канала или битовой скоростью.
В 1924 Найквист открыл взаимосвязь между пропускной здатностью канала и шириной его полосы пропускания.
Теорема Найквиста
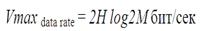
где  – максимальная скорость передачи H -ширина полосы пропускания канала, выраженная в Гц, М- количество уровней сигнала, которые используются при передаче. Например, из этой формулы видно, что канал с полосой 3 кГц не может передавать двухуровневые сигналы быстрее 6000 бит/сек.
– максимальная скорость передачи H -ширина полосы пропускания канала, выраженная в Гц, М- количество уровней сигнала, которые используются при передаче. Например, из этой формулы видно, что канал с полосой 3 кГц не может передавать двухуровневые сигналы быстрее 6000 бит/сек.
Эта теорема также показывает, что, например, бессмысленно сканировать линию чаще, чем удвоена ширина полосы пропускания. Действительно, все частоты выше этой отсутствуют в сигнале, а потому вся информация, необходимая для возобновления сигнала будет собрана при таком сканировании.
Однако, теорема Найквиста не учитывает шум в канале, который измеряется как отношение мощности полезного сигнала к мощности шума: S/N. Эта величина измеряется в децибелах: 10log10(S/N) dB. Например, если отношение S/Nравняется 10, то говорят о шуме в 10 dB если отношение равняется 100, то - 20 dB.
На случай канала с шумом есть теорема Шенона, по которой максимальная скорость передачи данные по каналу с шумом равняется:
H log2 (1+S/N)бит/сек, где S/N -соотношение сигнал-шум в канале.
Здесь уже не важно количество уровней в сигнале. Эта формула устанавливает теоретический предел, который редко достигается на практике. Например, по каналу с полосой пропускания в 3000 Гц и уровнем шума 30 dB (это характеристики телефонной линии) нельзя передать данные быстрее, чем со скоростью 30 000 бит/сек.
Теорема Шеннона — Хартли
В данной теореме определено, что достичь максимальной скорости (бит/с) можно путем увеличения полосы пропускания и мощности сигнала и, в то же время, уменьшения шума.
Теорема Шеннона — Хартли ограничивает информационную скорость (бит/с) для заданной полосы пропускания и отношения «сигнал/шум». Для увеличения скорости необходимо увеличить уровень полезного сигнала, по отношению к уровню шума.
Если бы существовала бесконечная полоса пропускания, бесшумовой аналоговый канал, то можно было бы передать неограниченное количество безошибочных данных по ней за единицу времени. Реальные каналы имеют ограниченные размеры и в них всегда присутствует шум.
Удивительно, но не только ограничения полосы пропускания влияют на количество передаваемой информации. Если мы комбинируем шум и ограничения полосы пропускания, мы действительно видим, что есть предел количества информации, которую можно было передать, даже используя многоуровневые методы кодирования. В канале, который рассматривает теорема Шеннона — Хартли, шум и сигнал дополняют друг друга. Таким образом, приёмник воспринимает сигнал, который равен сумме сигналов, кодирующего нужную информацию и непрерывную случайную, которая представляет шум.
Это дополнение создает неуверенность относительно ценности оригинального сигнала. Если приёмник обладает информацией о вероятности ненужного сигнала, который создает шум, то можно восстановить информацию в оригинальном виде, рассматривая все возможные влияния шумового процесса. В случае теоремы Шеннона — Хартли шум, как таковой, произведен гауссовским процессом с некоторыми отклонениями в канале передачи. Такой канал называют совокупным белым гауссовским шумовым каналом, так как гауссовский шум является частью полезного сигнала. «Белый» подразумевает равное количество шума во всех частотах в пределах полосы пропускания канала. Такой шум может возникнуть при воздействии случайных источников энергии, а также быть связан с ошибками, возникшими при кодировании. Зная о вероятности возникновения гауссовского шума, значительно упрощается определение полезного сигнала.