Раскроем модель определения результатов тестирования
Вариант 4.
Часть 1.
1. Выполните форматирование нижеприведенного документа «Системы тестирования знаний» с учетом следующих параметров форматирования:
- красная строка – 1.25 см;
- выравнивание по ширине (основной текст), заголовки по центру;
- размер шрифта – 14 пт, заголовки – 16 пт;
- начертание шрифта Times New Roman, обычный;
- отступы слева и справа – 0;
- междустрочный интервал – одинарный;
- межзнаковый интервал – обычный;
- на все таблицы в тексте должны быть ссылки. Таблица должна располагаться непосредственно после текста, в котором она упоминается впервые, или на следующей странице. Все таблицы нумеруются (нумерация сквозная), например: Таблица 3 - Доходы фирмы;
- все формулы нумеруются. Нумерация сквозная. Номер проставляется арабскими цифрами в круглых скобках в крайнем правом положении на строке, например,
А = а:b (1)
- номер параграфа состоит из номеров главы и параграфа в главе, разделенных точкой. В конце номера точка не ставится. Аналогичным образом нумеруются и пункты в параграфе (например: 2.4.2 Анализ результатов).
- включив кнопку «Отобразить все знаки», проверьте наличие одного пробела между словами в предложениях и отсутствие знака «перенос строки».
2. Добавьте титульный лист, содержащий название учебного заведения, название документа, ФИО автора;
3. Вставьте нумерацию страниц на всех листах документа, кроме первого. Пронумеруйте соответствующие формулы в тексте документа;
4. Выполните форматирование таблиц определенным стилем;
5. Оформите заголовки стилями Заголовок 1, Заголовок 2, Заголовок 3 и создайте оглавление (автоматически собираемое с нумерацией страниц) на втором листе документа, в соответствии с нижеприведенным шаблоном:
1 Системы тестирования знаний
1.1 Порядок проверки надежности, дискриминативности, валидности разработанных тестов
1.2 Примерный вид матрицы интеркорреляций, вычисляемой для подтверждения внутренней согласованности теста
1.2.1 Механизм определения эффективности обучения на основе статистической модели
1.2.2 Разработка и реализация целостного учебного процесса в технологии дистанционного обучения
Список литературы
Текст:
Системы тестирования знаний
Сформулируем критерии формирования системы тестирования знаний :
1) Система тестирования знаний должна включать в себя две необходимых составляющих:
- подсистему подготовки тестов (редактор тестов);
- собственно программу тестирования.
2) Подсистема подготовки тестов является инструментом, позволяющим создать новый тест по разделу курса из соответствующих вопросов, добавить его к перечню имеющихся тестов по соответствующим разделам соответствующих дисциплин, при необходимости отредактировать параметры теста и содержание его вопросов и задач.
3) Подсистема тестирования должна обеспечивать выбор теста по соответствующему разделу соответствующего курса из числа имеющихся в перечне; выбор студента, которому назначается данный тест; собственно проведение теста; обработку, представление и хранение результатов теста.
Раскроем модель определения результатов тестирования
Результаты теста оцениваются в процентном отношении числа правильных ответов к общему числу вопросов. Если все ответы теста правильные, то результатом теста является 100 % .
В приведенной ниже модели определения результатов теста используются следующие переменные:
i - номер задачи;
n - число задач;
R - результат теста (0¸100 %);
a[i] - (массив) результат ответа на i-й вопрос;
a[i]=0 - ответ неверный;
a[i]=1 - ответ верный;
W[i] - весовой коэффициент i-го вопроса или задачи.
Если вопросы или задачи неравнозначны, то весовые коэффициенты могут иметь разные значения для разных задач и находиться в определенном диапазоне значений, например, W[i]=1…10.
Для каждого вопроса должен быть определен нормализованный весовой коэффициент, приводящий результаты теста к единому результирующему максимально возможному уровню в 100 % .
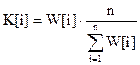
В случае многовариантных ответов с несколькими правильными ответами вводятся переменные:
j - номер ответа многовариантной задачи;
m - число ответов многовариантной задачи;
b[i,j] - j-й вариант ответа на i-й вопрос;
b[i,j]= 0 - неверный вариант ответа.
В данном случае неверным вариантом ответа является, как выбор неверного ответа, так и невыбор верного варианта.
b[i,j]=1 - верный вариант ответа.
Тогда результат ответа на i-й вопрос:
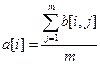
В случае, если выбраны не все правильные ответы, результат ответа a[i] получается меньше 1. В случае выбора всех возможных вариантов ответа результат ответа получается хуже (меньше), чем при выборе только правильных вариантов.
Результат теста определяется по формуле:

Порядок проверки надежности, дискриминативности, валидности разработанных тестов
Для того чтобы оценки результатов тестов были корректными, следует провести на основании полученных статистических результатов анализ пригодности данного теста вообще для оценки знаний студентов, а также оценить статистическую значимость своего заключения.
Прежде всего следует оценить дискриминативность отдельных тестовых заданий: способно ли каждое из них разделить обучаемых на тех, кто даст правильный ответ, и на тех, кто ответит неверно. В процессе такой оценки для каждого задания необходимо вычислить коэффициенты сложности - Кс. Коэффициент сложности Кс - это отношение количества студентов в каждой группе, не решивших данное задание Nн, к общему количеству испытуемых в данной группе N:
Кс = Nн / N .
Допустим, что пяти группам студентов предлагался тест из 10 заданий и получены следующие оценки математических ожиданий коэффициентов трудности
Кроме того, в нашем примере задания 1-2 существенно уступают по сложности остальным заданиям и, как правило, у большинства студентов их решение не вызывают затруднений. Если таких заданий в тесте будет много, то, возможно, окажется целесообразным выделить их в отдельную группу "легких заданий", разделив таким образом задания теста на два блока по сложности, и реализовать алгоритм адаптивного тестирования.
Таблица .
Оценка средних коэффициентов трудности заданий по группам
| Группы | Номера тестовых заданий | |||||||||
| № 1 | 0,00 | 0,05 | 0,19 | 0,10 | 0,45 | 0,36 | 0,48 | 0,35 | 0,45 | 1,00 |
| №2 | 0,06 | 0,08 | 0,30 | 0,32 | 0,42 | 0,30 | 0,45 | 0,40 | 0,40 | 1,00 |
| №3 | 0,03 | 0,05 | 0,25 | 0,28 | 0,36 | 0,20 | 0,40 | 0,17 | 0,45 | 1,00 |
| №4 | 0,07 | 0,12 | 0,32 | 0,30 | 0,50 | 0,43 | 0,55 | 0,38 | 0,49 | 1,00 |
| №5 | 0,05 | 0,15 | 0,30 | 0,35 | 0,48 | 0,48 | 0,64 | 0,35 | 0,41 | 1,00 |
По мере накопления статистических данных составы "легкого" и "трудного" блоков заданий могут уточняться. Например, задание из "легкого" блока, статистика результатов выполнения которого окажется неудовлетворительной, должно быть переведено в "трудный" блок. Процедура подобного статистического анализа и гибкое изменение состава блоков теста также эффективно может быть реализована на компьютере и фактически является составной частью индивидуально ориентированного алгоритма тестирования.
Дискриминативность теста в целом оценивается показателем, который называется d Фергюсона [101] и отражает количество совпадений результатов испытуемых в выборке:

где N - количество испытуемых в выборке; n - количество заданий;
fk - количество испытуемых, показавших при тестировании k- ий результат
Размерность матрицы интеркорреляций составит (n+1)х(n+1), она симметрична, все ее диагональные элементы равны единице (поскольку соответствует коэффициенту корреляции выборки с самой собой). Вид ее иллюстрируется в таблице .
Все элементы матрицы интеркорреляций должны быть положительными. Подтверждение статистической значимости наличия положительной корреляции осуществляется тем же образом, что и при подтверждении ретестовой надежности.
Таблица .
Примерный вид матрицы интеркорреляций, вычисляемой для подтверждения внутренней согласованности теста
| № заданий | Коэффициенты корреляции между заданиями теста ) | Результат целом | |||||||||
| по тесту в целом | |||||||||||
| 1,00 | 0,69 | 0,48 | 0,29 | 0,37 | 0,35 | 0,38 | 0,25 | 0,17 | 0,07 | 0,16 | |
| 0,69 | 1,00 | 0,54 | 0,43 | 0,31 | 0,30 | 0.41 | 0,30 | 0,22 | 0,07 | 0,22 | |
| 0,48 | 0,54 | 1,00 | 0,65 | 0,45 | 0,40 | 0,45 | 0,32 | 0,16 | 0,20 | 0,37 | |
| 0,29 | 0,43 | 0,65 | 1,00 | 0,32 | 0,24 | 0,44 | 0,37 | 0,35 | 0,45 | 0,42 | |
| 0,37 | 0,31 | 0,45 | 0,32 | 1,00 | 0,61 | 0,25 | 0,24 | 0,31 | 0,17 | 0,26 | |
| 0,35 | 0,30 | 0,40 | 0,24 | 0,61 | 1,00 | 0,35 | 0,46 | 0,14 | 0,18 | 0,23 | |
| 0,38 | 0,41 | 0,45 | 0,44 | 0,25 | 0,35 | 1,00 | 0,24 | 0,14 | 0,17 | 0,07 | |
| 0,25 | 0,30 | 0,32 | 0,37 | 0,24 | 0,46 | 0,24 | 1,00 | 0,55 | 0,35 | 0,18 | |
| 0,17 | 0,22 | 0,16 | 0,35 | 0,31 | 0,14 | 0.14 | 0,55 | 1,00 | 0,42 | 0,23 | |
| 0,07 | 0,07 | 0,20 | 0,45 | 0,17 | 0,18 | 0,17 | 0,35 | 0,42 | 1,00 | 0,12 | |
| Результат пo тесту в целом | 0,16 | 0,22 | 0,37 | 0,42 | 0,26 | 0,23 | 0,07 | 0,18 | 0,23 | 0,12 | 1,00 |
Как видно из характера рассмотренных выше показателей, подтвердить надежность при адаптивном тестировании весьма проблематично, ибо каждому студенту могут "достаться" разные наборы тестовых заданий, и даже одному и тому же студенту во второй раз скорее всего будут предъявлены различные серии заданий.
Механизм определения эффективности обучения на основе статистической модели.
Обозначим наиболее существенные аспекты, связанные с проблематикой данного исследования, отраженные в современных документах, описывающих перспективы и пути развития системы среднего профессионального образования. Одной из областей, предопределяющих успешность этого процесса, называется проработка научного обеспечения системы среднего профессионального образования и в части развития прогнозирования, мониторинга и государственного регулирования подготовки специалистов среднего звена, развития методологии оценки качества образования, подготовки специалистов и методологии оценки эффективности деятельности учреждений СПО.
Описанная таким образом база знаний откроет дополнительные возможности для реализации информационно-ориентированной модели определения эффективности обучения по сравнению с традиционной схемой обучение и контроля. Приведем некоторые из таких возможностей:
1) если при формировании содержания обучения в компьютерной технологии обучения какой-либо параметр или описание опущены преподавателем, то модель определения эффективности обучения должна такое описание создавать автоматически по заложенным в систему формирования содержания соответствующим алгоритмам, которые опираются на критерий аналогичного описания аналогичных элементов;
2) если при контроле для определения уровня усвоения по ряду учебных элементов потребуется больше вопросов, чем задано при описании учебного содержания, то в модель определения эффективности обучения должна действовать система формирования содержания, которая сформирует необходимое количество различных вопросов, исходя из типовой принадлежности учебного элемента и описания его связей с другими учебными элементами.
Руководствуясь общими правилами теории исследования операций и теории массового обслуживания, составим дифференциальные уравнения для вероятностей состояний:

Подставив в первое уравнение системы значение р1 из выражения, имеем

Это уравнение решается при начальных условиях:
р0(0)=1, р1(0)=0.
В результате, получаем следующие решения уравнений

Зависимости величин р0 и р1 от времени представлены на рисунке 41 - 44. В начальный момент времени (t=0) обучающийся заведомо находится в состоянии незнания (р0(0)=1, р1(0)=0). В процессе обучения с увеличением времени t вероятность р0 уменьшается и в пределе (при t®¥) равна  . Величина р1(t), дополняющая р0(t) до единицы, в процессе обучения возрастает.
. Величина р1(t), дополняющая р0(t) до единицы, в процессе обучения возрастает.
Показатель знания имеет вид:

Предельное значение показателя знания получается из (3.17) при t®¥:
