Привести пример по модусу DATISI III-ой фигуры и свести к соответствующему модусу I – ой фигуры.
№1
Предмет логики. Под предметом науки понимается не нечто материальное, а то на что направленно ее внимание. Логика обращена к мысли используемой человеком в своей жизнедеятельности, в том числе и в познании. Таким образом предметом логики являются: 1) мыслительные формы или формы мысли, их свойства взаимосвязи и законы (правила), которым мысли подчиняются.
Речь выраженная в устной и письменной форме.
Предметом изучения диалектической логики служат законы развития человеческого мышления и основанные на них методологические принципы (объективность, всесторонность рассмотрения предмета, принцип историзма, раздвоение единого на противоположные стороны, восхождение от абстрактного к конкретному и др.).
Диалектическая логика — это один из способов познания диалектики реальности.
Формальная логика, использующая математические методы изучения реальности, в начале XX в. получила название «логистика», означающее искусство вычисления. Теперь данный термин почти вышел из употребления, уступив место терминам «математическая логика» или «символическая логика».
Формальная логика изучает форму как нечто отдельное, обособленное от содержания.
Предметом изучения формальной логики служит форма мышления.
2. Какое общее правило категорического силлогизма нарушено в следующем примере:
Общие правила категорического силлогизма:
1) правила терминов:
В категорическом силлогизме должно быть три и только три термина.
Средний термин доложен быть распределен по крайней мере в одной из посылок.
Термин не распределенный в посылках не может быть распределен в заключении.
2) правила посылок:
Из двух отрицательных посылок нельзя сделать никакого заключения.
Если одна из посылок отрицательная, то заключение отрицательное.
Из двух частных посылок нельзя сделать никакого заключения.
Если одна из посылок частная, то заключение частное.
1. Фигура. Большая посылка обязательно общее суждение, а меньшая посылка – утвердительное.
2. Фигура. Большая посылка всегда общее суждение – одна из посылок отрицательная
3. Фигура. Меньшая посылка утвердительное суждение, заключение частное.
№2
1. Возникновение логики как науки.
Логика как наука возникла в конце V – начале IV веков в Древней Греции (Афины) и много столетий считалась критерием образованности. Основателем логики считают древнегреческого философа Аристотеля. Предшественниками Аристотеля в развитии логической науки в Древней Греции были Парменид, Зенон Элейский, Сократ и Платон. Аристотель же впервые систематизировал доступные знания о логике, обосновал формы и правила логического мышления. В его трудах «Органон» («Орудия познания») были сформулированы основные законы мышления, такие как закон тождества, противоречия и исключенного третьего. Он также разработал теорию понятия и суждения, исследовал дедуктивное и силлогистическое умозаключения.
После Аристотеля в Древней Греции логика также разрабатывалась представителями школы стоиков. Большой вклад в развитие этой науки внесли оратор Цицерон и древнеримский теоретик ораторского искусства Квинтилиан.
В начале XIX века Г.В.Ф. Гегель указал на ее ограниченность и недостаточность с точки зрения отражения процесса движения мысли. Он отметил, что такая логика отражает не движение содержания мысли, а форму мыслительного процесса. Для компенсации этого недостатка Гегель создал новую диалектическую логику, а существовавшую до нее назвал формальной.
2. Приведите пример по модусу CELARENT I–ой фигуры категорического силлогизма.
Все философы не есть социологи
Все логики есть философы
Все логики не есть социологи
№3
1. Логика и язык.
Формальная логика — это наука об общих структурах правильного мышления в его языковой форме, раскрывающая лежащие в его основе закономерности.
Структура мышления — это различные способы группировки мыслей в процессе мышления. В отличие от самого мышления и, тем более, его структуры мы видим их внешнюю речевую форму.
Невозможно сделать мышление устойчивым предметом исследования, если только оно не облекается в форму речи (устной или письменной). Очевидно, речь — это эмпирический материал, служащий истоком для формальной логики. Но речь и язык как внешняя структура мышления интересуют логику как средство для ее выражения.
Логическими формами называются различные соединения мыслей, рассматриваемые как структурные образования мышления.
Предметом изучения логики являются формы и законы правильного мышления.
Мышление есть функция человеческого мозга, которая неразрывно связана с языком.
Функции естественного языка многочисленны и многогранны.
Язык – средство повседневного общения людей, средство общения в практической и научной деятельности. Языку свойственны такие функции как:
· хранение информации
· средство выражения эмоций
· средство познания
Язык является знаковой информационной системой, продуктом духовной деятельности человека. Накопленная информация передается с помощью знаков языка - слов.
Речь может быть устной или письменной, звуковой или незвуковой, внешней или внутренней, выраженной с помощью естественного или искусственных языков, в основе которых лежит естественный язык, сформулированы положения всех наук.
На базе естественных наук возникли искусственные языки науки. К ним принадлежат языки математики, символической логики, химии, физики.
Понятия выражаются посредством отдельных слов или словосочетаний, суждения и умозаключения – с помощью простых или сложных предложений. Поэтому логический анализ рассуждений тесно связан с анализом языка.
2. Приведите пример CAMESTRES II-ой фигуры категорического силлогизма.
Все логики есть философы
Все философы не есть социологи
Все логики не есть социологи
№4
1. Логика и аргументация.
(до жирненького) Процесс понимания тесно связан с аргументацией, под которой подразумевают рационально-логический способ убеждения.
Аргументация предполагает диалог, в ходе которого происходит обмен мыслями между его участниками. Чтобы убедить другого человека, необходимо, прежде всего, точно уяснить смысл тех понятий и утверждений, которые используются для этого и которые называются доводами или аргументами. Слушатель или оппонент только тогда их поймет и согласится с ними, когда они будут точно определены и обоснованы.
С логической точки зрения аргумент – это термин умозаключения, обретающий свой смысл только в рамках определенной формы логического следования. Так же как действующий фактор может рассматриваться в качестве причины лишь тогда, когда известно произведенное им следствие, через которое он и демонстрирует себя как причина, так же и некоторое высказывание Р становится аргументом лишь в силу демонстрации его определенного места в рассуждении, лишь в силу демонстрации его определенной логической связи с провозглашенным логическим следствием.
Назвать какое- либо высказывание аргументом недостаточно для того, чтобы оно было таковым, необходимо продемонстрировать его конкретную логическую связь с соответствующим следствием.
2. Приведите пример по модусу BOCARDO III фигуры простого категорического силлогизма.
Некоторые книги не есть учебники
Некоторые книги есть энциклопедии
Некоторые энциклопедии не есть учебники
№5
1. Общая характеристика понятия.
Ближайшие синонимы к слову «понятие» - слово, мысль, имя, смысл, определение, знак, суть вещи, значение.
Понятие — это мысль, обозначенная словом или словосочетанием и отражающая предмет или явление.
Во всех понятиях имеются три аспекта:
· языковой
· логический (мысленный)
· предметный
Понятие обозначает предмет и выражается словом.
Понятие — это не имя и не предмет, а то что является мысленным опосредующим звеном между предметом и именем, соотнося здесь и теперь данный предмет с данным именем.
Понятие — это форма мысли, отображающая единство общих и отличительных признаков предметов и явлений.
Понять значит постичь значение слова или словосочетания, а поскольку в словах обобщена мысль о предметах или явлениях, то понятие выражает единство, объединяющее множество предметов или явлений. В понятии можно выделить количественную сторону — объем и качественную — содержание.
понятие

|
слово предмет
Привести пример по модусу DATISI III-ой фигуры и свести к соответствующему модусу I – ой фигуры.
Все планеты Солнечной Системы вращаются вокруг Солнца.
Некоторые планеты Солнечной Системы имеют атмосферу.
Некоторые имеющие атмосферу планеты, являются вращающимися вокруг Солнца.
M a P
M i S Datisi
S i P
Действия:
1) Обращение S
Все планеты Солнечной Системы вращаются вокруг Солнца.
Некоторые имеющие атмосферу планеты - планеты Солнечной Системы.
Некоторые вращающиеся вокруг Солнца планеты имеют атмосферу.
M a P
S i M Darii
S i P
№6
1. Содержание и объем понятия
Объём понятия (в логике) — совокупность предметов, охватываемых понятием. Объём и содержание понятия выступают как основные характеристики понятия, подчиняясь при этом закону обратного отношения между содержанием и объёмом понятия (увеличение объёма приводит, как правило, к уменьшению содержания и наоборот). Изменение понятия обычно предполагает изменение его объёма.
Части, входящие в объём понятия, называют классами или множествами. Они, в свою очередь, включают в себя более мелкие части (подклассы или подмножества). Отдельный предмет, принадлежащий к классу, называется элементом класса.
Соотношения между объёмами различных понятий можно иллюстрировать графически с помощью кругов Эйлера.
Содержание понятия — это совокупность существенных и отличительных признаков предмета, качества или множества однородных предметов, отражённых в этом понятии, поскольку с точки зрения логики всякое понятие имеет содержание и объём. Например, содержанием понятия «коррупция» является совокупность двух существенных признаков: «сращение государственных структур со структурой преступного мира» и «подкуп и продажность общественных и политических деятелей, государственных чиновников и должностных лиц».
О содержании понятия нельзя говорить в отрыве от его объёма. Объёмом понятия называется множество обобщённых в нём предметов. Например, под объёмом понятия «товар» подразумевается множество всех изделий, предлагаемых рынку как сейчас, так и в прошлом или в будущем.
Закон обратного отношения между объемом и содержанием понятия
Объём понятия может входить в объём другого понятия и составлять при этом лишь его часть. Например, объём понятия «фирменный знак» целиком входит в объём другого, более широкого понятия «знак». При этом содержание первого понятия оказывается шире, потому что содержит больше отличительных признаков, чем содержание второго.
Исходя из этого имеется следующий закон: чем шире объём, тем проще его содержание, и наоборот.
2. Привести пример по модусу BOCARDO III-ой фигуры и свести к соответствующему модусу I – ой фигуры.
Некоторые музыканты не композиторы.
Все музыканты обладают хорошим слухом.
Некоторые люди, обладающие хорошим слухом, не являются композиторами.
M o P
M a S Bocardo
S o P
Действия:
1) Приведение от противного (приведение к абсурду (Bocardo и Baroco))
Допустим, что:
Все люди с хорошим слухом — композиторы.
Все музыканты обладают хорошим слухом.
Значит, все музыканты композиторы.
M a P
S a M Barbara
S a P
Заключение «Значит, все музыканты композиторы.» противоречит исходному «Некоторые люди, обладающие хорошим слухом, не являются композиторами.», следовательно заключение Bocardo верно.
№7
1. Виды понятий
1) по объему:
единичные (отображающие множество, состоящее из одного элемента; я, ты, этот человек)
общие (отображающее множество, состоящее из двух и более элементов; человек, звезда)
нулевые (отображающие множество не содержащее ни одного элемента)
2) по содержанию:
конкретные (отражают сами предметы; человек, город, линия, решение суда)
абстрактные (отображают свойства и отношения между предметами; человечность, перенаселенность города, небесная линия Петербурга, справедливость)
3) также понятия делятся на:
собирательные (признаки которых относятся не к каждому элементу множества, а ко всему множеству в целом; в понятии «толпа» признак быть толпой относится к некоторому целому, а не к отдельным людям, составляющим эту толпу)
разделительные (признаки которых относятся к каждому элементу множества предметов; дом, театр, справедливость, число)
2. Определите вид силлогизма:
Виды умозаключений (силлогизмов):
1) По характеру направленности процесса:
дедуктивные (от общего к частному)
индуктивные (от частного к общему. Не достоверный, а вероятный вывод)
традуктивные (по аналогии - переход к суждению той же степени частности)
2) По опосредованности:
непосредственные
· умозаключения по логическому квадрату
· превращение
· обращение
· противопоставление предикату
опосредованные.
№8
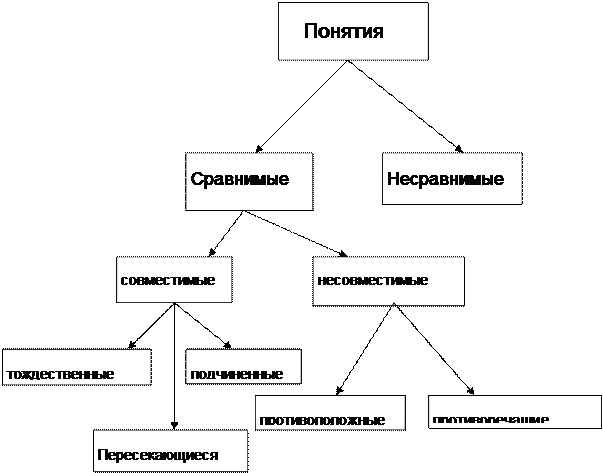
1. Отношения между понятиями по объему
Понятия по объему делятся на:
· сравнимые (имеют общие элементы в объемах и/или содержаниях, имеют общий признак: «студент» и школьник – да, студент и треугольник – нет):
совместимые (имеют общие элементы в объемах)
тождественные (тождество — объемы понятий полностью совпадают; столица, административный центр страны)
подчиненные (подчинение — объем одного понятия полностью входит в объем другого, но не исчерпывает его, а составляет лишь часть; музей, краеведческий музей)
пересеченные (пересечение — объемы понятий совпадают частично, таким образом, объем одного понятия частично входит в объем другого и наоборот; студент, музыкант)
несовместимые (нет общих элементов в объемах, но есть общие элементы в содержании;)
соподчинение (два несовместимых понятия по отношению к общему для них роду)
противоречие (два несовместимых понятия, исчерпывающих объем общего для них родового понятия; живое, неживое; розовое, не розовое)
противоположность (понятия, в которых мыслятся крайние моменты в последовательном ряду явлений; человек, лошадь; добрый, злой)
· несравнимые (не имеют общего родового понятия)
2. Определите модус условно-категорического силлогизма:
Модусы условно-категорических силлогизмов:
| Конструктивный условно-категорический силлогизм. Модус — Ponens. | Деструктивный условно-категорический силлогизм. Модус — Tollens. |
| Если А, то В А Значит, В | Если А, то В не-В Значит, не-А |
№9
1. Операции с понятиями.
1. Операция обобщения:
Обобщение — логическая операция, при которой переходят от видового понятия к родовому понятию (то есть расширяют множество мыслимых предметов путем изъятия видовых признаков)
Процесс обобщения представляет собой иерархию подчиненных друг другу понятий, что в круговых схемах изображается концентрическими кругами с центробежным ростом объема понятий.
(автор «Евгения Онегина» – гениальный человек – человек)
2. Операция ограничения:
Ограничение — логическая операция, при которой переходят от родового понятия к видовому понятию (то есть сужают количество мыслимых предметов, прибавляя видовой признак)
Процесс ограничения является процессом обратным обобщению с центростремительным уменьшением объемов понятий. И тот и другой процессы имеют пределы.
Закон обратного отношения между объемом и содержанием понятий:
Увеличение объема приводит к уменьшению содержания и наоборот.
То есть обобщая, мы увеличиваем объем понятий с одновременным уменьшением числа признаков, то есть содержания; ограничивая, мы уменьшаем объем понятий с одновременным добавлением признаков, то есть увеличиваем содержание.
(человек- умный человек- очень умный человек- великий античный философ)
3. Операция логического деления:
Деление — логическая операция раскрывающая объем родового понятия путем перечисления его видов.
· Дихотомическое деление (наиболее простое) — выделение в родовом понятии видового понятия, противоречащего видовому.
· Деление по видообразующему признаку (более сложное) — деление по видоизменению признака. В нем различают:
делимое — родовое понятие
основание деления — видообразующий признак
члены деления — видовые пониятия.
Правила деления:
1) Деление должно производиться по одному основанию.
2) Деление должно быть соразмеренным, то есть объем делимого понятия должен быть равен сумме объемов членов деления.
3) Деление должно быть последовательным, без скачков.
4) Члены деления должны исключать друг друга, то есть быть в отношении несовместимости.
Ошибки логического деления:
· Деление по разным основаниям
· Неполное деление
· Пересечение видов (Виды никогда не пересекаются!)
(понятие «животное», делимое по основанию «среда обитания»: животное, обитающее в воде; животное обитающее на (в) земле, животное, обитающее в воздухе)
4. Логическая операция определения:
Определение (дефиниция) — логическая операция, раскрывающая содержание путем перечисления его родового и видовых признаков. Такое определение через род и вид называют классическим, или аристотелевским.
Структура определения:
· Определяемое понятие (Dfd) – понятие, содержание которого требуется раскрыть.
· Определяющее понятие (Dfn) – понятие, раскрывающее содержание определяемого понятия. В нем выделяют родовой и видовые признаки.
Правила определения:
1) Определение должно быть соразмеренным, то есть объем определяемого понятия должен быть равен объему определяющего понятия: Dfd = Dfn.
2) Определение не должно содержать круга, то есть определяющее понятие не должно раскрываться через определяемое понятие.
3) Определение должно быть ясным, однозначным, не содержать метафор и сравнений.
4) Определение по возможности не должно быть отрицательным.
Ошибки в определении:
· Слишком широкое определение: Dfd < Dfn.
· Слишком узкое определение: Dfd > Dfn.
· Круг в определении
(человек – животное, обладающее разумом)
5. Классификация:
Классификация — это распределение предметов некоторого целого в иерархической (соподчиненной) структуре понятий.
Основы классификации у Аристотеля - «Древо Порфирия»:
«Древо Порфирия» - иерархия сущностей (образ дерева был выбран так как в нем отражена идея жизни, развития):
· Высший род
· Промежуточные роды
· Ближайший род
· Конечные (неделимые) виды
Так же классификацию иерархию можно наглядно представить: концентрическими кругами, делением плоскости, делением отрезков.
С логической точки зрения классификацией является родо-видовое деление, а не деление целого на части. Первое отношение транзитивно, а второе — нет, а аристотилевское учение о сущности построено на отношении транзитивности.
Классификация представляет собой полное деление какой-либо области по нескольким основаниям.
6. Каталогизация:
Каталогизация — перечисление, то есть анализ и деление целого на части так, что группы образуются не на основе существенного, а на основе привходящего признака.
2. Определите модус разделительно-категорического силлогизма:
Модусы разделительно-категорических силлогизмов:
| Утверждающе-отрицающий разделительно-категорический силлогизм. Модус — Ponendo-Tollens. | Отрицающе-утверждающий разделительно-категорический силлогизм. Модус — Tollendo-Ponens. |
| А либо В А Значит, не-В | А либо В Не-В Значит, А |
№10
1. Общая характеристика суждения.
Ближайший синоним к слову «суждение» - высказывание, но также существуют и другие синонимы: предположение, пропозиция, утверждение, тезис, речь, сентенция, положение, теорема, лемма.
Суждение — это форма мысли, в которой утверждается, либо отрицается наличие признака у предмета, и которая обладает одним из двух логических значений: истина или ложь.
Все суждения выражаются в форме повествовательных предложений.
Суждения делятся на:
1) простые
2) сложные (суждения, образованные из простых при помощи логических союзов)
Строение простого суждения:
· Субъект суждения (S) — это подлежащий рассмотрению предмет мысли (логическое подлежащее)
· Предикат (Р) — то, что рассказывается о предмете мысли (логическое сказуемое)
· Связка — выражает отношение между субъектом и предикатом (то есть между предметом и его свойством)
Схема строения простого суждения: S связка Р
Деление простых суждений:
1) по качеству:
утвердительные (связка предписывает предикат субъекту)
отрицательные (связка отделяет предикат от субъекта)
2) по количеству:
общие (предикат предписывается (или не предписывается) всем предметам класса)
частные (предикат предписывается (или не предписывается) части предметов класса)
единичные (предикат предписывается (или не предписывается) одному элементу класса)
3) объединенная классификация (по количеству и качеству):
А — общеутвердительные суждения: Все S есть Р
I — частноутвердительные суждения: Некоторые S есть Р
Е — общеотрицательные суждения: Все S не есть Р
О — частноотрицательные суждения: Некоторые S не есть Р.
Распределенность терминов в простом суждении:
Термин суждения (субъект, предикат) считается распределенным, если в данном суждении он мыслится во всем объеме.
Правила распределенности:
· Субъект всегда распределен в общих и единичных суждениях.
· Предикат всегда распределен в отрицательных суждениях.
2. Определите, к какому виду дилеммы относится данный пример - к конструктивной или деструктивной:
Виды условно-разделительных силлогизмов (дилемм):
| Простая конструктивная дилемма | Простая деструктивная дилемма | Сложная конструктивная дилемма | Сложная деструктивная дилемма |
| Если А, то В, если С то В А или С В | Если А, то В, если A то C Не-В или не-C Не-А | Если А, то В, если С то D А или С В или D | Если А, то В, если С то D Не-В или не-D Не-А или не-С |
№11
1. Отношения между суждениями в логическом квадрате.
ЛОГИЧЕСКИЙ КВАДРАТ
схема, выражающая отношения с т. зр. истинности и ложности между общеутвердительным,общеотрицательным, частноутвердительным и частноотрицательным суждениями традиц. логики,имеющими один и тот же субъект и один и тот же предикат и обозначаемыми соответственно буквами А, Е, I,О; предложен в 11 в. Михаилом Пселлом.
Отношение п о д ч и н е н и я характеризуется тем, что истинность подчиняющего суждения (А или Е)обусловливает истинность соответствующего подчиненного суждения (I или О), а ложность подчиненногосуждения обусловливает ложность подчиняющего суждения; отношение п о д п р о т и в н о с т и(субконтрарности) характеризуется тем, что ложность одного из подпротивных суждений обусловливаетистинность другого.
(Об отношениях противности и противоречия см. Контрарное отношение и Контрадикторное отношение).

2. Какая ошибка имеет место в следующем примере определения понятия:
Правила определения:
5) Определение должно быть соразмеренным, то есть объем определяемого понятия должен быть равен объему определяющего понятия: Dfd = Dfn.
6) Определение не должно содержать круга, то есть определяющее понятие не должно раскрываться через определяемое понятие.
7) Определение должно быть ясным, однозначным, не содержать метафор и сравнений.
8) Определение по возможности не должно быть отрицательным.
Ошибки в определении:
· Слишком широкое определение: Dfd < Dfn.
· Слишком узкое определение: Dfd > Dfn.
· Круг в определении
№12
1. Сложные суждения. Таблицы истинности для логических союзов.
Суждения делятся на:
1) простые
2) сложные (суждения, образованные из простых при помощи логических союзов).(кролик есть млекопитающее отряда лагоморфа, а заяц есть млекопитающее отряда лепус)
Строение простого суждения:
· Субъект суждения (S) — это подлежащий рассмотрению предмет мысли (логическое подлежащее)
· Предикат (Р) — то, что рассказывается о предмете мысли (логическое сказуемое)
· Связка — выражает отношение между субъектом и предикатом (то есть между предметом и его свойством)
Схема строения простого суждения: S связка Р
Схема строения сложного суждения: S есть Р
S есть Р1 и S есть Р2
S1 есть Р и S2 есть Р
Таблица логических союзов:
| Логический союз | Символ | Аналог в естественном языке |
| 1. Конъюкция | & | «и», «а», «но», «тогда как», «при том, что», «,» и т.п. |
| 2. Слабая дизъюнкция | v | «или», «или..., или...» |
| 3. Строгая дизъюнкция | «либо», «либо..., либо...» | |
| 4. Импликация | «если..., то...» | |
| 5. Эквиваленция | «тогда и только тогда, когда» | |
| 6. Отрицание | ~ | «наверно, что», «ложно, что» |
Таблицы истинности для логический союзов:
1. Конъюкция — соединительный союз: «он сдал все экзамены, но еще не защитил диплом»;
| В | С | В & С |
| Истинно | Истинно | Истинно |
| Ложно | Истинно | Ложно |
| Истинно | Ложно | Ложно |
| Ложно | Ложно | Ложно |
Конъюкция В & С истина тогда и только тогда, когда оба конъюнкта истинны, и ложна, когда хотя бы один из конъюнктов ложен.
2. Слабая дизъюнкция: B и/или C: «Я полечу на Юг на самолете или поеду на поезде»; «Я куплю новую квартиру или перееду жить к своей сестре».
| В | С | В v С |
| Истинно | Истинно | Истинно |
| Ложно | Истинно | Истинно |
| Истинно | Ложно | Истинно |
| Ложно | Ложно | Ложно |
Слабая дизъюнкция В v С ложна тогда и только тогда, когда оба дизъюнкта ложны, и истинна, когда хотя бы один из дизъюнктов истинен.
3. Строгая дизъюнкция — строгое разделение: либо B, либо С: либо Н. преступник, либо М. - преступник, но не оба вместе
| В | С | В С |
| Истинно | Истинно | Ложно |
| Ложно | Истинно | Истинно |
| Истинно | Ложно | Истинно |
| Ложно | Ложно | Ложно |
Строгая дизъюнкция В С истина тогда и только тогда, когда В и С имеют разные логические значения, и ложна, когда В и С имеют одинаковые логические значения.
4. Импликация — условный союз: если В, то С: «Если будет хорошая погода, мы пойдем в лес»;
| В | С | В С |
| Истинно | Истинно | Истинно |
| Ложно | Истинно | Истинно |
| Истинно | Ложно | Ложно |
| Ложно | Ложно | Истинно |
Импликация В С ложна только в одном случае, если основание И истинно, а следствие С — ложно, и истинна во всех остальных случаях.
5. Эквиваленция — союз эквивалентности: В тогда и только тогда, когда С:
| В | С | В С |
| Истинно | Истинно | Истинно |
| Ложно | Истинно | Ложно |
| Истинно | Ложно | Ложно |
| Ложно | Ложно | Истинно |
Эквивалентное суждение В С истинно тогда и только тогда, когда оба простых суждения В и С имеют одинаковые логические значения, и ложно, когда В и С имеют различные логические значения.
2. Какая ошибка имеет место в следующем примере деления:
Правила деления:
5) Деление должно производиться по одному основанию.
6) Деление должно быть соразмеренным, то есть объем делимого понятия должен быть равен сумме объемов членов деления.
7) Деление должно быть последовательным, без скачков.
8) Члены деления должны исключать друг друга, то есть быть в отношении несовместимости.
Ошибки логического деления:
· Деление по разным основаниям
· Неполное деление
· Пересечение видов (Виды никогда не пересекаются!)
№13, 14
1. Полная и неполная индукция, популярная и научная индукция.
Индукция — это умозаключение от частного к общему. В результате такого умозаключения получается не достоверный, а вероятностный вывод.
Индуктивные умозаключения (кроме полной индукции) относятся к вероятностным и представляют собой переход от частных и единичных суждений к общим:
полная индукция
Схема полной индукции:
S1 есть P
S2 есть P
…
Sn есть P
S1 … Sn – исчерпывают все предметы класса S
Следовательно, все S есть P
Например, когда преподаватель, сделав перекличку своих учеников, убеждается, что каждый из учеников данного класса присутствует на уроке, то он может сделать заключение «Все ученики данного класса явились на урок». Его рассуждение осуществляете» по принципу полной индукции.
Другой пример: установление того, что каждый из документов, необходимых для оценки готовности уголовного дела для передачи в суд, имеется, позволяет с полным основанием сделать заключение, что «Все документы имеются» и дело следует передать в суд.
неполная индукция — это когда заключение о принадлежности этого признака некоторой части предметов класса
Схема неполной индукции:
S1 есть P
S2 есть P
…
Sn есть P
S1 … Sn – часть класса S
Вероятно, все S есть P
Виды неполной индукции:
1) Простая перечислительная (или популярная)
Вывод по такой индукции делается при неполном знании об имеющихся фактах и случайном характере их отбора. «Береги платье снову, а честь смолоду», «Старый друг лучше новых двух» и т. д.
Например, почти во всех учебниках логики приводится пример с выводом, полученным с помощью неполной индукции, - «Все лебеди белые», который оказался ложным после того, когда в Австралии были обнаружены черные лебеди.
2) Научная индукция
В ней используются методы, повышающие достоверность вывода, прежде всего, методы установления причинной связи явлений — методы Бэкона-Милля:
1. Метод сходства
2. Метод различия
3. Соединенный метод сходства и различия
4. Метод сопутствующих изменений
5. Метод остатков
2(13). Обобщить, а затем ограничить следующие понятия:
1. Операция обобщения:
Обобщение — логическая операция, при которой переходят от видового понятия к родовому понятию (то есть расширяют множество мыслимых предметов путем изъятия видовых признаков)
Процесс обобщения представляет собой иерархию подчиненных друг другу понятий, что в круговых схемах изображается концентрическими кругами с центробежным ростом объема понятий.
2. Операция ограничения:
Ограничение — логическая операция, при которой переходят от родового понятия к видовому понятию (то есть сужают количество мыслимых предметов, прибавляя видовой признак)
Процесс ограничения является процессом обратным обобщению с центростремительным уменьшением объемов понятий. И тот и другой процессы имеют пределы.
Закон обратного отношения между объемом и содержанием понятий:
Увеличение объема приводит к уменьшению содержания и наоборот.
То есть обобщая, мы увеличиваем объем понятий с одновременным уменьшением числа признаков, то есть содержания; ограничивая, мы уменьшаем объем понятий с одновременным добавлением признаков, то есть увеличиваем содержание.
2(14). Проведите структурный анализ следующих простых суждений:
Строение простого суждения:
· Субъект суждения (S) — это подлежащий рассмотрению предмет мысли (логическое подлежащее)
· Предикат (Р) — то, что рассказывается о предмете мысли (логическое сказуемое)
· Связка — выражает отношение между субъектом и предикатом (то есть между предметом и его свойством)
Схема строения простого суждения: S связка Р
Распределенность терминов в простом суждении:
Термин суждения (субъект, предикат) считается распределенным, естли в данном суждении он мыслится во всем объеме.
Правила распределенности:
· Субъект всегда распределен в общих и единичных суждениях.
· Предикат всегда распределен в отрицательных суждениях.
| Общеутвердительные суждения (A) | Частноутвердительные суждения (I) | Общеотрицательные суждения (E) | Частноотрицательные суждения (O) | ||
  S+aP- S+aP-
| S+aP+ | S-iP- | S-iP+ | S+eP+ | S-oP+ |
№15
1. Метод сходства.
Индуктивные методы установления причинной связи явлений (методы Бэкона-Милля):
1. Метод сходства
2. Метод различия
3. Соединенный метод сходства и различия
4. Метод сопутствующих изменений
5. Метод остатков
Метод сходства:
Если два или более случаев наблюдаемого явления сходны только в одном обстоятельстве, то это одно обстоятельство, вероятно, и есть причина данного явления.
Схема метода сходства:
При условиях ABC возникает явление a
При условиях ADE возникает явление a
При условиях AFG возникает явление a
Вероятно, обстоятельство A является причиной явления a.
Ошибки в индуктивных умозаключениях:
1) «поспешное обобщение»
2) «после этого, значит, по причине этого».
2. Определить количество и качество суждения, его буквенное обозначение:
Строение простого суждения:
· Субъект суждения (S) — это подлежащий рассмотрению предмет мысли (логическое подлежащее)
· Предикат (Р) — то, что рассказывается о предмете мысли (логическое сказуемое)
· Связка — выражает отношение между субъектом и предикатом (то есть между предметом и его свойством)
Схема строения простого суждения: S связка Р
Деление простых суждений:
1) по качеству:
утвердительные (связка предписывает предикат субъекту)
отрицательные (связка отделяет предикат от субъекта)
2) по количеству:
общие (предикат предписывается (или не предписывается) всем предметам класса)
частные (предикат предписывается (или не предписывается) части предметов класса)
единичные (предикат предписывается (или не предписывается) одному элементу класса)
3) объединенная классификация (по количеству и качеству):
А — общеутвердительные суждения: Все S есть Р
I — частноутвердительные суждения: Некоторые S есть Р
Е — общеотрицательные суждения: Все S не есть Р
О — частноотрицательные суждения: Некоторые S не есть Р.
№16
1. Метод различия.
Метод различия:
Если случаи, в котором явление наступает, и случии, в котором данное явление не наступает, отличаются только одним обстоятельством, то это обстоятельство, вероятно, есть причина данного явления.
Схема метода различия:
При условиях ABCD явление a возникает.
При условиях BCD явление a не возникает.
Вероятно, обстоятельство A является причиной явления a.
Ошибки в индуктивных умозаключениях:
3) «поспешное обобщение»
4) «после этого, значит, по причине этого».
2. Составьте суждение из следующей пары понятий, учитывая распределенность их объемов:
Схема строения простого суждения: S связка Р
Распределенность терминов в простом суждении:
Термин суждения (субъект, предикат) считается распределенным, естли в данном суждении он мыслится во всем объеме.
Правила распределенности:
· Субъект всегда распределен в общих и единичных суждениях.
· Предикат всегда распределен в отрицательных суждениях.
№17
1. Соединенный метод сходства и различия.
Соединенный метод сходства и различия:
Данный метод значительно усиливает степень вероятности вывода благодаря тому, что рассматривает два ряда случаев. Первый ряд соответствует методу сходства, а второй вариант соответствует методу различия:
1) Метод сходства:
Если два или более случаев наблюдаемого явления сходны только в одном обстоятельстве, то это одно обстоятельство, вероятно, и есть причина данного явления.
Схема метода сходства:
При условиях ABC возникает явление a
При условиях ADE возникает явление a
При условиях AFG возникает явление a
Вероятно, обстоятельство A является причиной явления a
2) Метод различия:
Если случаи, в котором явление наступает, и случии, в котором данное явление не наступает, отличаются только одним обстоятельством, то это обстоятельство, вероятно, есть причина данного явления.
Схема метода сходства:
При условиях ABCD явление a возникает.
При условиях BCD явление a не возникает.
Вероятно, обстоятельство A является причиной явления a
Схема соединенного метода сходства и различия:
При условиях ABC возникает явление a
При условиях ADE возникает явление a
При условиях ABCD явление a возникает.
При условиях BCD явление a не возникает.
Вероятно, обстоятельство A является причиной явления a.
2. Определите вид сложного суждения и изобразите таблицу истинности используемого в нем логического союза:
Деление простых суждений:
Объединенная классификация (по количеству и качеству):
А — общеутвердительные суждения: Все S есть Р
I — частноутвердительные суждения: Некоторые S есть Р
Е — общеотрицательные суждения: Все S не есть Р
О — частноотрицательные суждения: Некоторые S не есть Р.
Таблицы истинности для логический союзов:
1. Конъюкция — соединительный союз:
| В | С | В & С |
| Истинно | Истинно | Истинно |
| Ложно | Истинно | Ложно |
| Истинно | Ложно | Ложно |
| Ложно | Ложно | Ложно |
Конъюкция В & С истина тогда и только тогда, когда оба конъюнкта истинны, и ложна, когда хотя бы один из конъюнктов ложен.
2. Слабая дизъюнкция: B и/или C:
| В | С | В v С |
| Истинно | Истинно | Истинно |
| Ложно | Истинно | Истинно |
| Истинно | Ложно | Истинно |
| Ложно | Ложно | Ложно |
Слабая дизъюнкция В v С ложна тогда и только тогда, когда оба дизъюнкта ложны, и истинна, когда хотя бы один из дизъюнктов истинен.
3. Строгая дизъюнкция — строгое разделение: либо B, либо С:
| В | С | В С |
| Истинно | Истинно | Ложно |
| Ложно | Истинно | Истинно |
| Истинно | Ложно | Истинно |
| Ложно | Ложно | Ложно |
Строгая дизъюнкция В С истина тогда и только тогда, когда В и С имеют разные логические значения, и ложна, когда В и С имеют одинаковые логические значения.
4. Импликация — условный союз: если В, то С:
| В | С | В С |
| Истинно | Истинно | Истинно |
| Ложно | Истинно | Истинно |
| Истинно | Ложно | Ложно |
| Ложно | Ложно | Истинно |
Импликация В С ложна только в одном случае, если основание И истинно, а следствие С — ложно, и истинна во всех остальных случаях.
5. Эквиваленция — союз эквивалентности: В тогда и только тогда, когда С:
| В | С | В С |
| Истинно | Истинно | Истинно |
| Ложно | Истинно | Ложно |
| Истинно | Ложно | Ложно |
| Ложно | Ложно | Истинно |
Эквивалентное суждение В С истинно тогда и только тогда, когда оба простых суждения В и С имеют одинаковые логические значения, и ложно, когда В и С имеют различные логические значения.
№18
1. Метод остатков.
Умозаключение — это прием рассуждения, посредством которого из некоторого исходного знания можно получить новое, выводное знание. Вывод импликантен (скрыт) в суждении.
Умозаключение — это всегда процесс. Процесс движения от одной мысли к другой.
Индуктивные методы установления причинной связи явлений (методы Бэкона-Милля):
1. Метод сходства
2. Метод различия
3. Соединенный метод сходства и различия
4. Метод сопутствующих изменений
5. Метод остатков
Метод остатков:
Если известно, что причиной исследуемого явления не служат необходимые для него обстоятельства, кроме одного, то это обстоятельство, вероятно, и есть причина данного явления.
Схема метода остатков:
Обстоятельство ABC вызывает явление abc
Обстоятельство B вызывает явление b
Обстоятельство C вызывает явление c
Вероятно, обстоятельство A есть причина явления a.
2. Обратите следующие суждения:
Операция обращения:
Обращение — логическая операция, при которой субъект и предикат меняются местами без изменения качества суждения. Различают:
· чистое (или простое) обращение, при котором не только качество, но и количество суждения не меняется.
· обращение с ограничением, при котором изменяется количество обращенного суждения.
№19
1. Метод сопутствующих изменений.
Умозаключение — это прием рассуждения, посредством которого из некоторого исходного знания можно получить новое, выводное знание. Вывод импликантен (скрыт) в суждении.
Умозаключение — это всегда процесс. Процесс движения от одной мысли к другой.
Индуктивные методы установления причинной связи явлений (методы Бэкона-Милля):
1. Метод сходства
2. Метод различия
3. Соединенный метод сходства и различия
4. Метод сопутствующих изменений
5. Метод остатков
Метод сопутствующих изменений:
Если какое-либо явление изменяется определенным образом всякий раз, когда изменяется предшествующее ему явление, то эти явления, вероятно, находятся в причинной связи друг с другом.
Схема метода сопутствующих изменений:
При условиях A*BC возникает явление a*.
При условиях A**BC возникает явление a**.
При условиях A***BC возникает явление a***.
Вероятно, обстоятельство A есть причина явления a.
2. Следуя отношениям суждений в логическом квадрате, вывести опосредованным путем из ложности суждения вида I ложность суждения вида А.
I ложно ð A ложно, так как:

 1) I ложно ð O истинно ð A ложно: А E
1) I ложно ð O истинно ð A ложно: А E
 I O
I O


 2) I ложно ð E истинно ð A ложно: А E
2) I ложно ð E истинно ð A ложно: А E
I O



 3) I ложно ð E истинно ð O истинно ð A ложно: А E
3) I ложно ð E истинно ð O истинно ð A ложно: А E
I O
№20
1. Закон тождества
Законы формальной логики — это схемы всегда истинных высказываний.
Формальная логика — это наука об общих структурах правильного мышления в его языковой форме, раскрывающая лежащие в его основе закономерности.
Формулы законов логики называются тождественно-истинными формулами, ибо они принимают значение «истина» независимо от того, какие значения принимают входящие в их состав элементарные формулы: Р или не-Р
Основные законы логики:
1. Закон тождества
2. Закон противоречия (Закон непротиворечия)
3. Закон исключения третьего
4. Закон достаточного основания
Закон тождества:
В процессе рассуждения мысль должна сохранять свое основное содержание:
Если Р истинно, то Ристинно
Р ð Р
Несоблюдение закона тождества выражается в двусмысленности понятий, их подмене и т.д.
2. Превратить следующие суждения:
Операция превращения:
Превращение — логическая операция, посредством которой меняют качество суждения путем установления совместимости субъекта (S) с понятием, противоречащим предикату (не-Р):
S есть Р S не есть Р
S не есть не-Р S есть не-Р
№21
1. Аксиоматический метод в науке.
Аксиоматический метод – метод построения теорий, в соответствии с которым разрешается пользоваться в доказательствах лишь аксиомами и ранее выведенными из них утверждениями.
Основания для применения аксиоматического метода могут быть разными, что обычно приводит к различению аксиом не только по их формулировкам, но и по их методологическим (прагматическим) статусам. Например, аксиома может иметь статус утверждения, или статус предположения, или статус лингвистического соглашения о желаемом употреблении терминов. Иногда это различие в статусах отражается в названиях аксиом .
Учет статусов аксиом обязателен, так как можно, например, изменить содержание аксиоматической теории, не изменив при этом ни формулировку, ни семантику аксиом, а поменяв лишь их статус, объявив, скажем, одну из них новым постулатом значения.
Аксиоматический метод был впервые продемонстрирован Евклидом в его «Началах», хотя понятия аксиомы, постулата и определения рассматривались уже Аристотелем. В частности, к нему восходит толкование аксиом как необходимых общих начал доказательства. Понимание аксиом как истин самоочевидных сложилось позднее, став основным с появлением школьной логики Пор-Рояля, для авторов которой очевидность означает особую способность души осознавать некоторые истины непосредственно (в чистом созерцании, или интуиции). Убеждение Канта в априорном синтетическом характере геометрии Евклида зависит от этой традиции не считать аксиомы лингвистическими соглашениями или предположениями. Открытие неевклидовой геометрии (Гаусс, Лобачевский, Бойяи); появление в абстрактной алгебре новых числовых систем, причем сразу целых их семейств; появление переменных структур вроде групп; наконец, обсуждение вопросов типа «какая геометрия истинна?» – все это способствовало осознанию двух новых, по сравнению с античным, статусов аксиом:
· аксиом как описаний (классов возможных универсумов рассуждений)
· аксиом как предположений, а не самоочевидных утверждений.
Так сформировались основы современного понимания аксиоматического метода. Это развитие аксиоматического метода становится особенно наглядным при сопоставлении «Начал» Евклида с «Основаниями геометрии» Д.Гильберта – новой аксиоматики геометрии, базирующейся на высших достижениях математики XIX века.
К концу того же века Дж.Пеано дал аксиоматику натуральных чисел. Далее аксиоматический метод был использован для спасения теории множеств после нахождения парадоксов. При этом аксиоматический метод был обобщен и на логику. Гильберт сформулировал аксиомы и правила вывода классической логики высказываний, а П.Бернайс – логики предикатов.
Ныне аксиоматическое задание является стандартным способом определения новых логик и новых алгебраических понятий. Сейчас аксиоматические теории нередко формулируются как формализованные системы, содержащие точное описание логических средств вывода теорем из аксиом. Доказательство в такой теории представляет собой последовательность формул, каждая из которых либо является аксиомой, либо получается из предыдущих формул последовательности по одному из принятых правил вывода. К аксиоматической формальной системе предъявляются требования непротиворечивости, полноты, независимости системы аксиом и т. д.
Аксиоматический метод является лишь одним из методов построения научного знания. Он имеет ограниченное применение, поскольку требует высокого уровня развития аксиоматизируемой содержательной теории. Как показал известный математик и логик К. Гёдель, достаточно богатые научные теории не допускают полной аксиоматизации. Это свидетельствует об ограниченности аксиоматического метода и невозможности полной формализации научного знания. Поэтому в последние десятилетия по мере развития моделей теории аксиоматический метод стал в почти обязательном порядке дополняться теоретико-модельным.
2. Соблюдается ли закон непротиворечия в следующем рассуждении:
Закон непротиворечия (Закон противоречия):
Два противоположных суждения не могут быть истинными в одно и то же время и в одном и том же отношении: Неверно, что Р и не-Р
№22
1. Общая характеристика умозаключения.
Ближайший синоним к слову «умозаключение» - высказывание, но также существуют и другие синонимы: речь, рассуждение, размышление, следование, расследование, вывод, выведение, последовательность..
Умозаключение — это прием рассуждения, посредством которого из некоторого исходного знания можно получить новое, выводное знание. Вывод импликантен (скрыт) в суждении.
Умозаключение — это всегда процесс. Процесс движения от одной мысли к другой.
Строение умозаключения:
· посылки (исходное значение которых дано и требуется доказать)
· заключение (вывод)
· правило следования
Правило следования:
M a P
S a M , где а — общеутвердительное суждение
S a P
Виды умозаключений (силлогизмов):
1) По характеру направленности процесса:
дедуктивные (от общего к частному)
индуктивные (от частного к общему. Не достоверный, а вероятностный вывод):
· полная индукция
· неполная индукция:
простая перечислительная (или популярная)
научная
традуктивные (по аналогии - переход к суждению той же степени частности):
· нестрогая аналогия
· структурная аналогия
2) По опосредованности:
непосредственные
· умозаключения по логическому квадрату
· превращение
· обращение
· противопоставление предикату
опосредованные.
2. Соблюдается ли закон исключенного третьего в следующем рассуждении:
Закон исключения третьего:
Из двух противоречащих друг другу суждений одно — истинно, другое — ложно, а третьего суждения не дано: Либо Р, либо не-Р.
№23
1. Общая характеристика доказательства.
Доказательство — логическая процедура установления истинности какого-либо суждения при помощи других суждений, истинность которых уже установлена.
Состав доказательства:
· Тезис — суждение, истинность которого следует доказать (или высказывание, которое доказывается или опровергается в процессе доказывания и опровержения)
· Аргументы (или основания) — истинные суждения, из которых следует тезис (или высказывания используемые для установления истинности или ложности тезиса при его доказывании или опровержении).
В качестве оснований в доказательствах или опровержениях могут использоваться высказывания о фактах, о данных опыта, высказывания, истинность которых обоснована ранее, в частности, доказанные ранее теоремы, законы науки, различного рода определения, аксиомы, постулаты, принципы и т.д.
· Форма (или демонстрация, методы и способы доказывания опровержения) — умозаключение связывающее аргументы с тезисом (или совокупность логических операций, в частности правил дедуктивных умозаключений, применяемых к тезису и основаниям с целью доказать или опровергнуть тезис).
Назначение демонстрации — сделать доказательство или опровержение убедительным не только по содержанию, но и объективно необходимым. Демонстрация призвана доказать, что между основаниями и доказываемым тезисом действительно было установлено отношение логического следования, в случае доказательства, или установленно его отсутствие в случае опровержения.
Виды доказательств:
1) Прямые (истинность тезиса непосредственно следует из истинности аргумента)
2) Косвенные:
· апагогическое — доказательство от противного
· разделительное — доказательство, где тезис — одна из альтернатив разделительного суждения, причем в этом суждении должны быть перечислены все альтернативы, кроме одной, которая и является тезисом доказательства.
Доказательством в самом широком смысле следует называть логическую процедуру выявления или восстановления последовательности в рассуждении, целью которой является установление (подтверждение) истинности некоторого высказывания.
2. Соблюдается ли закон достаточного основания в следующем рассуждении:
Закон достаточного основания:
Достоверны лишь те суждения, относительно истинности которых могут быть приведены достаточные основания: Р истинно, так как истинно Q.
№24
1. Определение и структура доказательства
Доказательство — логическая процедура установления истинности какого-либо суждения при помощи других суждений, истинность которых уже установлена.
Состав доказательства:
· Тезис — суждение, истинность которого следует доказать (или высказывание, которое доказывается или опровергается в процессе доказывания и опровержения)
· Аргументы (или основания) — истинные суждения, из которых следует тезис (или высказывания используемые для установления истинности или ложности тезиса при при его доказывании или опровержении).
В качестве оснований в доказательствах или опровержениях могут использоваться высказывания о фактах, о данных опыта, высказывания, истинность которых обоснована ранее, в частности, доказанные ранее теоремы, законы науки, различного рода определения, аксиомы, постулаты, принципы и т.д.
· Форма (или демонстрация, методы и способы доказывания опровержения) — умозаключение связывающее аргументы с тезисом (или совокупность логических операций, в частности правил дедуктивных умозаключений, применяемых к тезису и основаниям с целью доказать или опровергнуть тезис).
Назначение демонстрации — сделать доказательство или опровержение убедительным не только по содержанию, но и объективно необходимым.
Доказательством в самом широком смысле следует называть логическую процедуру выявления или восстановления последовательности в рассуждении, целью которой является установление (подтверждение) истинности некоторого высказывания.
2. Проанализируйте состав следующего простого категорического силлогизма:
Структура простого категорического силлогизма:
M a P
S a M , где М — средний термин, а S и Р — крайние термины.
S a P
S – меньший термин ð меньшая посылка
З — больший термин ð большая посылка.
Аксиома силлогизма:
· Если объем одного термина полностью входит в объем второго, а объем второго полностью входит в объем третьего, то и объем первого полностью входит в объем третьего.
·  Если объем одного термина полностью входит в объем второго термина, а объем второго полностью исключается из объема третьего, но и объем первого полностью исключается из объема третьего
Если объем одного термина полностью входит в объем второго термина, а объем второго полностью исключается из объема третьего, но и объем первого полностью исключается из объема третьего
·  Все, что сказано о роде, сказано о виде и индивиде:
Все, что сказано о роде, сказано о виде и индивиде:
 M a P
M a P
S a M
S a P
· 
 Все, что не сказано о роде, не сказано о виде и индивиде:
Все, что не сказано о роде, не сказано о виде и индивиде:
 M е P
M е P
S a M
S е P
Распределенность терминов в простом суждении:
Термин суждения (субъект, предикат) считается распределенным, если в данном суждении он мыслится во всем объеме.
Правила распределенности:
· Субъект всегда распределен в общих и единичных суждениях.
· Предикат всегда распределен в отрицательных суждениях.
№25
1. Прямое и косвенное доказательство.
1) Прямые (истинность тезиса непосредственно следует из истинности аргумента)
2) Косвенные:
· апагогическое — доказательство от противного
· разделительное — доказательство, где тезис — одна из альтернатив разделительного суждения, причем в этом суждении должны быть