Тема 2. Случайные величины
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
РАЗДЕЛ 1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Тема 1. Случайные события
Вопрос 1. Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не менее четырех очков, равна…
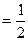
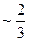
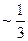

Вопрос 2. Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не менее трех очков, равна…


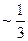

Вопрос 3. Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не менее двух очков, равна…

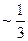
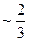

Вопрос 4. Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не более четырех очков, равна…




Вопрос 5. Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не более трех очков, равна…
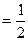
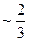
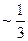

Вопрос 6. Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не более двух очков, равна…

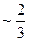


Вопрос 7. По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,3 и 0,25, соответственно. Тогда вероятность банкротства обоих предприятий равна…
= 0,075
~ 0,55
~ 0,75
~ 0,525
Вопрос 8. По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,1 и 0,05, соответственно. Тогда вероятность банкротства обоих предприятий равна…
= 0,005
~ 0,15
~ 0,05
~ 0,855
Вопрос 9. По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,1 и 0,25, соответственно. Тогда вероятность банкротства обоих предприятий равна…
= 0,025
~ 0,35
~ 0,25
~ 0,675
Вопрос 10. По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,1 и 0,35, соответственно. Тогда вероятность банкротства обоих предприятий равна…
= 0,035
~ 0,45
~ 0,35
~ 0,585
Вопрос 11. Из урны, в которой находятся 4 белых и 8 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…




Вопрос 12. Из урны, в которой находятся 4 белых и 7 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…


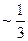

Вопрос 13. Из урны, в которой находятся 4 белых и 9 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…




Вопрос 14. Из урны, в которой находятся 5 белых и 8 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…




Вопрос 15. Из урны, в которой находятся 5 белых и 9 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна…


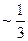

Вопрос 16. Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,5 и 0,4 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…
= 0,2
~ 0,9
~ 0,16
~ 0,3
Вопрос 17. Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,7 и 0,2, соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…
= 0,14
~ 0,9
~ 0,12
~ 0,24
Вопрос 18. Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,8 и 0,1, соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…
= 0,08
~ 0,9
~ 0,07
~ 0,18
Вопрос 19. Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,5 и 0,3, соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна…
= 0,15
~ 0,8
~ 0,12
~ 0,35
Вопрос 20. В первой урне 4 белых и 6 черных шаров. Во второй урне 1 белый и 9 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
= 0,25
~ 0,5
~ 0,3
~ 0,15
Вопрос 21. В первой урне 2 черных и 8 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
= 0,55
~ 0,11
~ 0,6
~ 0,25
Вопрос 22. В первой урне 1 черный и 9 белых шаров. Во второй урне 4 белых и 6 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
= 0,65
~ 0,13
~ 0,7
~ 0,25
Вопрос 23. В первой урне 5 белых и 5 черных шаров. Во второй урне 3 черных и 7 белых шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
= 0,6
~ 0,12
~ 0,65
~ 0,1
Вопрос 24. В первой урне 2 белых и 8 черных шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна…
= 0,25
~ 0,05
~ 0,3
~ 0,5
Вопрос 25. Из урны, в которой имеется 3 белых, 4 черных и 3 красных шаров, наудачу берут один шар. Какова вероятность того, что этот шар красный?



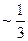
Вопрос 26. В шахматном турнире участвуют 10 шахматистов, из них 6 наиболее сильные. По жребию все участники делятся на две группы по 5 человек в каждой. Определить вероятность того, что сильные игроки делятся поровну.




Вопрос 27. Три стрелка независимо друг от друга производят по одному выстрелу. Их вероятности попадания в цель равны, соответственно, 0,5; 0,7; 0,9. Определить вероятность хотя бы одного попадания.
~ 0,85
~ 0,915
= 0,985
~ 0,915
Вопрос 28. Три стрелка независимо друг от друга производят по одному выстрелу. Их вероятности попадания в цель равны, соответственно, 0,5; 0,7; 0,8. Определить вероятность хотя бы одного попадания.
~ 0,35
~ 0,63
~ 0,45
= 0,97
Вопрос 29. Три стрелка независимо друг от друга производят по одному выстрелу. Их вероятности попадания в цель равны, соответственно, 0,5; 0,7; 0,6. Определить вероятность хотя бы одного попадания.
~ 0,75
= 0,94
~ 0,915
~ 0,985
Вопрос 30. В урне имеются 4 красных и 4 черных шаров. Из урны наугад извлекаются 3 шара. Определить вероятность того, что все они красные.




Вопрос 31. В урне имеются 5 красных и 5 черных шаров. Из урны наугад извлекаются 3 шара. Определить вероятность того, что все они красные.




Вопрос 32. В ящике имеется 10 деталей; из них 7 деталей первого сорта и 3 детали второго сорта. Из ящика наугад берутся 4 детали. Какова вероятность того, что среди них не будет ни одной детали второго сорта?
~ 0,25
~ 0,15
= 0,17
~ 0,4
Вопрос 33. В ящике имеется 10 деталей; из них 6 деталей первого сорта и 4 детали второго сорта. Из ящика наугад берутся 4 детали. Какова вероятность того, что среди них не будет ни одной детали второго сорта?




Вопрос 34. Прибор состоит из двух дублирующих друг друга элементов. Вероятность безотказной работы первого элемента равна 0,8, второго – 0,7. Определить вероятность безотказной работы прибора.
~ 0,54
~ 0,8
= 0,94
~ 0,7
Вопрос 35. Прибор состоит из двух дублирующих друг друга элементов. Вероятность безотказной работы первого элемента равна 0,9, второго – 0,6. Определить вероятность безотказной работы прибора.
~ 0,54
~ 0,6
= 0,96
~ 0,9
Вопрос 36. Прибор состоит из двух дублирующих друг друга элементов. Вероятность безотказной работы первого элемента равна 0,7, второго – 0,6. Определить вероятность безотказной работы прибора.
~ 0,42
= 0,88
~ 0,6
~ 0,7
Вопрос 37. В одной урне имеется 6 белых и 4 черных шаров, а во второй 4 белых и 6 черных шаров. Из каждой урны извлекается по одному шару. Какова вероятность того, что будет извлечен хотя бы один белый шар?
~ 0,55
~ 0,66
= 0,76
~ 0,82
Вопрос 38. В одной урне имеется 4 белых и 6 черных шаров, а во второй 7 белых и 3 черных шаров. Из каждой урны извлекается по одному шару. Какова вероятность того, что будет извлечен хотя бы один белый шар?
~ 0,76
~ 0,8
~ 0,95
= 0,82
Вопрос 39. В одной урне имеется 7 белых и 3 черных шаров, а во второй 6 белых и 4 черных шаров. Из каждой урны извлекается по одному шару. Какова вероятность того, что будет извлечен хотя бы один белый шар?
~ 0,76
= 0,88
~ 0,79
~ 0,92
Вопрос 40. В одной урне имеется 3 белых и 7 черных шаров, а во второй 6 белых и 4 черных шаров. Из каждой урны извлекается по одному шару. Какова вероятность того, что будет извлечен хотя бы один белый шар?
~ 0,58
= 0,72
~ 0,66
~ 0,88
Вопрос 41. В одной урне имеется 7 белых и 3 черных шаров, а во второй 3 белых и 7 черных шаров. Из каждой урны извлекается по одному шару. Какова вероятность того, что будет извлечен хотя бы один белый шар?
~ 0,58
= 0,79
~ 0,82
~ 0,9
Вопрос 42. В одной урне имеется 4 белых и 6 черных шаров, а во второй 3 белых и 7 черных шаров. Из каждой урны извлекается по одному шару. Какова вероятность того, что будет извлечен хотя бы один белый шар?
~ 0,45
~ 0,55
= 0,58
~ 0,7
Вопрос 43. Вероятность выхода из строя за время t лампы Л1 равна 0,1, лампы Л2 – 0,3, лампы Л3 – 0,4. Определить вероятность того, что хотя бы одна лампа будет гореть, если лампы включены параллельно.
~ 0,99
= 0,988
~ 0,985
~ 0,992
Вопрос 44. Вероятность выхода из строя за время t лампы Л1 равна 0,1, лампы Л2 – 0,2, лампы Л3 – 0,4. Определить вероятность того, что хотя бы одна лампа будет гореть, если лампы включены параллельно.
~ 0,988
= 0,992
~ 0,985
~ 0,99
Вопрос 45. Вероятность выхода из строя за время t лампы Л1 равна 0,1, лампы Л2 – 0,3, лампы Л3 – 0,5. Определить вероятность того, что хотя бы одна лампа будет гореть, если лампы включены параллельно.
= 0,985
~ 0,988
~ 0,992
~ 0,99
Вопрос 46. Вероятность выхода из строя за время t лампы Л1 равна 0,1, лампы Л2 – 0,2, лампы Л3 – 0,5. Определить вероятность того, что хотя бы одна лампа будет гореть, если лампы включены параллельно.
~ 0,98
~ 0,88
~ 0,91
= 0,99
Вопрос 47. Имеются две одинаковых урны. В первой урне находятся 6 белых и 4 черных шаров, во второй – 4 белых и 6 черных шаров. Из одной наугад выбранной урны извлекается один шар. Определить вероятность того, что шар черный.
~ 0,35
~ 0,45
= 0,5
~ 0,68
Вопрос 48. Имеются две одинаковых урны. В первой урне находятся 4 белых и 6 черных шаров, во второй – 7 белых и 3 черных шаров. Из одной наугад выбранной урны извлекается один шар. Определить вероятность того, что шар черный.
~ 0,35
= 0,45
~ 0,5
~ 0,65
Вопрос 49. Имеются две одинаковых урны. В первой урне находятся 4 белых и 6 черных шаров, во второй – 3 белых и 7 черных шаров. Из одной наугад выбранной урны извлекается один шар. Определить вероятность того, что шар черный.
~ 0,35
~ 0,45
~ 0,5
= 0,65
Вопрос 50. Имеются две одинаковых урны. В первой урне находятся 6 белых и 4 черных шаров, во второй – 3 белых и 7 черных шаров. Из одной наугад выбранной урны извлекается один шар. Определить вероятность того, что шар черный.
~ 0,35
~ 0,45
= 0,55
~ 0,65
Вопрос 51. Имеются две одинаковых урны. В первой урне находятся 7 белых и 3 черных шаров, во второй – 3 белых и 7 черных шаров. Из одной наугад выбранной урны извлекается один шар. Определить вероятность того, что шар черный.
~ 0,35
~ 0,4
= 0,5
~ 0,55
Вопрос 52. Имеются две одинаковых урны. В первой урне находятся 7 белых и 3 черных шаров, во второй – 6 белых и 4 черных шаров. Из одной наугад выбранной урны извлекается один шар. Определить вероятность того, что шар черный.
~ 0,3
= 0,35
~ 0,45
~ 0,5
Вопрос 53. Имеются три одинаковых урны. В первой урне находятся 6 белых и 4 черных шаров, во второй – 7 белых и 3 черных шаров, в третьей – 5 белых и 5 черных шаров. Из одной наугад выбранной урны извлекается один шар. Определить вероятность того, что шар будет белый.
~ 0,4
~ 0,5
= 0,6
~ 0,7
Вопрос 54. Имеются три одинаковых урны. В первой урне находятся 6 белых и 4 черных шаров, во второй – 3 белых и 7 черных шаров, в третьей – 5 белых и 5 черных шаров. Из одной наугад выбранной урны извлекается один шар. Определить вероятность того, что шар будет белый.
~ 0,4
= 0,47
~ 0,55
~ 0,6
Вопрос 55. Имеются три одинаковых урны. В первой урне находятся 4 белых и 6 черных шаров, во второй – 7 белых и 3 черных шаров, в третьей – 5 белых и 5 черных шаров. Из одной наугад выбранной урны извлекается один шар. Определить вероятность того, что шар будет белый.
~ 0,4
~ 0,47
= 0,53
~ 0,6
Вопрос 56. Имеются три одинаковых урны. В первой урне находятся 4 белых и 6 черных шаров, во второй – 3 белых и 7 черных шаров, в третьей – 5 белых и 8 черных шаров. Из одной наугад выбранной урны извлекается один шар. Определить вероятность того, что шар будет белый.
= 0,4
~ 0,47
~ 0,53
~ 0,6
Вопрос 57. Имеются три одинаковых урны. В первой урне находятся 6 белых и 4 черных шаров, во второй – 7 белых и 3 черных шаров, в третьей – 5 белых и 5 черных шаров. Из одной наугад выбранной урны извлекается один шар. Определить вероятность того, что шар будет черный.
~ 0,47
~ 0,53
~ 0,6
= 0,4
Вопрос 58. Имеются три одинаковых урны. В первой урне находятся 6 белых и 4 черных шаров, во второй – 3 белых и 7 черных шаров, в третьей – 5 белых и 5 черных шаров. Из одной наугад выбранной урны извлекается один шар. Определить вероятность того, что шар будет черный.
~ 0,4
~ 0,47
= 0,53
~ 0,6
Вопрос 59. Имеются три одинаковых урны. В первой урне находятся 4 белых и 6 черных шаров, во второй – 7 белых и 3 черных шаров, в третьей – 5 белых и 5 черных шаров. Из одной наугад выбранной урны извлекается один шар. Определить вероятность того, что шар будет черный.
= 0,47
~ 0,53
~ 0,6
~ 0,4
Вопрос 60. Имеются три одинаковых урны. В первой урне находятся 4 белых и 6 черных шаров, во второй – 3 белых и 7 черных шаров, в третьей – 5 белых и 5 черных шаров. Из одной наугад выбранной урны извлекается один шар. Определить вероятность того, что шар будет черный.
~ 0,4
~ 0,5
= 0,6
~ 0,7
Вопрос 61. Имеются две урны. В первой урне – 6 белых и 4 черных шаров; во второй – 7 белых и 3 черных шаров. Из первой урны во вторую, не глядя, перекладывается 1 шар. Шары во второй урне тщательно перемешиваются и из нее берется наугад один шар. Найти вероятность того, что шар белый.
~ 0,33
~ 0,67
= 0,69
~ 0,31
Вопрос 62. Имеются две урны. В первой урне – 6 белых и 4 черных шаров; во второй – 3 белых и 7 черных шаров. Из первой урны во вторую, не глядя, перекладывается 1 шар. Шары во второй урне тщательно перемешиваются и из нее берется наугад один шар. Найти вероятность того, что шар белый.
~ 0,69
~ 0,67
= 0,33
~ 0,31
Вопрос 63. Имеются две урны. В первой урне – 4 белых и 6 черных шаров; во второй – 7 белых и 3 черных шаров. Из первой урны во вторую, не глядя, перекладывается 1 шар. Шары во второй урне тщательно перемешиваются и из нее берется наугад один шар. Найти вероятность того, что шар белый.
~ 0,33
~ 0,31
= 0,67
~ 0,69
Вопрос 64. Имеются две урны. В первой урне – 4 белых и 6 черных шаров; во второй – 3 белых и 7 черных шаров. Из первой урны во вторую, не глядя, перекладывается 1 шар. Шары во второй урне тщательно перемешиваются и из нее берется наугад один шар. Найти вероятность того, что шар белый.
~ 0,69
~ 0,67
= 0,31
~ 0,33
Вопрос 65. Имеются две урны. В первой урне – 6 белых и 4 черных шаров; во второй – 7 белых и 3 черных шаров. Из первой урны во вторую, не глядя, перекладывается 1 шар. Шары во второй урне тщательно перемешиваются и из нее берется наугад один шар. Найти вероятность того, что шар черный.
~ 0,69
~ 0,67
~ 0,33
= 0,31
Вопрос 66. Имеются две урны. В первой урне – 6 белых и 4 черных шаров; во второй – 3 белых и 7 черных шаров. Из первой урны во вторую, не глядя, перекладывается 1 шар. Шары во второй урне тщательно перемешиваются и из нее берется наугад один шар. Найти вероятность того, что шар черный.
~ 0,31
~ 0,33
= 0,67
~ 0,69
Вопрос 67. Имеются две урны. В первой урне – 4 белых и 6 черных шаров; во второй – 7 белых и 3 черных шаров. Из первой урны во вторую, не глядя, перекладывается 1 шар. Шары во второй урне тщательно перемешиваются и из нее берется наугад один шар. Найти вероятность того, что шар черный.
~ 0,31
= 0,33
~ 0,67
~ 0,69
Вопрос 68. Имеются две урны. В первой урне – 4 белых и 6 черных шаров; во второй – 3 белых и 7 черных шаров. Из первой урны во вторую, не глядя, перекладывается 1 шар. Шары во второй урне тщательно перемешиваются и из нее берется наугад один шар. Найти вероятность того, что шар черный.
~ 0,31
~ 0,33
~ 0,67
= 0,69
Вопрос 69. Стрелок попадает в цель с вероятностью 0,5. Какова вероятность того, что в результате трех независимых выстрелов будет хотя бы одно попадание?
~ 0,936
~ 0,973
= 0,875
~ 0,999
Вопрос 70. Стрелок попадает в цель с вероятностью 0,6. Какова вероятность того, что в результате трех независимых выстрелов будет хотя бы одно попадание?
= 0,936
~ 0,973
~ 0,875
~ 0,999
Вопрос 71. Стрелок попадает в цель с вероятностью 0,7. Какова вероятность того, что в результате трех независимых выстрелов будет хотя бы одно попадание?
~ 0,936
= 0,973
~ 0,875
~ 0,999
Вопрос 72. Стрелок попадает в цель с вероятностью 0,8. Какова вероятность того, что в результате трех независимых выстрелов будет хотя бы одно попадание?
~ 0,936
~ 0,973
= 0,992
~ 0,875
Вопрос 73. Стрелок попадает в цель с вероятностью 0,9. Какова вероятность того, что в результате трех независимых выстрелов будет хотя бы одно попадание?
~ 0,936
~ 0,875
= 0,999
~ 0,992
Вопрос 74. Сколько раз необходимо бросить игральную кость, чтобы с вероятностью не менее 0,9 можно было ожидать появления хотя бы одной шестерки?
~ ≥11
~ ≥12
= ≥ 13
~ ≥26
Вопрос 75. Сколько раз необходимо бросить игральную кость, чтобы с вероятностью не менее 0,99 можно было ожидать появления хотя бы одной шестерки?
~ ≥12
~ ≥13
= ≥26
~ ≥38
Вопрос 76. Сколько раз необходимо бросить игральную кость, чтобы с вероятностью не менее 0,999 можно было ожидать появления хотя бы одной шестерки?
~ ≥13
= ≥38
~ ≥26
~ ≥12
Вопрос 77. Вероятность попадания в мишень при одном выстреле равна 0,5. Сколько необходимо произвести выстрелов, чтобы с вероятностью более 0,9 попасть в мишень хотя бы один раз?
~ ≥2
~ ≥3
= ≥4
~ ≥5
Вопрос 78. Вероятность попадания в мишень при одном выстреле равна 0,8. Сколько необходимо произвести выстрелов, чтобы с вероятностью более 0,9 попасть в мишень хотя бы один раз?
= ≥2
~ ≥3
~ ≥4
~ ≥5
Вопрос 79. Орудие производит 3 независимых выстрела по цели. Вероятность попадания снаряда в цель при одном выстреле равна 0,8. При одном попадании цель поражается с вероятностью 0,1, при двух попаданиях – с вероятностью 0,3 и при трех – с вероятностью 0,8. Определить вероятность поражения цели.
~ 0,66
= 0,53
~ 0,57
~ 0,65
Вопрос 80. Орудие производит 3 независимых выстрела по цели. Вероятность попадания снаряда в цель при одном выстреле равна 0,9. При одном попадании цель поражается с вероятностью 0,1, при двух попаданиях – с вероятностью 0,3 и при трех – с вероятностью 0,8. Определить вероятность поражения цели.
~ 0,53
~ 0,57
= 0,66
~ 0,65
Вопрос 81. Вероятность появления события А в 10 независимых испытаниях, проводимых по схеме Бернулли, равна 0,7. Тогда дисперсия числа появлений этого события равна…
= 2,1
~ 7
~ 0,21
~ 0,07
Вопрос 82. Вероятность появления события А в 10 независимых испытаниях, проводимых по схеме Бернулли, равна 0,4. Тогда дисперсия числа появлений этого события равна…
= 2,4
~ 6
~ 0,24
~ 0,06
Вопрос 83. Вероятность появления события А в 10 независимых испытаниях, проводимых по схеме Бернулли, равна 0,5. Тогда дисперсия числа появлений этого события равна…
= 2,5
~ 5
~ 0,25
~ 0,05
Вопрос 84. Вероятность появления события А в 10 независимых испытаниях, проводимых по схеме Бернулли, равна 0,8. Тогда дисперсия числа появлений этого события равна…
= 1,6
~ 8
~ 0,16
~ 0,08
Вопрос 85. Вероятность появления события А в 10 независимых испытаниях, проводимых по схеме Бернулли, равна 0,9. Тогда дисперсия числа появлений этого события равна…
= 0,9
~ 9
~ 0,19
~ 0,09
Тема 2. Случайные величины
Вопрос 86. Случайная величина Т характеризуется следующим распределением вероятностей:
| ti | -3 | -2 | 0 | 1 | 3 |
| P i | 0,2 | 0,1 | 0,2 | 0,4 | 0,1 |
Определить вероятность события (-2 ≤ Т < 2).
~ 0,6
= 0,7
~ 0,8
~ 0,9
Вопрос 87. Дана функция распределения случайной величины Z:

Найти вероятность события (1 ≤ Z < 2).
~ 0,11
= 0,13
~ 0,15
~ 0,17
Вопрос 88. Случайная величина Х имеет функцию распределения:

Найти вероятность события (1 ≤ X < 2).
~ 0,11
= 0,75
~ 0,15
~ 0,17
Вопрос 89. Функция распределения случайной величины Х задана выражением:

Вычислить P (4 ≤ X < 5).
~ 0,1
= 0,2
~ 0,25
~ 0,35
Вопрос 90. Плотность распределения случайной величины Х задана выражением:

Найти среднее квадратическое отклонение случайной величины Х.
~ 0,1
~ 0,15
= 0,2
~ 0,23
Вопрос 91. Дан закон распределения вероятностей дискретной случайной величины X:

Тогда значение a равно…
= 0,3
~ 0,7
~ (-0,7)
~ 0,4
Вопрос 92. Дан закон распределения вероятностей дискретной случайной величины X:

Тогда значение a равно…
= 0,2
~ 0,8
~ (-0,8)
~ 0,1
Вопрос 93. Дан закон распределения вероятностей дискретной случайной величины X:

Тогда значение a равно…
= 0,6
~ 0,4
~ (-0,4)
~ 0,5
Вопрос 94. Дан закон распределения вероятностей дискретной случайной величины X:

Тогда значение a равно…
= 0,2
~ 0,8
~ (-0,8)
~ 0,1
Вопрос 95. Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:

Тогда математическое ожидание этой случайной величины равно…
= 2,6
~ 4
~ 3,4
~ 2
Вопрос 96. Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:

Тогда математическое ожидание этой случайной величины равно…
= 1,6
~ 1
~ 2,6
~ 0,5
Вопрос 97. Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:

Тогда математическое ожидание этой случайной величины равно…
= 3,2
~ 5
~ 4
~ 2,5
Вопрос 98. Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:

Тогда математическое ожидание этой случайной величины равно…
= 4,4
~ 4,5
~ 4,6
~ 2
Вопрос 99. Пусть X – дискретная случайная величина, заданная законом распределения вероятностей:

Тогда математическое ожидание этой случайной величины равно…
= 3,8
~ 4
~ 4,2
~ 2