Подборка модели вида ARIMA (p,k,q) для ряда А

12
Далее ⇒

1.1 В первую очередь, протестируем ряд А на стационарность. Рассмотрим график временного ряда А:

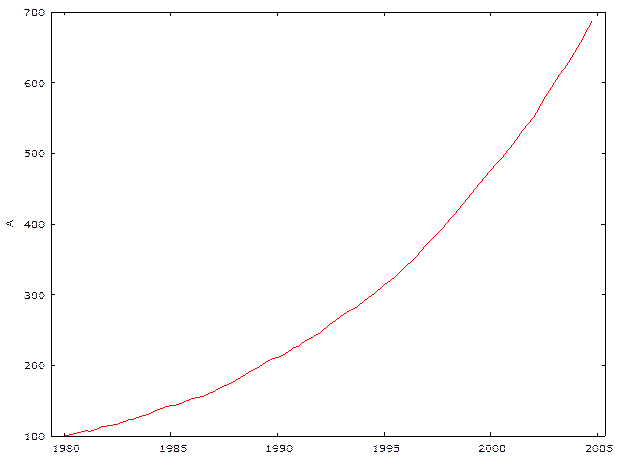
Уже на основании графика можем заключить, что исходный ряд не является стационарным. В качестве дополнительного подтверждения этой гипотезы, проведем расширенный тест Дики-Фуллера ряда А. Пусть порядок лага будет определен пакетом Gretl автоматически, пусть будет учтена константа и тренд. В результате получим следующее:

Тест Дики-Фуллера для A

объем выборки 99

нулевая гипотеза единичного корня: a = 1

тест с константой

модель: (1-L)y = b0 + (a-1)*y(-1) + e

коэф. автокорреляции 1-го порядка для e: 0,068

оценка для (a - 1): 0,0202285

тестовая статистика: tau_c(1) = 30,1664

P-значение 1

с константой и трендом

модель: (1-L)y = b0 + b1*t + (a-1)*y(-1) + ... + e

коэф. автокорреляции 1-го порядка для e: -0,009

лаг для разностей: F(9, 78) = 0,685 [0,7202]

оценка для (a - 1): 0,0225823

тестовая статистика: tau_ct(1) = 3,38825

асимпт. р-значение 1

Поскольку P-value = 1 превышает любой разумный уровень значимости, делаем вывод, что гипотеза Но теста Дики-Фуллера (гипотеза о нестационарности ряда) принимается, и ряд А не является стационарным.

Перейдем к первым разностям ряда и рассмотрим новый временной ряд d_A. График этого временного ряда имеет вид:

На основании этого графика также можем сделать вывод о том, что процесс d_A не является стационарным. Для подтверждения этого вывода, снова проведем тест Дики-Фуллера и получим следующее:

Расширенный тест Дики-Фуллера для d_A

включая 6 лага(-ов) для (1-L)d_A (максимальное значение равно 12)

объем выборки 92

нулевая гипотеза единичного корня: a = 1

тест с константой

модель: (1-L)y = b0 + (a-1)*y(-1) + ... + e

коэф. автокорреляции 1-го порядка для e: 0,005

лаг для разностей: F(6, 84) = 9,077 [0,0000]

оценка для (a - 1): 0,0618306

тестовая статистика: tau_c(1) = 1,49658

асимпт. р-значение 0,9993

с константой и трендом

модель: (1-L)y = b0 + b1*t + (a-1)*y(-1) + ... + e

коэф. автокорреляции 1-го порядка для e: -0,056

лаг для разностей: F(5, 85) = 1,698 [0,1440]

оценка для (a - 1): -0,319884

тестовая статистика: tau_ct(1) = -1,76781

асимпт. р-значение 0,7205

P-value по прежнему превышает любой разумный уровень значимости, и гипотеза Но теста Дики-Фуллера снова принимается: ряд d_A не является стационарным. Поэтому, перейдем ко вторым разностям ряда А, рассмотрим новый временной ряд d_d_A. Рассмотрим график ряда d_d_A:

На основании представленного графика можем сделать первичное предположение о том, что ряд является стационарным. Подтвердим данное предположение результатами теста Дики-Фуллера для временного ряда d_d_A:

Расширенный тест Дики-Фуллера для d_d_A

включая 4 лага(-ов) для (1-L)d_d_A (максимальное значение равно 12)

объем выборки 93

нулевая гипотеза единичного корня: a = 1

тест с константой

модель: (1-L)y = b0 + (a-1)*y(-1) + ... + e

коэф. автокорреляции 1-го порядка для e: -0,049

лаг для разностей: F(4, 87) = 7,583 [0,0000]

оценка для (a - 1): -3,40646

тестовая статистика: tau_c(1) = -7,17745

асимпт. р-значение 1,088e-010

с константой и трендом

модель: (1-L)y = b0 + b1*t + (a-1)*y(-1) + ... + e

коэф. автокорреляции 1-го порядка для e: 0,005

лаг для разностей: F(5, 84) = 7,100 [0,0000]

оценка для (a - 1): -4,19552

тестовая статистика: tau_ct(1) = -6,92063

асимпт. р-значение 4,208e-009

Поскольку в данном случае P-value = 1,088e-10 < 0,01 (а также меньше любого другого разумного уровня значимости), делаем вывод, что гипотеза Но теста Дики-Фуллера о нестационарности ряда отклоняется, и ряд d_d_A является стационарным.

Нестационарный процесс А удалось свести к стационарному процессу d_d_A, и именно с этим процессом мы продолжим работу в следующих пунктах.

1.2. Сделаем первые предположения о виде ряда на основании его коррелограммы. Коррелограмма ряда d_d_A (пусть максимальное число лагов составит 20) имеет следующий вид:

Вид ACF ряда наводит на мысль о том, что ряд d_d_A является МА процессом первого порядка (поскольку есть только одно, первое, значение функции ACF, статистически значимо отличное от нуля).

1.3. Попробуем непосредственно построить модель. В первую очередь проверим предположение того, что ряд А описывается моделью ARIMA (0,2,1), или ряд d_d_A описывается моделью ARIMA (0,0,1) = MA (1):

Модель 1: ARMA, использованы наблюдения 1980:3-2004:4 (T = 98)

Зависимая переменная: d_d_A

Стандартные ошибки рассчитаны на основе Гессиана

Коэффициент Ст. ошибка z P-значение

const 0,118343 0,0217786 5,4339 <0,00001 ***

theta_1 -0,825297 0,0582614 -14,1654 <0,00001 ***

Среднее зав. перемен 0,124087 Ст. откл. зав. перемен 1,484416

Среднее инноваций -0,014903 Ст. откл. инноваций 1,170854

Лог. правдоподобие -155,0853 Крит. Акаике 316,1706

Крит. Шварца 323,9255 Крит. Хеннана-Куинна 319,3073

Действительная часть Мнимая часть Модуль Частота

MA Корень 1 1,2117 0,0000 1,2117 0,0000

Обратим внимание на то, что в полученной модель характеризуется приемлемыми значениями критерия каике и Шварца, а также хороша значимостью константы и первого лага МА-составляющей модели.

На построение именно этой модели нас натолкнул вид коллерограммы ряда d_d_A. Чтобы убедиться, что полученная модель хороша, обратим внимание на то, что добавление лагов AR-составляющей и дополнительных лагов MA-составляющей модели не улучшает ее характеристик. Например, попробуем описать ряд d_d_A моделью ARMA (2,0,2):

Модель 2: ARMA, использованы наблюдения 1980:3-2004:4 (T = 98)

Зависимая переменная: d_d_A

Стандартные ошибки рассчитаны на основе Гессиана

Коэффициент Ст. ошибка z P-значение

const 0,118738 0,0232806 5,1003 <0,00001 ***

phi_1 0,356885 0,64692 0,5517 0,58118

phi_2 -0,177353 0,123524 -1,4358 0,15107

theta_1 -1,12246 0,652809 -1,7194 0,08554 *

theta_2 0,279339 0,554187 0,5041 0,61423

Среднее зав. перемен 0,124087 Ст. откл. зав. перемен 1,484416

Среднее инноваций -0,011494 Ст. откл. инноваций 1,157414

Лог. правдоподобие -153,9798 Крит. Акаике 319,9595

Крит. Шварца 335,4693 Крит. Хеннана-Куинна 326,2329

Действительная часть Мнимая часть Модуль Частота

AR Корень 1 1,0061 -2,1508 2,3745 -0,1804

Корень 2 1,0061 2,1508 2,3745 0,1804

MA Корень 1 1,3333 0,0000 1,3333 0,0000

Корень 2 2,6850 0,0000 2,6850 0,0000

Модель (2) уступает модели (1) по всем показателям качества: во-первых, критерии Шварца и Акаике здесь выше, во-вторых, в модели появилось несколько незначимых лагов. Поэтому, будем отдавать предпочтение модели (1).

Попробуем улучшить модель (1), прибегая к учету сезонности. Добавим первую разность сезонной компоненты и первый порядок МА. Получим модель (3):

Модель 3: ARIMA, использованы наблюдения 1981:3-2004:4 (T = 94)

Зависимая переменная: (1-Ls) d_d_A

Стандартные ошибки рассчитаны на основе Гессиана

Коэффициент Ст. ошибка z P-значение

const 0,00731114 0,00119846 6,1004 <0,00001 ***

theta_1 -1 0,0532804 -18,7686 <0,00001 ***

Theta_1 -0,999986 0,216516 -4,6185 <0,00001 ***

Среднее зав. перемен 0,038700 Ст. откл. зав. перемен 1,995767

Среднее инноваций 0,019520 Ст. откл. инноваций 1,087806

Лог. правдоподобие -151,9717 Крит. Акаике 311,9435

Крит. Шварца 322,1166 Крит. Хеннана-Куинна 316,0527

Действительная часть Мнимая часть Модуль Частота

MA Корень 1 1,0000 0,0000 1,0000 0,0000

MA (сезонные) Корень 1 1,0000 0,0000 1,0000 0,0000

При переходе к модели (3) критерии Шварца и Акаике дополнительно снизились в сравнении с моделью (1), к тому же, дополнительно учтенная сезонная компонента оказался значимой на 1%м уровне. Останавливаясь на модели (3), обратим также внимание на график коррелограммы остатков (при рассмотрении 20 лагов):

Все представленные остатки статистически незначимо отличаются от нуля, а значит, остатки данной модели описываются процессом белого шума, как и должно быть. Будем считать, что модель (3), модель ARIMA (0,2,1) для ряда А, является наиболее удачной. Ряд А будет описываться регрессией следующего вида:

12
Далее ⇒