Колмогоров Андрей Николаевич
КРАТКИЙ КУРС ТЕОРИИ ВЕРОЯТНОСТЕЙ
и ВВЕДЕНИЕ В МАТЕМАТИЧЕСКУЮ СТАТИСТИКУ
Часть 1. СЛУЧАЙНЫЕ СОБЫТИЯ
Введение
События бывают случайные и неслучайные (детерминированные, закономерные). Попробуем привести примеры неслучайных явлений, процессов, свободных от неожиданностей. Полет самолета на автопилоте (J без вмешательства птиц и ракет) на заданной высоте можно считать строго горизонтальным. Хотя фактически происходят отклонения центра массы от прямой и колебания самолета вокруг центра масс из-за турбулентности атмосферы.
Постоянно ли напряжение в сети? Возьмем 10 одинаковых лампочек. Проработают ли они одинаковое время? J Закономерна ли наша встреча здесь и сейчас, особенно если вспомнить о выборе специальности, сдаче сессии, транспорте и т.д.
Есть ли вообще явления, события, процессы свободные от вмешательства случайных факторов в той или иной форме?
Однако в ряде практических и тем более теоретических задач случайным элементом можно пренебречь, рассматривая упрощенную модель явления. Такая схема изучения явления называется детерминистской. Согласно этой схеме при решении любой задачи выделяются основные условия, выясняется на какие параметры они влияют. Затем применяется тот или иной матаппарат (например, составляется и решается система дифференциальных уравнений). Таким образом выясняется основная закономерность, свойственная данному явлению, и дающая возможность предсказать результат опыта по заданным начальным условиям. Это классический подход для точных наук – химии, физики, механики, техники.
Однако есть задачи, где результат опыта существенно зависит от столь большого количества факторов, что практически невозможно зарегистрировать и учесть их все.
VБросание 3 костей и ожидание выпадения 3 шестерок.
V Поведение молекулы газа в кубе. Если есть 1 молекула с заданной массой и скоростью, можно запрограммировать ее поведение. 2 молекулы. Сложнее. 3 молекулы. Еще сложнее и дольше. А 10000 молекул?
Вот здесь уже нужен вероятностный (статистический) подход. Цель вероятностных методов – в том, чтобы минуя слишком сложное (а иногда и невозможное) исследование отдельного явления, обратиться непосредственно к законам, управляющих массами таких явлений.
ТВ – это математическая теория, которая имеет свои инструменты исследования, которые мы рассмотрим в дальнейшем. В каких случаях их можно использовать?
ТВ не занимается изучением уникальных событий, которые не допускают повторений. ТВ занимается массовыми явлениями, т. е. явлениями, которые могут быть осуществлены большое количество раз в относительно неизменных условиях.
Рассмотрим электрические лампочки. У одной срок службы –2001 ч., у другой – 1500, третья перегорела сразу. Случайные события? Да. Можем применить аппарат ТВ? Как? Если мы будем наблюдать за 1000 лампочек, то обнаружим закономерность. Чем больше опытов, тем она виднее. Результаты будут группироваться относительно симметрично относительно некоторого среднего значения срока работы лампочки.
Практика показывает, что наблюдая массу однородных явлений, мы часто обнаруживаем в них своего рода устойчивости. Всем известно, что вероятность выпадения герба (и, соответственно, решки) – 0.5. Если мы кинем монетку 4 раза, обязательно ли герб выпадет дважды? А если 1000 раз? А больше? Чем больше – тем отношение числа выпавших гербов к общему числу бросаний будет ближе к 0.5. Частота рождения мальчиков в самых разных странах мира примерно 0.51. Частота встречаемых различных букв в больших текстах тоже различна и устойчива, на чем основаны некоторые методы расшифровки.
ТВ зародилась в 17 в. при разработке теории азартных игр с целью дать рекомендации игрокам. Затем эти методы стали применяться в практике первых страховых компаний для установления разумных страховых премий. Сегодня вероятностные методы широко применяются практически во всех отраслях науки, техники, экономики.
Случайные события
Под опытом (испытанием, экспериментом) понимается некоторая воспроизводимая совокупность условий , при которых наблюдается какое-либо явление (фиксируется тот или иной результат).
Случайное событие – такой результат опыта, который может либо произойти, либо нет.
Обычно слово «случайное» опускается. Просто «событие». (J Мы-то понимаем, что все они случаны.)
V Бросаем две кости (испытание). Сумма очков =11-случайное событие.
V Бросание стрел в дартс (испытание). Попадание – событие.
Для каждого испытания можно указать некоторую систему возможных исходов, обладающую тем свойством, что в результате испытания должен осуществиться один и только один исход. Такая система исходов, связанных с данным испытанием, называется пространством элементарных событий W, а входящие в него исходы элементарными событиями (исходами) 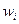 . Т.е. элементарный исход - простейший, неделимый результат испытания.
. Т.е. элементарный исход - простейший, неделимый результат испытания.
VИспытание – выборка шара с возвратом из урны, содержащей m белых и M-m черных шаров.
Возможные исходы: w1 – вытащен белый шар,
w2 – вытащен черный шар,
W=(w1, w2).
V Испытание – стрельба по мишени до первого попадания.
W=(w1, w2,…,wn…); wi – номер i-го попадания,
W – бесконечное счетное множество элементарных событий.
V Выстрел по мишени с гарантированным попаданием. Размером пули можно пренебречь. Ставим в соответствие каждой точке мишени q исход испытания w(q). W содержит несчетное бесчисленное множество элементарных событий.
Теперь мы можем определить случайное событие как множество элементарных исходов, которое является подмножеством W.
V Бросаем две кости (испытание). Сумма очков =11-случайное событие. Ему соответствуют два элементарных исхода -6:5 и 5:6.
Достоверное событие –событие, которое в результате испытания обязательно произойдет.
V Испытание: наугад называем цифру. Событие – названное число меньше 10
V Испытание: наугад вытаскиваем карту из колоды. Событие – карта либо красная, либо черная.
Невозможное событие - событие, которое в результате испытания никогда не произойдет. 
VПоявление 20 очков при бросании 3 костей
VНаугад выбранное число, состоящее из 2 и 1, кратно 5.
События называются несовместными, если появление одного из них исключает появление других в одном и том же испытании.
VИспытание: бросание монеты. Несовместные события: появление герба или решки.
V Испытание: стрельба по мишени. Несовместные события: попадание или промах.
События образуют полную группу, если в результате испытаний появляется хотя бы одно из них.
V Испытание: бросание кости.
События: 1) выпадение четного числа очков
2) выпадение 1
3) выпадение числа очков больше 2
образуют полную группу.
V Испытание: вытаскивание карты из колоды в 36 карт.
События: 1) карта с цифрой
2) картинка
3) красная карта
4) черная карта
образуют полную группу.
Отметим, что среди вышеперечисленных событий были совместные: например картинка и красная карта вполне совместны
В дальнейшем нас будет особо интересовать полная группа попарно несовместных событий (в результате испытания может произойти только одно событие).
V Испытание: вытаскивание из урны, в которой лежат белые, красные и синие шары, одного шара
События: 1) шар белый
2) шар красный
3) шар синий
образуют полную группу попарно несовместных событий.
События называются равновозможными , если по условиям симметрии есть основание считать , что ни одно из них не является более возможным чем другие.
VМонеты, кости, карты (Jне крапленые)
Понятие вероятности
Попытаемся определить понятие вероятности, которое интуитивно вроде бы ясно. Существуют три подхода к определению вероятности: классический, статистический, аксиоматический.
Классический подход к определению вероятности.
При классическом подходе рассматривается полная группа попарно несовместных равновозможных элементарных исходов.
VИспытание: вытаскивание из урны, в которой лежат белые и красные шары, одного шара
Элементарный исходы: 1) шар белый; 2) шар красный
V Испытание: бросание 2 костей.
Элементарные исходы:
1 ая кость 2 ая кость
n очков m очков
Всего 36 исходов.
Обозначим элементарные исходы 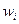
Событие А: сумма очков на двух костях = 4.
Элементарные исходы:  ,
,  ,
, 
Событию А благоприятствуют 3 элементарных исхода.
Событие В: сумма очков на двух костях <= 4.
Элементарные исходы:  ,
,  ,
, 
 ,
,  ,
, 
Событию В благоприятствуют 6 элементарных исходов.
Интуитивно понятно, что событие В более вероятно, чем А.
Вероятностью события А называется отношение числа благоприятствующих этому событию исходов  к общему числу элементарных исходов
к общему числу элементарных исходов  :
:
P(A)=  .
.
Свойства вероятности
1.Если А - достоверное Р(А)= 1 ; т.к. m= n
2. Если А – невозможное Р(А)= 0; т.к. m=0
3. Вероятность любого события А 0  Р(A)
Р(A)  всегда, т.к. 0
всегда, т.к. 0 
 .
.
Недостатки классического определения:
1. Требование конечного (в крайнем случае - счетного) числа элементарных исходов.
2. Требование симметрии опыта, т.е. равновозможности исходов.
Первый недостаток преодолевается путем введения геометрической вероятности.
Пусть на плоскости имеется область Q, в ней содержится подобласть  .
.
 В область Q наудачу бросается точка. Наудачу здесь значит, что брошенная точка может попасть в любую точку области Q; вероятность попадания в какую-либо часть области q пропорциональна площади этой фигуры и не зависит от ее формы и расположения внутри большой области. Вопрос: какова вероятность события А - что точка попадет в область q?
В область Q наудачу бросается точка. Наудачу здесь значит, что брошенная точка может попасть в любую точку области Q; вероятность попадания в какую-либо часть области q пропорциональна площади этой фигуры и не зависит от ее формы и расположения внутри большой области. Вопрос: какова вероятность события А - что точка попадет в область q?
P(A)=  - отношение площадей.
- отношение площадей.
V Q – круг радиусом 10см, q – круг радиусом 5см, P(A)= 
Определение геометрической вероятности обобщается на любую меру области (отрезок, объем и т.д.). Обозначив меру как mes, получим
Р(А) 
Таким образом, введением геометрической вероятности мы избавились от счетности (и, тем более, конечности) элементарных исходов. Но – увы!-требование равновозможности исходов никуда не делось.
Статистический подход к определению вероятности.
В задачах технического или естественнонаучного характера требование равновозможности исходов выполняется крайне редко. Классическим путем нельзя вывести вероятность распада атома радия за определенный период времени или определить вероятность рождения близнецов.
Пусть проводится серия из n опытов, в каждом из которых может случиться или не случиться событие А.
Относительной частотой называется отношение количества событий, где А произошло  , к общему числу опытов
, к общему числу опытов  :
:



Понятие частоты является основным при экспериментальном изучении случайных событий. Частота не может служить объективной характеристикой изучаемого случайного события, так как зависит от случайного стечения обстоятельств, связанных с данной серией испытаний, от индивидуальных особенностей самого экспериментатора.
Однако с увеличением числа испытаний частота становится «устойчивой». Теория вероятностей предназначена для описания случайных событий, обладающих устойчивой частотой. Вероятность случайного события соответствует в идеализированном виде тому пределу, к которому стремится устойчивая частота события при неограниченном увеличении числа испытаний.
Свойства вероятности, вытекающие из классического определения, сохраняются и при статистическом определении вероятности
1. Если А - достоверное  = 1 ; т.к. m= n
= 1 ; т.к. m= n
2. Если А – невозможное  = 0; т.к. m=0
= 0; т.к. m=0
3. Вероятность любого события А 0 

 всегда, т.к. 0
всегда, т.к. 0 
 .
.
Недостатки статистического определения вероятности: необходимо приводить большое (и, неизвестно насколько большое) число испытаний.
В чем принципиальная разница классического и статистического подходов? Классическую вероятность можно вычислить до испытания, да и самогоиспытания можно не проводить. Относительную частоту можно вычислить только после проведения испытания. (J до того и после того)
Соответствие между классическим и статистическим определениями было выявлено еще в период становления теории вероятностей как теории азартных игр. Было установлено, что при корректном использовании классического определения вероятность событий практически совпадает с их частотами при большом числе повторений эксперимента.
V J Есть кости и час времени. Нужно установить, нет ли свинца в шестерке. Как?
ДЕЙСТВИЯ НАД СЛУЧАЙНЫМИ СОБЫТИЯМИ
Прежде чем ввести аксиоматическое определение вероятности, рассмотрим, какие действия можно производить над событиями. Для простоты мы будем рассматривать классическую схему с равновозможными исходами.
Мы уже ввели понятие элементарного – простейшего, неделимого исхода испытания и определили, что множество всех элементарных исходов называется пространством элементарных исходов Ω.
V Испытание: подбрасывание 2 монет.

V Испытание: вытаскивание костяшки домино

Напомним, что случайное событие А - произвольное подмножество пространства элементарных исходов Ω (  ).
).
V Испытание: вытаскивание костяшки домино
Событие А: ٱ + ٱ ≥ 10 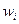 ={ |5|5|, |5|6|, |6|6|, |6|4|}
={ |5|5|, |5|6|, |6|6|, |6|4|} 
Событие B: ٱM 3 и ٱ M 3 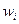 ={|3|3|,|3|6|,|6|3|,|6|6|}
={|3|3|,|3|6|,|6|3|,|6|6|} 
Событие C: ٱM 2 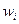 - много
- много 
Событие D: ٱ ≥ 0, ٱ ≥ 0 , D = Ω
Событие Е: ٱ + ٱ ≥ 15 E = Æ
Т. о. очевидно однозначное соответствие между множествами и событиями. Рассмотрим те события, определения которых мы уже дали.
| Множество | События | |
| Ω | Множество (универсум) | Пространство элементарных исходов |
| wiєΩ | Элемент множества | Элементарный исход |
| A Ì Ω | Подмножество | Событие |
| A = Ω | A = Ω | Достоверное событие |
| B = Æ | Æ | Невозможное событие |
Теперь рассмотрим действия над событиями, воспользовавшись диаграммами Эйлера-Венна.
Произведением двух событий А и В называется событие С, происходящее тогда и только тогда, когда одновременно происходят оба события А и В, т. е. состоящее из исходов, которые принадлежат и А и В.
С = АВ, С = АÇВ - пересечение.

V Испытание: вытаскивание костяшки домино
Событие А: ٱ + ٱ M 3
Событие В: ٱ + ٱ M 2
Событие С =АВ: ٱ + ٱM 6
События А и В называютсянесовместными, если их произведение является невозможным событием.
АВ = Æ, АÇВ = Æ

V Испытание: вытаскивание костяшки домино
Событие А: дубль
Событие В: ٱ + ٱ –нечетное число
Событие С =АВ=Æ
Суммой двух событийА и В называется событие С, происходящее тогда и только тогда, когда происходит хотя бы одно из событий А или В., т. е. С состоит из исходов которые принадлежат хотя бы одному из подмножеств А или В.
С = А + В,С = АÈВ
 |
Суммой нескольких событий называется событие, которое состоит в появлении хотя бы одного из этих событий.
JV Испытание: ожидание в тоске
Событие  : приходит Вася.
: приходит Вася.
Событие  : приходит Маша.
: приходит Маша.
Событие  : приходит куратор.
: приходит куратор.
Событие  : приходит декан.
: приходит декан.
Событие В: приходит хоть кто-нибудь 
Событием Ā, противоположным событию А называется событие, происходящее тогда и только тогда, когда не происходит А.
|
 А + Ā = Ω
А + Ā = Ω
V Испытание: вытаскивание костяшки домино
Событие А: дубльпусто
Событие Ā: все остальное
Аксиоматический подход к определению вероятности.
Любая уважающая себя точная наука имеет аксиоматическое построение. Т.е. вводятся неопределяемые аксиоматические понятия, формулируется система аксиом и на этой основе строятся основные определения, утверждения и теоремы. Классический еще школьный пример – эвклидова геометрия.
Теория вероятности вплоть до 30-ых годов прошлого века не считалась точной математической наукой, пока Колмогоров не поставил ее на строгую аксиоматическую основу. Аксиоматическое определение вероятности включает в себя как частные случаи классическое и статистическое определения и преодолевает недостатки каждого
Дадим популярное истолкование σ – алгебры событий. Рассмотрим следующий опыт: подбрасывание пирамиды с неравными гранями (и следовательно с неравновозможными исходами).
Пространство элементарных исходов Ω={w1, w2, w3, w4}, {w1}, {w2}, {w3},{w4} – выпадает грань с таким то номером. Любое событие АÌΩ. Сколько всего событий может быть ?
1. События, включающие в себя только один исход. Подчеркнем, что они неравновозможны.
{w1}, {w2}, {w3},{w4}
2. События, включающие в себя по 2 исхода (например, номер грани – четный ).
{w1, w2}, {w2, w3}, {w1, w3},{w2, w4},{w1, w4},{w3, w4}.
3. События включающие в себя по 3 исхода (например, номер грани <4 ).
{w1, w2, w3}, {w1, w2, w4}, {w2, w3, w4}, {w1, w3, w4}.
4. Событие, включающее в себя 4 исхода (например, номер грани <10 ).
{w1, w2, w3, w4} – Ω. Это достоверное событие
5. Событие, не включающее в себя ни одного исхода (например, номер грани >10 ).Это невозможное событие Æ.
Колмогоров Андрей Николаевич

1903-1987