Основная теорема двойст-ти

1. Если 1 из ДЗ имеет опт-ое реш-е, то др. также имеет опт-ое реш-е, причем Хопт=Uопт, Zmax=Wmin; 2. Если 1 из ДЗ неразреш-а по причине неогран-ти цел.функ., то др. задача не имеет допуст. реш-й

Решая 1 из ДЗ СМ в последней симплекс. табл.мы найдем реш-е и др. задачи. Для этого необ-о привести с-му к канон. форме к единич. базису (при этом св.чл м.б. «-») и записать соот-е во взаимосвяз-ые пары, т.е. бп ДЗ соот-т св.п ИЗ и наоборот. Зная соот-е перем-х по результатам последней симплекс.табл. ИЗ можно записать реш-е ДЗ, при этом: 1. перем-е ДЗ, соот-щие св. п послед.сим.табл. ИЗ, приравн-ся к оц-кам соот-щих св.п ИЗ; 2. перем-е ДЗ, соот-щие бп послед. сим.табл. ИЗ, приравн-ся к нулю.

ТРАНСПОРТНАЯ ЗАДАЧА

Транспортная задача - задача определения оптимального плана перевозок груза из данных пунктов отправления в заданные пункты потребления.

Методы нахождение опорного решения транспортной задачи.Исходные данные транспортной задачи задаются в распределительной таблице, где по строкам отражают запасы груза у каждого поставщика, а по столбцам - потребность в данном грузе каждого потребителя. В правом верхнем углу каждой клетки - стоимость перевозки единицы груза от каждого поставщика каждому потребителю.

С_ij – стоимость перевозки единицы груза, а_i – запас груза у i – го поставщика (i =1…m), b_i- потребность в грузе j- потребителя (j=1…n), х – кол-во груза от i-го поставщика к j –потребителю.

Постановка задачи (на мин-ую стоимость перевозки груза): найти значение переменных x_ij обеспечивающих целевой функции 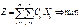и удовлетворяющих системе ограничений: 1. Сумма всех грузов перевезенных от i-поставщика д.б. равна запасу груза у этого поставщика. 2. Сумма всех грузов, доставляемых j- потребителю д.б. равна потребности этого потребителя. 3. Неотрицательность переменных. Т.е.:

1 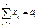i=1…m

2 j=1…n

3 x_ij 0 i=1…m, j=1…n

Причем, для того чтобы решить транспортную задачу, сумма запасов однородного груза у поставщиков должна быть равна сумме потребностей в этом грузе потребителей (закрытая модель).

В случае невыполнения этого условия (открытая модель) необходимо произвести некоторые преобразования (введениефиктивного поставщика илипотребителя) и получить закрытую модель.

Алгоритм решения транспортной задачи состоит из двух шагов:

- составление первоначального опорного плана каким-либо методом (минимального элемента в таблице, северо-западного угла, аппроксимации);

- улучшениеэтого плана и доведение его до оптимального методом потенциалов.

Рассмотрим алгоритм составления первоначального опорного плана методом аппроксимации. Данный метод особенно эффективен для задач малой размерностью, так как в большинстве случаев приводит к оптимальному решению.

В распределительной таблице добавляются нулевой столбец (слева) и нулевая строка (сверху).

В нулевую строку записываются разности, полученные в соответствующих столбцах путем вычитания наименьшей стоимости из следующей за ней по величине. В нулевой столбец заносят разности, полученные аналогично в строках. Из всех полученных разностей выбирается наибольшая. При этом могут встретиться два случая:

1. Одна наибольшая разность. Тогда в соответствующей строке (столбце) обычным образом заполняется клетка, в которой стоит наименьшая стоимость, и рассчитываются новые разности.

2. Несколько одинаковых наибольших разностей. В этом случае в соответствующей строке (столбце) находим клетку, в которой стоит наименьшая стоимость, и проверяем, будет ли этот показатель наименьшим в противоположном ряду.

Для строки противоположным рядом будем считать столбец, а для столбца - строку.

Здесь возможны следующие моменты:

- условие выполнено для одной клетки. Тогда с нее начинаем заполнение таблицы;

- условие выполнено для нескольких клеток. Тогда заполняется та, которой в противоположном ряду соответствует большая разность. Если противоположные разности равны, то заполняем обе клетки;

- условие не выполняется ни для одной клетки. Тогдав строках (столбцах) с наибольшей разностьюотыскивают наименьшую стоимость, из которой вычитают наименьшую стоимость противоположного ряда. В результате получают несколько положительных чисел. Заполняется клетка для которой это число будет наименьшим, после чего разности рассчитывают заново. Если числа будут одинаковыми, то заполняют любую клетку.

Условия оптимальности ТЗ (м/д потенциалов)

Для того чтобы проверить является ли данный опорный план оптимальным, необходимо применить метод потенциалов. Предварительно сделаем необходимые обозначения:

Vj - потенциалы столбцов;

Ui - потенциалы строк;

Cij - стоимость перевозки единицы груза от каждого поставщика каждому потребителю;

Хij - количество груза, которое будет перевезено от i-ro поставщика к j-му потребителю, где i =l,...,m(m-число строк), a j = 1, ...,n (n - число столбцов).

Опорный план транспортной задачи может иметь (m + n -1) отличных от нуля неизвестных. В этом случае план является невырожденным.

Если отличных от нуля неизвестных меньше, чем (m+ n -1), то такой план - вырожденный. И для нахождения оптимального плана одна из пустых клеток таблицы, в этом случае, считается заполненной нулевым грузом.

Опорный план является оптимальным, если выполняются следующие условия:

1. Для заполненных клеток (Xij > 0)

Vi - Ui = Cij

2/ Для пустых клеток (Xij= 0)

Vi - Ui Cij

для всех i= 1, ...,m и j= 1, ...,n.

Для всех пустых клеток, где нарушено второе условие оптимальности, находим характеристику по следующей формуле: Vj-Ui-Cij

Из характеристик выбираем наибольшую и, начиная с клетки с данной характеристикой, строим цепь (цикл) — ломаная линия, вершины которой расположены в занятых клетках таблицы, кроме первой. Повороты цепи! делают под прямым углом. В строке или столбце, где проходит цепь, содержится только две клетки цепи, цепь должна быть замкнута. Клетки цепи отмечаем чередующимися знаками (+) и (-), начиная со знака (+) в первой клетке цепи. Из всех объемов поставок, стоящих в клетках со знаком (-), выбираем минимальный, он обозначается буквой Q. Вычитаем Q из поставок отрицательной полу цепи и прибавляем к поставкам положительной полу цепи.

Пересчитанные грузы записываем в таблицу и пересчитываем потенциалы.

Анализ планово-экономических задач с помощью к-та и оценок симплексных таблиц

Коэф-ты при свободных переменных в 1-вой симпл табл-це наз-ся технико-экономическими коэф-ми и показ-ют какие изменения произойдут в базисе при введении в него ед-цы размерности этой своб переменной. Сущ опред-ные правила введения в базис единицы размерности соотв переменной.

Правило 1. Если в базис вводится ед-ца размерности основной свобод переменной, то чтобы н-ти нов знач-я базис перем-х нужно из своб членов вычесть соотв коэф-ты столбца этой переменной с учетом знака.

Правило 2. Если в базис вводится ед-ца размерности дополнит свободной переменной, то чтобы н-ти нов знач-я бази-х переем-х нужно к своб членам прибавить соотв-щие к-ты столбца этой переменной с учетом знака.

К-ты бывшей разреш строки наз-ся к-тами взаимозаменяемости с (.) зрения диф-та ресурса.

Св-ва ДО: 1-ое связано с мерой дефицитности рес-сов. Если огр-е выпол-ся как строгое рав-во, то оц-ка б. ненулевая,если как нерав-во – то нулевая. Чем дефицитней рес-с, тем выше оц-ка. Исполь-е данного св-ва ДО позволяет вскрыть узкие места сдерж-щие рост произ-ва. Помогает выбрать правильное реш-е, если предполаг-ся расш-е произ-ва и треб-ся привл-е допол-х рес-в.

2. устойчивость оц-ки опт-ого пл. ДО уст-вы к изм-ю объемов произ-ых рес-ов, т.е. они не меняют своей вел-ны при изм-ии объемов произ-ых рес-ов довольно широких диапозонах изм-я, но они очень чувствительны к изм-ям вел-н коэф. цел. функ. и технико-экон. коэф.

3. связано с мерой влияния огран-я на функционал. ДО имеют ту же ед-цу измерения что и функционал. Ненул. оц показ-т как изм-ся вел-на функционала при введении в план ед-цы размерности св.п. По рес-сам (допол. перем): при увел. на ед-цу размерности функционал увел. на вел-ну оц. По продуктам (осн. перем): при увел. на ед-цу размерности данного продукта функционал умень на вел-ну оц-ки. Нулев. оц по рес-сам (продуктам) свид-т о том, что изм-я объема огран-я на ед-цу не повлияет на знач. функционала, т.к. рес-с по опт-му плану в избытке или продукт произведен сверх плана.

4.ДО- мера взаимозаменяемости рес-ов (продуктов), но не абсолютной, а относительной с точки зрения цел.функции

5. ДО- мера рент-ти отдель. спос-ов произ-ва. Те сп-бы, кот. вошли в опт-й пл рент-ны и суммарная оц. произ-ых рес-ов, затраченных по этому сп-бу будет равна той прибыли, кот. от него можно получить. Огр-я ДЗ будут выражены как строгие рав-ва. Для не рент-ых сп-ов суммарная оц-ка произ-ых рес-ов будет больше той прибыли, кот. дает этот СП-б, т.е. соот-щие огр-я ДЗ будет вып-но как строгое нер-во типа >.

Корректировка оптимального плана

Правило 1. Если в базис вводится основная переменная, то наибольшее значение которое она может принять определяется наименьшим отношением свободных членов к +-м коэффициентам столбца этой переменной. Правило 2. Если в план вводится дополнительная переменная, то наибольшее значение которое она может принять определяется наименьшим отношением свободных членов к отрицательным коэффициентам столбца этой переменной, взятых по абсолютной величине.

Экон. интепретация ДЗ. ДО опт-ого плана.

Левая часть ограничений ДЗ определяет суммарную денеж оц-ку всех производст ресурсов, затрач-х на 1 га посевов сотв культуры. Эта суммарн оц-ка дб не < той ст-ти валов прод-ции, кот-ю получ-т с 1 га соотв культуры. Целевой функц-ей ДЗ служит суммар оц-ка всех производст ресур-в, выдел на воздес всех культур. И эта оц-ка дб мин-ной.

Из теор двойст-ти следует, что Zmax=Wmin, те миним оц-ка всех производ ресур дб = той ст-ти валов прод-ции, кот м/получ при воздел этих культур.

Прямые зад.- зад., кот. обесп-т расчет опт-ого пл, а ДЗ – опт-х оц-к произ-ых рес-ов, кот. еще наз-т ДО.

4.ДО- мера взаимозаменяемости рес-ов (продуктов), но не абсолютной, а относительной с точки зрения цел.функции

17. Базовая структурная ЭММ задач, решаемых симплекснам м/дом

Базовая структурная ЭММ задач, решаемых симплекс-методом, имеет вид:

Целевая функция достигает экстремума

Z _max₍_min₎=S C_jX_j ,

^j⁼¹

при условии выполнения трех ограничений:

1)по использованию производственных ресурсов - затраты i -ого ресурса на производство j - ой продукции не будут превышать наличного объема этого ресурса;

S a_ijx_j£ b_i iÎI₁

^j=1

где

Xj-основная переменная, a_ij- норма затрат производственного ресурса i -го вида на единицу размерности j – ой, b_i- объем ресурса

2) по заданному объему выполнения работ или производства продукции - объем производства продукции i -ого вида в расчете на единицу j-ой переменной будет не меньше гарантированного объема;

S v_ijx_j ³ Q_iiÎI₂,

^j⁼¹

где

v_ij - выход продукцииi-го вида с единицы размерности j-ой переменной ( урожайность , продуктивность) .

Q_i - гарантированный объем производства i -ого вида продукции .

3) условие неотрицательности переменных - поскольку искомые величины являются реальными положительными величинами (посевная площадь, поголовье, объем кормов и т.д.)

X_j ³0 j=1,...,n,

18. Базовая структурная ЭММ задач, решаемых распределительным м/дом

аi – кол-во груза у i пост-ка, bj – потреб-сть в этом грузе j потребителя, Сij – ст-ть (с/с) перевозки ед-цы груза от i пост-ка к j потреб-лю, Xij – кол-во груза, перевозимое от i пост-ка к j потр-лю.

Найти значение переменных Хij, где i=1-m, j=1-n, обеспеч-щих целевой ф-ции Z= m _n

S ∑Cij*Xij→миним и удовлетвор след

ⁱ⁼¹^j⁼¹

сис-ме ограничений: 1) Сумма всех грузов, перевозимых от i пост-ка дб = запасу груза у этого пост-ка

S x_jj= a_i, i=1-m.

^j⁼¹

2) Сумма всех грузов, доствляемых j потребителю д/равняться потребности этого потребителя:

S x_jj= bj, j=1-n.

ⁱ⁼¹

3) Условие неотриц-ти переменных: Хij>=0, j=1-n, i=1-m.

Если

m _n

Sa_i=∑bj, модель закрыта. Если не= , то

ⁱ⁼¹^j⁼¹модель я/я открытой.

Чтобы сдела модель закрытой, необх ввести фиктивного пост-ка, если потребность > запаса или фиктивного потребителя, если запас > потребности. Целевая ф-ция обыч берется на минимум ст-ти перевозки груза или мин времени, затрач на перевозку груза.

Производственные функции

Сельскохозяйственное производство характеризуется системой экономических показателей, отражающих как условия производства, так и его результаты. Эти показатели, как правило, связаны между собой. Изучение характера этих взаимосвязей имеет важное значение в планировании и управлении производством (например, зависимость производительности труда от квалификации работников, урожайности от доз удобрений и качества почв, продуктивности животных от уровня кормления и условий содержания и т.п.). Особенно важным является исследование связи между результативными показателями и определяющими их факторами производства.

Различают две формы связи между признаками: функциональную и корреляционную.

Связь называется функц., если изменения факторногопризнака х (аргумента) приводят к строго опред. измен. результативного признака у (функции): у=f(х].

Корреляционной называется такая форма связи между призн., когда изменение факт. признака на одну и ту же величину сопровожд. неодинак. изм. результат. призн. В общем виде ур. можно записать так: у_Х = а + bх, где у_х — значение рез-го призн, опред-ое в сред под влиянием данного Ур. фактора х;

Ь — коэфф. пропорц-ти (регрессии). Он показ. ср. прибавку рез-го признака при изменении факт. на ед;

а — начало отсчета; Мат. соотношение, показ-ее связь м-у факт. и рез. призн, наз. уравнением регрессии.

Простые уравнения регрессии характеризуют зависимость результативного признака от 1го фактора. Многофакторные уравнения регрессии описывают зав. рез-го призн. от неско. факторов:

У=а₀+а₁х₁+а₂х₂+…+ а_пх_п.

В эк. особое зн. имеет исслед. хар-ра влияния факторов производства на его конечные результаты, и прежде всего на выход продукции. В связи с этим сформировалось самост. направление эк. исследований под названием теории производственных функций Задачей их явл. выяснение колич. хар-к связи м-у затр. произ-ых рес-в и вып. прод. Исследование произв. функций основано на использовании мат. аппарата корреляционного анализа.

Приемы моделирования

1)Методы изменения свободных членов при неизменных коэффициентов переменных величин.1) Установление определенных границ для свободного члена, когда эти границы известны:

bi^/<=bi<=bi^//, ∑аij*хj<=bi

j€J

1 – использ-е трудовых ресурсов по минимуму: ∑ аij*хj>=bi^/

j€J

2 – использ-е труд ресурсов по макси-му:

∑ аij*хj<=bi^//

j€J

2) Когда границы свободного члена неизвестны и его величина будет зависеть от условий или факторов и определяется в процессе решения задачи. В этом случае в систему ограничений вводится дополнительная переменная xj, кот обознач пополнение ресурса.

∑aίjxj ≤ вί+xj, ∑aίjxj־xj ≤вί j€z j€z

2) Приемы моделирования, приёмы запи-си ограничений с измен-ся коэффи-циентами при переменных.

1) Метод средней взвешенной. Известно, что коэффициенты при переменной: aίj′ ≤aίj ≤aίj″ , νίj′ ≤νίj ≤νίj″, xj′ ≤xj ≤xj″.

1. xj′>0, xj″=0, xj=xj′, aίj′=aίj, νίj′=νίj.

2. xj′=0, xj″=0, xj=xj″, aίj=aίj″, νίj=νίj″.

3. xj′>0, xj″>0, aίj^ист=(aίj′*xj′+aίj″*xj″) / (x′+x″), νίj ^ист=(νίj′*xj′+νίj″*xίj″) / (xj′+xj″).

2) Метод суммирования коэффициентов. Этот прием м.б. использован для отражения процесса интенсификации, когда увеличение выхода продукции с ед. площади идет за счет дополнительных затрат. Этот прием используется при оптимизации кормовой базы, при балансировании годовых рационов кормления животных. Пусть xj - размерность некоторой отрасли, aίj- нормы затрат ί-го производственного ресурса на ед. размерности j-й отрасли; νίj- выход продукции ί-го вида, на ед. размерности j-й переменной.

Ограничения. 1. по общему объему произведенной продукции i- го вида, по j- й отрасли: νίj*xj+xj=x_к. 2. по приросту продукции: xj≤(νίj′-νίj)*xj, xj-νίj′+νίjxj≤0. 3. баланс производственных ресурсов: aίjxj+dίjxj≤вί, dίj- добавочные затраты, dίj=aίj′-aίj ⁄ νίj′-νίj. После решения задачи исчисляются истинные значения коэффициентов: ист. νίj=νίj+xj:xj, ист. aίj=aίj+dίj*xj:xj.