Прынцыпыпабудовы ЭВМ. Фон нейман

Третий этап

Третий этап (до 1970 г.). Увеличения быстродействия и надежности полупроводниковых схем, а также уменьшения их габаритов, потребляемой мощности и стоимости удалось добиться за счет создания технологии производства интегральных микросхем (ИС), состоящих из десятков электронных элементов, образованных в прямоугольной пластине кремния с длиной стороны не более 1 см. Такая пластина (кристалл) размещается в небольшом пластмассовом корпусе, размеры которого, как правило, определяются только числом “ножек” (выводов от входов и выходов электронной схемы, созданной на кристалле). Это позволило не только повысить производительность и снизить стоимость универсальных ЭВМ (больших ЭВМ), но и создать малогабаритные, простые, дешевые и надежные машины — мини-ЭВМ. Мини-ЭВМ первоначально предназначались для замены аппаратно-реализованных контроллеров (устройств управления) в контуре управления каким-либо объектом, в автоматизированных системах управления технологическими процессами, системах сбора и обработки экспериментальных данных, различных управляющих комплексах на подвижных объектах и т. д. Появление мини-ЭВМ позволило сократить сроки разработки контроллеров. Вместо длительной процедуры разработки и создания сложной электронной схемы надо было лишь купить готовый универсальный “полуфабрикат” контроллера, чтобы потом запрограммировать его на выполнение требуемых функций. Правда, такое универсальное устройство, как правило, обладало функциональной избыточностью (для создаваемого контроллера могли не потребоваться некоторые команды мини-ЭВМ, часть ее памяти, высокое быстродействие и т. п.). Однако низкая цена серийной мини-ЭВМ, большое число серийных устройств связи с объектом управления и хорошее программное обеспечение обычно обусловливали экономическую эффективность использования такого программируемого контроллера. Организации, покупавшие мини-ЭВМ для создания контроллеров, довольно быстро поняли, что на этих машинах можно решать и вычислительные задачи традиционные задачи больших ЭВМ. Простота обслуживания мини-ЭВМ, их сравнительно низкая стоимость и малые габариты позволяли снабдить этими машинами небольшие коллективы исследователей, разработчиков, экспериментаторов и обучающихся, т. е. дать их прямо в руки пользователей ЭВМ. В начале 70-х годов с термином мини-ЭВМ связывали уже два существенно различных типа средств вычислительной техники: универсальный блок обработки данных и выдачи управляющих сигналов, серийно выпускаемый для применения в различных специализированных системах контроля и управления; небольших габаритов универсальную ЭВМ, проблемно-ориентированную пользователем на решение ограниченного круга задач в рамках одной лаборатории, технологического участка, т. е. задач, в решении которых оказывались заинтересованными 10—20 человек, работавших над одной проблемой.

Четвёртый этап

 

етвертый этап (до 1978 г.). Успехи в развитии электроники привели к созданию больших интегральных схем (БИС), где в одном кристалле размещалось несколько десятков тысяч электрических элементов. Это позволило разработать более дешевые ЭВМ, имеющие большую память и меньший цикл выполнения команды: стоимость байта памяти и одной машинной операции начала резко снижаться. Но так как затраты на программирование почти не сокращались, то на первый план вышла задача экономии человеческих, а не машинных ресурсов. Разрабатывались новые операционные системы, позволяющие программистам отлаживать свои программы прямо за дисплеем ЭВМ (в диалоговом режиме), что облегчало работу пользователей ЭВМ и ускоряло разработку программ. Это полностью противоречило концепциям первых этапов информационной технологии: “процессор выполняет лишь ту часть работы по обработке данных, которую люди принципиально выполнить не могут,— массовый счет”. Стала прослеживаться другая тенденция: “все, что могут делать машины, должны делать машины; люди выполняют лишь ту часть работы, которую нельзя автоматизировать”. В 1971 г. была изготовлена первая БИС, в которой полностью размещался процессор ЭВМ простой архитектуры. Стала реальной возможность размещения в одной БИС (на одном кристалле) почти всех электронных устройств несложных по архитектуре ЭВМ, т. е. возможность серийного выпуска простых ЭВМ стоимостью 5—50 руб. (без учета стоимости внешних устройств). Появились дешевые . (карманные клавишные ЭВМ) и — управляющие устройства, построенные на одной или нескольких БИС, содержащих процессор, память и системы связи с датчиками и исполнительными органами в объекте управления (т. е. с внешними устройствами такой специализированной ЭВМ). Программы управления подачей топлива в двигатель автомобиля, движением электронной игрушки или заданным режимом стирки белья вводились в память ЭВМ либо при изготовлении подобного контроллера, либо непосредственно на предприятиях, выпускающих автомобили, игрушки, стиральные машины и т. п. В 70-х годах стали изготавливать и универсальные вычислительные системы, состоящие из процессора, памяти, схем сопряжения с устройствами ввода-вывода и тактового генератора, размещенных в одной БИС (однокристальная ЭВМ) или в нескольких БИС, установленных на одной печатной плате (одноплатная ЭВМ). Таким образом, повторялась картина 60-х годов, когда первые мини-ЭВМ отбирали часть работы у больших универсальных ЭВМ.

Пятый этап

Пятый этап. Улучшение технологии производства БИС позволяло изготавливать дешевые электронные схемы, содержащие сотни тысяч элементов в кристалле—схемы сверхбольшой степени интеграции (СБИС). Появилась возможность создать настольный прибор с габаритами массового телевизора, в котором размещались микроЭВМ, клавиатура, экран, кассетный магнитофон (или гибкий диск), а также схемы сопряжения с малогабаритным печатающим устройством (например, с электрической пишущей машинкой), измерительной аппаратурой, другими ЭВМ и т. д. Благодаря операционной системе, обеспечивающей простоту общения с этой ЭВМ, большой библиотеке прикладных программ по различным отраслям человеческой деятельности, а такжемалой стоимости такой персоне то, становится необходимой принадлежностью инженера, исследователя, экономиста, врача, агронома, преподавателя, редактора, секретаря и даже ребенка. Кроме функций помощника в решении традиционных задач расчетного характера персональный компьютер (ПК) может выполнять работу личного секретаря: помогать в составлении личной картотеки и ведении рабочей тетради; создавать, хранить (например, на магнитной ленте), редактировать и размножать различные тексты (письма, документы, статьи, конспекты лекций и даже книги); получать по линиям связи различные справочные данные из библиотек и архивов и т. д. ПК можно использовать для обучения детей (с помощью учебных машинных курсов), в развлекательных целях (от остросюжетных до познавательных игр) и во многих других приложениях. Наиболее широкое применение нашли микроЭВМ в гибких системах автоматизации производства (ГАП) и научных исследований (АСНИ). Здесь используются как персональные компьютеры, так и встраиваемые в аппаратуру микроконтроллеры и микроЭВМ. Существует и множество других приложений микроЭВМ. Для построения интеллектуальных систем и устройств выпускается очень большое число вычислительных средств: общий объем мирового производства оценивался в 1985 г. на уровне 200 млн микропроцессоров и 10 млн персональных компьютеров в год. Их встраивание в аппаратуру, обслуживание и программирование требует колоссального числа специалистов, которых нельзя (да и нецелесообразно) готовить в рамках одной специальности. Поэтому программирование постепенно перекладывается на плечи непрофессиональных программистов — специалистов различных отраслей народного хозяйства, которые приобрели начальные навыки программирования, освоив небольшие по объему дисциплины в техникумах, вузах или на курсах повышения квалификации. Эти же непрофессионалы должны выполнять и часть работ по встраиванию микроЭВМ в разрабатываемую ими аппаратуру. В связи с этим сейчас так много людей изучает в том или ином объеме устройство микроЭВМ и их язык.

 

Прынцыпыпабудовы ЭВМ. Фон нейман

он Нейман был широко известен как выдающийся математик, и научная общественность приписала ему все идеи, лежащие в основе этой машины. В обиход вошло выражение “машина фон Неймана» (т.е. компьютер). Нейман нашел путь подключения рабочей программы не проводами или другими соединениями, а интегрированием ее в память машины в закодированном виде. Именно Нейман и придумал схему, которой до сих пор следуют все цифровые компьютеры. В общем виде схема представлена на рисунке. Сплошные стрелки — это управляющие связи (по ним идут сигналы управления), а пунктирные стрелки — это информационные связи (по ним идут данные, информация). К устройствам ввода/вывода относятся клавиатура, мышь, монитор, дисковод, CD ROM, принтер, сканер, микрофон, звуковые колонки, плоттер и т.д.

 

Компьютер должен иметь:

арифметическо-логическое устройство, выполняющее арифметические и логические операции. В наше время это устройство называется центральный процессор. Центральный процессор (centralprocessingunit) – микропроцессор компьютера, представляющий собой микросхему, которая управляет всеми процессами, происходящими в компьютере;

устройство управления, которое организует процесс выполнения программ. В современных компьютерах арифметическо-логическое устройство и устройство управления объединены в центральный процессор;

запоминающее устройство (память) для хранения программ и данных;

внешние устройства для ввода-вывода информации.

 

Память компьютера представляет собой некоторое количество пронумерованных ячеек, в каждой из которых могут находиться или обрабатываемые данные, или инструкции программ. Все ячейки памяти должны быть одинаково легко доступны для других устройств компьютера.

 

Принцип работы:

С помощью внешнего устройства в память компьютера вводится программа.

Устройство управления считывает содержимое ячейки памяти, где находится первая инструкция (команда) программы и организует ее выполнение. Команда может задавать:

выполнение логических или арифметических операций;

чтение из памяти данных для выполнения арифметических или логических операций;

запись результатов в память;

ввод данных из внешнего устройства в память;

вывод данных из памяти на внешнее устройство.

Устройство управления начинает выполнение команды из ячейки памяти, которая находится непосредственно за только что выполненной командой. Однако этот порядок может быть изменен с помощью команд передачи управления (перехода). Эти команды указывают устройству управления, что ему необходимо продолжить выполнение программы, начиная с команды, содержащейся в иной ячейки памяти.

Результаты выполнения программы выводятся на внешнее устройство компьютера.

Компьютер переходит в режим ожидания сигнала от внешнего устройства.

 

Один из принципов "Архитектуры фон Неймана" гласит: в компьютере не придется изменять подключения проводов, если все инструкции будут храниться в его памяти . И как только эту идею в рамках “архитектуры фон Неймана» воплотили на практике, родился современный компьютер.

 

Аналоговые ЭВМ

Аналоговая вычислительная машина (АВМ), вычислительная машина, в которой каждому мгновенному значению переменной величины, участвующей в исходных соотношениях, ставится в соответствие мгновенное значение другой (машинной) величины, часто отличающейся от исходной физической природой и масштабным коэффициентом. Каждой элементарной математической операции над машинными величинами, как правило, соответствует некоторый физический закон, устанавливающий математические зависимости между физическими величинами на выходе и входе решающего элемента (например, законы Ома и Кирхгофа для электрических цепей, выражение для эффекта Холла, лоренцовой силы и т. д.).

 

Особенности представления исходных величин и построения отдельных решающих элементов в значительной мере предопределяют сравнительно большую скорость работы АВМ, простоту программирования и набора задач, ограничивая, однако, область применения и точность получаемого результата. АВМ отличается также малой универсальностью (алгоритмическая ограниченность) — при переходе от решения задач одного класса к другому требуется изменять структуру машины и число решающих элементов.

АВМ в основном применяется при решении следующих задач. Контроль и управление. В системах автоматического управления АВМ пользуются, как правило, для определения или формирования закона управления, для вычисления сводных параметров процесса (кпд, мощность, производительность и др.). Если задано математическое выражение, определяющее связь сводного параметра или управляющего воздействия с координатами объекта, АВМ служат для решения соответствующего уравнения. Результат вычислений поступает либо на исполнительный механизм (замкнутая система), либо к оператору. В последнем случае АВМ работает как информационное устройство. Например, АВМ широко распространены для оценки экономической эффективности энергетических систем, и те же АВМ могут управлять исполнительными механизмами, т. е. служить автоматическими регуляторами. Когда закон управления заранее не определён, а заданы лишь некоторый критерий оптимальности и граничные условия, АВМ применяются в системах поиска оптимального управления и служат математическ. моделью объекта.

АВМ состоят из некоторого числа решающих элементов, которые по характеру выполняемых математических операций делятся на линейные, нелинейные и логические. Линейные решающие элементы выполняют операции суммирования, интегрирования, перемены знака, умножения на постоянную величину и др. Нелинейные (функциональные преобразователи) воспроизводят нелинейные зависимости. Различают решающие элементы, предназначенные для воспроизведения заданной функции от одного, двух и большего числа аргументов. Из этого класса обычно выделяют устройства для воспроизведения разрывных функций одного аргумента (типичные нелинейности) и множительно-делительные устройства (см. Перемножающее устройство). К логическим решающим элементам относятся устройства непрерывной логики, например предназначенные для выделения наибольшей или наименьшей из нескольких величин, а также устройства дискретной логики, релейные переключающие схемы и некоторые др. специальные блоки. Для связи устройств непрерывной и дискретной логики широко пользуются гибридными логическими устройствами (например, компараторами). Все логические устройства обычно объединяются в одном, получившем название устройства параллельной логики. Оно снабжается своим наборным полем для соединения отдельных логических устройств между собой и с остальными решающими элементами АВМ.

Особенности: Их нельзя программировать, как ЦВМ, они работают по жесткой схеме. Впрочем, нет, можно ими управлять с помощью переключателей между аналоговыми элемнтами, но цифровые переключатели вносят дополнительную погрешность, а механические дороги, медлительны и ненадежны.

Прадстауленне непрырыунай инфармацыи

Под информацией в широком смысле принято понимать различные сведения о событиях в общественной жизни, явлениях природы, о процессах в технических устройствах. Она содержатся в нашей речи, в текстах книг и газет, в показаниях измерительных приборов и отображает разнообразие, присущее объектам и явлениям реального мира. Информацию, воплощенную и зафиксированную а некоторой материальной форме, называют сообщением и передают с помощью сигналов. Природа большинства физических величин такова, что они могут принимать любые значения в каком-то диапазоне (температура, давление, скорость и т.д.). Сигнал, отображающий эту информацию и возникающий на выходе соответствующего датчика, на любом временном интервале может иметь бесконечное число значений. Так как в данном случае непрерывный сигнал изменяется аналогично исходной информации, его обычно называют аналоговым, а устройства, в которых действуют такие сигналы – аналоговыми. Существуют также дискретные сообщения, параметры которых содержат фиксированный набор отдельных значений. А так как этот набор конечен, то и объем информации в таких сообщениях конечен.

 

На практике непрерывные сообщения можно представлять в дискретной форме. Непрерывность сообщений по величине не может быть реализована в связи с погрешностью источников и приемников информации и наличием помех в канале передали информации. Поэтому к непрерывным сигналам, отображающим сообщения, можно применять квантование по уровню и по времени, При квантовании по уровню совокупность возможных значений напряжения или тока заменяют конечным набором дискретных значений из этого из этого интервала. Квантование по времени предусматривает замену непрерывного сигнала последовательностью импульсов, следующих через определенные промежутки временя (рис. 1), называемых тактовыми. Если тактовые интервалы выбраны соответствующим образом, то потери информации не происходит. При одновременном введении квантования по времени и по уровню амплитуда каждой выборки будет принимать ближайшее разрешенное значение из выбранного конечного набора значений. Совокупность всех выборок образует дискретный или цифровой сигнал. Каждое значение дискретного сигнала можно представить числом. В цифровой технике такой процесс называется кодированием (дискретизацией), а совокупность полученных чисел—кодом сигнала.

++Дискретизация.Запись на грампластинке — хороший пример сохранения информации о времени и амплитуде. Размах модуляции звуковой канавки кодирует значение амплитуды звукового сигнала; чем больше эта модуляция, тем больше амплитуда сигнала. Временная информация кодируется благодаря вращению грампластинки с одинаковой угловой скоростью как при записи, так и при воспроизведении. Если мы изменим скорость вращения проигрывателя, то изменятся временные соотношения и, следовательно, частота сигнала.

 

В цифровом сигнале также должна сохраняться временная и амплитудная информация исходного звука. Но вместо кодирования и записи этих параметров в аналоговой форме (как на грампластинке), в цифровой записи временные и амплитудные параметры сохранены в дискретной форме.

 

Временная информация кодируется в цифровой аудиосистеме путем периодического измерения мгновенных значений аудиосигнала. Дискретное значение аналогового сигнала называют отсчетом. Амплитудная информация кодируется в результате представления значения каждого отсчета при помощи числа. Этот процесс называется квантованием. Таким образом, дискретизация по времени и квантование по уровню являются основой цифровой звукотехники: дискретизация сохраняет временную информацию, квантование — амплитудную.

В результате выполнения дискретизации по времени и квантования по уровню возникает последовательность двоичных чисел, называемых словами, которые представляют форму аналогового сигнала. Если преобразовать эти двоичные слова обратно в напряжение с сохранением исходных параметров первоначальной дискретизации по времени, то приблизительно будет воссоздана форма аналогового звукового сигнала. Для более точного восстановления исходной формы звукового сигнала необходимо дополнительно сгладить импульсы напряжения прямоугольной формы при помощи фильтра нижних частот. Таким образом дискретизация по времени и квантование по уровню преобразуют непрерывную аналоговую функцию (непрерывно изменяющееся напряжение аналогового сигнала) в последовательность дискретных двоичных чисел. На рис. В-2 показано, как непрерывный аналоговый сигнал преобразуется в двоичные числа и обратно в непрерывный аналоговый сигнал.

 

Правило выбора предельного шага при равномерной дискретизации с использованием модели сигнала с ограниченным спектром сформулировано академиком В. А. Котельниковым: «Любая непрерывная функция s(t), спектр которой ограничен частотой Fmax полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга на интервал 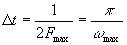» Кроме того, теорема Котельникова дает и способ точного восстановления сигнала 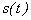по его отсчетам.

Доказательство

 

Мадуляция

Под модуляцией понимается процесс преобразования информационного сигнала в сигнал, предназначенный для передачи по линии. В простейшем случае для модуляции сигнала используется специальный высокочастотный сигнал определённой частоты, которая называется несущей. Процесс обратного преобразования модулированного сигнала называется демодуляцией.

Кодирование информации

При передаче информации происходит кодирование информации, и мы должны договориться о том, как понимать те или иные обозначения.

Человек выражает свои мысли словами. Они являются алфавитным представлением информации. На уроках физики при рассмотрении какого-либо явления мы используем формулы. В этом случае говорят о языке алгебры. Формула - это математический код. Существует язык глухонемых, где символы - мимика и жесты; язык музыки, где символы - ноты и т.д.

Основу любого языка составляет алфавит - конечный набор различных символов, из кото-рых складывается сообщение.

Одна и та же запись может нести разную смысловую нагрузку. Например, набор цифр 251299 может обозначать: массу объекта; длину объекта; расстояние между объектами; номер телефона; дату 25 декабря 1999 года. Эти примеры говорят, что для представления информации могут использоваться разные коды, и поэтому надо знать законы записи этих кодов, т.е. уметь кодировать.

Код - набор условных обозначений для представления информации. Кодирование - процесс представления информации в виде кода. Кодирование сводится к использованию совокупности символов по строго определенным правилам. При переходе улицы мы встречаемся с кодированием информации в виде сигналов светофора. Водитель передает сигнал с помощью гудка или миганием фар. Кодировать инфор-мацию можно устно, письменно, жестами или сигналами любой другой природы. По мере разви-тия техники появились разные способы кодирования информации. Во второй половине XIX века американский изобретатель Морзе изобрел удивительный код, который служит человечеству до сих пор.

 

В качестве источников информации может выступать человек, техническое устройство, предметы, объекты живой и неживой природы. Получателей сообщения может быть несколько или один.

В процессе обмена информацией мы совершаем две операции: кодирование и декодирование. При кодировании происходит переход от исходной формы представления информации в форму, удобную для хранения, передачи или обработки, а при декодировании - в обратном направлении.

 

Кодирование информации в двоичном коде

 

Существуют разные способы кодирования и декодирования информации в компьютере. Это зависит от вида информации: текст, число, графическое изображение или звук. Для числа также важно, как оно будет использовано: в тексте, или в вычислениях, или в процессе ввода-вывода. Вся информация кодируется в двоичной системе счисления: с помощью цифр 0 и 1. Эти два символа называют двоичными цифрами или битами. Такой способ кодирования технически просто организовать: 1 - есть электрический сигнал, 0 - нет сигнала. Недостаток двоичного кодирования - длинные коды. Но в технике легче иметь дело с большим числом простых однотип-ных элементов, чем с небольшим числом сложных.

 

Кодирование текстовой информации

 

При нажатии клавиши клавиатуры сигнал посылается в компьютер в виде двоичногочис-ла, которое хранится в кодовой таблице. Кодовая таблица - это внутреннее представление символов в компьютере. В качестве стандарта в мире принята таблица ASCII (AmericanStandartCodeforInformationInterchange - Американский стандартный код для обмена информацией). Для хранения двоичного кода одного символа выделен 1 байт = 8бит. Так как 1 бит принимает значение 0 или 1, то с помощью одного байта можно закодировать 28 = 256 различных символов, т.к. именно столько различных кодовых комбинаций можно составить. Эти комбинации и со-ставляют таблицу ASCII. Например, буква S имеет код 01010011; при нажатии ее на клавиатуре происходит декодирование двоичного кода и по нему строится изображение символа на экране монитора.

 

Стандарт ASCII определяет первые 128 символов: цифры, буквы латинского алфавита, управляющие символы. Вторая половина кодовой таблицы не определена американским стандартом и предназначена для национальных символов, псевдографических и некоторых немате-матических символов. В разных странах могут использоваться различные варианты второй половины кодовой таблицы. Цифры кодируются по этому стандарту при вводе-выводе и если они встречаются в тексте. Если они участвуют в вычислениях, то осуществляется их преобразование в другой двоичный код.

 

Кодирование чисел.

 

В двоичной системе счисления для представления используются две цифры 0 и 1.

Сравните:

в десятичной системе счисления 435,6710 = 4 102 + 3 101 + 5 100 + 6 10-1 + 7 10-2 в десятичной системе счисления 10110,1012 = 1 24 +0 23 +1 22 +1 21 +0 20 +1 2-1 +0 2-2 +1 2-3

Действия с числами в двоичной системе счисления изучает наука двоичная арифметика. Все основные законы арифметических действий для таких чисел также выполняются.

Для сравнения рассмотрим два варианта кодирования для числа 45. При использовании числа в тексте каждая цифра кодируется 8 битами в соответствии с ASCII (т.е. потребуется 2 байта): 4 - 01000011, 5 - 01010011. При использовании в вычислениях код этого числа получается по специальным правилам перевода из десятичной системы счисления в двоичную в виде 8-разрядного двоичного числа: 4510 = 001011012, что потребует 1 байт.

 

Кодирование графической информации

 

Графический объект в компьютере может быть представлен как растровое или векторное изображение. От этого зависит и способ кодирования. Растровое изображение представляет собой совокупность точек различного цвета. Объем растрового изображения равен произведению количества точек на информационный объем одной точки, который зависит от количества возможных цветов. Для черно-белого изображения информационный объем точки равен 1 биту, т.к. она может быть либо белой, либо черной, что можно закодировать двумя цифрами 0 и 1. Рассмотрим, сколько потребуется бит для изображе-ния точки: 8 цветов - 3 бита (8 = 23); для 16 цветов - 4 бита (16 = 24); для 256 цветов - 8 битов (1 байт). Различные цвета получаются из трех основных - красного, зеленого и синего. Векторное изображение представляет собой графический объект, состоящий из элементарных отрезков и дуг. Положение этих элементарных объектов определяется координатами точек и длиной радиуса. Для каждой линии указывается ее тип (сплошная, пунктирная, штрих-пунктирная), толщина и цвет. Информация о векторном изображении кодируется как обычная буквенно-цифровая и обрабатывается специальными программами.

 

Памехаустойливае кадзираванне. Код Грея, Хеминга

Целью помехоустойчивого кодирования является повышение достоверности доставки сообщений, передаваемых по каналам связи с помехами.

 

 

Паняцце ифнармацыы

Информация (от лат. informatio — осведомление, разъяснение, изложение, от лат. informare — придавать форму) — в широком смысле абстрактное понятие, имеющее множество значений, в зависимости от контекста.

В информатике нет строгого определения информации, но можно установить условие существования информации в сигнале — сигнал содержит информацию, если значение этого сигнала (заведомо) неопределенно для получателя.

 

Информация всегда связана с материальным носителем, с материальными процессами и имеет некоторое представление. Информация, представленная в какой-либо форме, называется сообщением. Сообщения представляются в виде сигналов и данных. Сигналы используются для передачи информации в пространстве между источником и получателем, а данные — для хранения (то есть для передачи во времени).

 

Сигнал — изменяющийся во времени физический процесс, изменение параметров которого и несёт информацию к получателю.

 

Данные — результат фиксации, отображения информации на каком-либо материальном носителе, в виде состояния (формы) этого носителя. При этом предполагается возможность хотя бы однократное изменение этого состояния.

 

Данные, являющиеся результатом фиксации некоторой информации, сами могут выступать как источник информации. Информация, извлекаемая из данных, может подвергаться обработке, и результаты обработки фиксируются в виде новых данных. Общая схема взаимоотношений между понятиями «информация» и «данные» в информационных системах может выглядеть следующим образом:

 

Предметом изучения науки информатика являются именно данные: методы их создания, хранения, обработки и передачи [2]. А сама информация, зафиксированная в данных, ее содержательный смысл интересны пользователям информационных систем, являющимся специалистами различных наук и областей деятельности: медика интересует медицинская информация, геолога — геологическая, предпринимателя — коммерческая и тп. (в том числе специалиста по информатике интересует информация по вопросам работы с данными).

 

Совокупность данных, представляющих сообщение на материальном носителе, образует документ.

Документ — материальный объект, содержащий информацию в зафиксированном виде и специально предназначенный для её передачи во времени и пространстве.

Информационные технологии (ИТ, от англ. informationtechnology, IT) — это класс областей деятельности, относящихся к технологиям управления и обработкой огромного потока информации с применением вычислительной техники.

Согласно определению, принятому ЮНЕСКО, Информационные Технологии (ИТ) — это комплекс взаимосвязанных научных, технологических, инженерных наук, изучающих методы эффективной организации труда людей, занятых обработкой и хранением информации с помощью вычислительной техники и методы организации и взаимодействия с людьми и производственным оборудованием, их практические применение, а также связанные со всем этим социальные, экономические и культурные проблемы. Основные черты современных ИТ:

-компьютерная обработка информации;

-хранение больших объёмов информации на машинных носителях;

-передача информации на любые расстояния в кротчайшие сроки.

Современное материальное производство и другие сферы деятельности все больше нуждаются в информационном обслуживании, переработке огромного количества информации. Универсальным техническим средством обработки любой информации является компьютер, который играет роль усилителя интеллектуальных возможностей человека и общества в целом, а коммуникационные средства, использующие компьютеры, служат для связи и передачи информации. Появление и развитие компьютеров — это необходимая составляющая процесса информатизации общества.

Информатизация на базе внедрения компьютерных и телекоммуникационных технологий является реакцией общества на потребность в существенном увеличении производительности труда в информационном секторе общественного производства, где сосредоточено более половины трудоспособного населения. Так, например, в информационной сфере США занято более 60% трудоспособного населения, в СНГ — около 40%.[1]

Современные информационные технологии

Современные информационные технологии с их стремительно растущим потенциалом и быстро снижающимися издержками открывают большие возможности для новых форм организации труда и занятости в рамках как отдельных корпораций, так и общества в целом. Спектр таких возможностей значительно расширяется - нововведения воздействуют на все сферы жизни людей, семью, образование, работу, географические границы человеческих общностей и т. д. Сегодня информационные технологии могут внести решающий вклад в укрепление взаимосвязи между ростом производительности труда, объемов производства, инвестиций и занятости. Новые виды услуг, распространяющиеся по сетям, в состоянии создать немало рабочих мест, что подтверждает практика последних лет.

До начала 1980-х годов информационные технологии были представлены главным образом большими ЭВМ и использовались для нужд лишь половины корпоративной "пирамиды", поскольку из-за их высокой себестоимости было невозможно автоматизировать решение управленческих задач. Автоматизация повторяющихся процессов обработки информации была сравнима с автоматизацией ручного труда на основе применения машин, заменивших людей. Согласно оценкам, с 1960 по 1980 г. свыше 12 млн. существовавших или потенциальных рабочих мест, связанных с обработкой информации, были автоматизированы посредством использования традиционных ЭВМ. Автоматизация рабочих мест, находившихся на нижних уровнях административной иерархии, привела к уменьшению размеров предприятий, но в то же время не вызвала кардинальных изменений в общей модели организации труда. В то время казалось маловероятным, что информационные технологии могут способствовать стабильному социально-экономическому развитию; наоборот, факты свидетельствовали о том, что их роль в повышении производительности труда, формировании моделей потребительского поведения, ориентированных на новые товары и услуги, создании новых рабочих мест в отраслях информационные технологии по сравнению с выбытием рабочих мест в отраслях - потребителях их продукции была в целом незначительной.

Виды инфы

Основные виды информации по ее форме представления, способам ее кодирования и хранения, что имеет наибольшее значение для информатики, это:

графическая или изобразительная — первый вид, для которого был реализован способ хранения информации об окружающем мире в виде наскальных рисунков, а позднее в виде картин, фотографий, схем, чертежей на бумаге, холсте, мраморе и др. материалах, изображающих картины реального мира;

звуковая — мир вокруг нас полон звуков и задача их хранения и тиражирования была решена с изобретением звукозаписывающих устройств в 1877 г. (см., например, историю звукозаписи на сайте — http://radiomuseum.ur.ru/index9.html); ее разновидностью является музыкальная информация — для этого вида был изобретен способ кодирования с использованием специальных символов, что делает возможным хранение ее аналогично графической информации;

текстовая — способ кодирования речи человека специальными символами — буквами, причем разные народы имеют разные языки и используют различные наборы букв для отображения речи; особенно большое значение этот способ приобрел после изобретения бумаги и книгопечатания;

числовая — количественная мера объектов и их свойств в окружающем мире; особенно большое значение приобрела с развитием торговли, экономики и денежного обмена; аналогично текстовой информации для ее отображения используется метод кодирования специальными символами — цифрами, причем системы кодирования (счисления) могут быть разными;

видеоинформация — способ сохранения «живых» картин окружающего мира, появившийся с изобретением кино.

 

Формы информацыы

Компьютер, помогающий человеку хранить и обрабатывать информацию, приспособлен в первую очередь для обработки текстовой, числовой, графической информации.

 

Рассмотрим только те виды информации, которые «понимают» технические устройства (в частности, компьютер).

 

Текстовая информация, например текст в учебнике, сочинение в тетради, реплика актера в спектакле, прогноз погоды, переданный по радио. Заметим, что в устном общении (личная беседа, разговор по телефону, радиопостановка спектакля) информация может быть представлена только в словесной, текстовой форме.

 

Числовая информация, например таблица умножения, арифметический пример, в хоккейном матче счет, время прибытия поезда и др. В чистом виде числовая информация встречается редко, разве что на контрольных по математике. Чаще всего используется комбинированная форма представления информации.

 

Рассмотрим пример. Вы получили телеграмму: «Встречайте двенадцатого. Поезд прибывает в восемь вечера». В данном тексте слова «двенадцатого» и «восемь» мы понимаем как числа, хотя они и выражены словами.

 

Графическая информация: рисунки, схемы, чертежи, фотографии. Такая форма представления информации наиболее доступна, так как сразу передает необходимый образ (модель), а словесная и числовая требуют мысленного воссоздания образа. В то же время графическая форма представления не даёт исчерпывающих разъяснений о передаваемой информации. Поэтому наиболее эффективно сочетание текста, числа и графики.

 

Например, при решении задач по геометрии мы используем чертеж (графика + пояснительный текст (текст) + числовые расчеты (числа).

 

Музыкальная (звуковая) информация.

 

В настоящее время мультимедийная (многосредовая, комбинированная) форма представления информации в вычислительной техники становится основной. Цветная графика сочетается в этих системах со звуком и текстом, с движущимися видеоизображением и трехмерными образами.

Сенсорная система.

Сенсорная система — часть нервной системы, ответственная за восприятие. Сенсорная система состоит из рецепторов, нейронных проводящих путей, ответственных за обработку полученных сигналов отделов головного мозга. Наиболее известными сенсорными системами являются зрение, слух, осязание, вкус и обоняние. С помощью сенсорной системы можно почувствовать такие физические свойства, как температура, вкус, звук или давление.

 

Рецепторное поле — это часть мира, на которую реагируют рецепторные органы и клетки. Например, часть мира, которую могут видеть глаза является рецепторным полем. Свет, который воспринимают палочки и колбочки глаза, также является рецепторным полем[1] . На данный момент определены рецепторные поля для зрительной, слуховой и соматосенсорной систем.

 

Колькасць инфармацыи

Количество информации можно рассматривать как меру уменьшения неопределенности знания при получении информационных сообщений.

 

Рассмотренный выше подход к информации как мере уменьшения неопределенности знания позволяет количественно измерять информацию. Существует формула, которая связывает между собой количество возможных информационных сообщений N и количество информации I, которое несет полученное сообщение:N = 2i (1.1)

 

 

Бит. Для количественного выражения любой величины необходимо сначала определить единицу измерения. Так, для измерения длины в качестве единицы выбран метр, для измерения массы - килограмм и т. д. Аналогично, для определения количества информации необходимо ввести единицу измерения.

 

За единицу количества информации принимается такое количество информации, которое содержится в информационном сообщении, уменьшающем неопределенность знания в два раза. Такая единица названа битом.

 

Если вернуться к рассмотренному выше получению информационного сообщения о результатах зачета, то здесь неопределенность как раз уменьшается в два раза и, следовательно, количество информации, которое несет сообщение, равно 1 биту.

 

Производные единицы измерения количества информации. Минимальной единицей измерения количества информации является бит, а следующей по величине единицей - байт, причем:

 

1 байт = 8 битов = 23 битов.

 

В информатике система образования кратных единиц измерения несколько отличается от принятых в большинстве наук. Традиционные метрические системы единиц, например Международная система единиц СИ, в качестве множителей кратных единиц используют коэффициент 10n, где n = 3, 6, 9 и т. д., что соответствует десятичным приставкам "Кило" (103), "Мега" (106), "Гига" (109) и т. д.

 

В компьютере информация кодируется с помощью двоичной знаковой системы, и поэтому в кратных единицах измерения количества информации используется коэффициент 2n

 

Так, кратные байту единицы измерения количества информации вводятся следующим образом:

 

1 килобайт (Кбайт) = 210 байт = 1024 байт;

 

1 мегабайт (Мбайт) = 210 Кбайт = 1024 Кбайт;

 

1 гигабайт (Гбайт) = 210 Мбайт = 1024 Мбайт.

Первичные единицы

бъёмы информации можно представлять как логарифм[2] количества состояний.

 

Наименьшее целое число, логарифм которого положителен — 2. Соответствующая ему единица — бит — является основой исчисления информации в цифровой технике.

 

Единица, соответствующая числу 3 (трит) равна бита, числу 10 (хартли) — бита.

 

Такая единица как нат (nat), соответствующая натуральному логарифму применяется в вычислительной технике[источник не указан 609 дней] в инженерных и научных расчётах. Основание натуральных логарифмов не является целым числом.

Единицы, производные от бита

 

Целые количества бит отвечают количеству состояний, равному степеням двойки.

 

Особое название имеет 4 бита — ниббл (полубайт, тетрада, четыре двоичных разряда), которые вмещают в себя количество информации, содержащейся в одной шестнадцатеричной цифре.

БайтИзмерения в байтах

Десятичная приставка Двоичная приставка

 

Следующей по порядку популярной единицей информации является 8 бит, или байт (о терминологических тонкостях написано ниже). Именно к байту (а не к биту) непосредственно приводятся все большие объёмы информации, исчисляемые в компьютерных технологиях.

 

Такие величины как машинное слово и т. п., составляющие несколько байт, в качестве единиц измерения почти никогда не используютс

Килобайт

Основная статья: Килобайт

 

Для измерения больших количеств байтов служат единицы «килобайт» = 1000 байт и «Кбайт»[3] (кибибайт, kibibyte) = 1024 байт (о путанице десятичных и двоичных единиц и терминов см. ниже). Такой порядок величин имеют, например

 

Мегабайт

Основная статья: Мегабайт

 

Единицы «мегабайт» = 1000 килобайт = 1000000 байт и «Мбайт»[3] (мебибайт, mebibyte) = 1024 Кбайт = 1 048 576 байт применяются для измерения объёмов носителей информации.

 

Объём адресного пространства процессора Intel 8086 был равен 1 Мбайт.

 

Оперативную память и ёмкость CD-ROM меряют двоичными единицами (мебибайтами, хотя их так обычно не называют), но для объёма НЖМД десятичные мегабайты были более популярны.

 

Современные жёсткие диски имеют объёмы, выражаемые в этих единицах минимум шестизначными числами, поэтому для них применяются гигабайты.

Гигабайт

Основная статья: Гигабайт

 

Единицы «гигабайт» = 1024 мегабайт = 1024000000 байт и «Гбайт»[3] (гибибайт, gibibyte) = 1024 Мбайт = 230 байт измеряют объём больших носителей информации, например жёстких дисков. Разница между двоичной и десятичной единицами уже превышает 7 %.

 

Размер 32-битного адресного пространства равен 4 Гбайт ≈ 4,295 Мбайт. Такой же порядок имеют размер DVD-ROM и современных носителей на флеш-памяти. Размеры жёстких дисков уже достигают сотен и тысяч гигабайт.

 

Для исчисления ещё больших объёмов информации имеются единицы терабайт—тебибайт (1012 и 240 соответственно), петабайт—пебибайт (1015 и 250 соответственно) и т. д.

 

Байт

принципе, байт определяется для конкретного компьютера как минимальный шаг адресации памяти, который на старых машинах не обязательно был равен 8 битам (а память не обязательно состоит из битов — см., например: троичный компьютер). В современной традиции, байт часто считают равным восьми битам.

 

Апыфметычныя и лагичныяаперацыи

Логические операции, логические связки, логические операторы, функции, преобразующие высказывания или пропозициональные формы (т. е. выражения логики предикатов, содержащие переменные и обращающиеся в высказывания при замене последних какими-либо конкретными их значениями) в высказывания или пропозициональные формы. Логические операции можно разделить на две основные группы: кванторы и пропозициональные (сентенциональные) связки. Кванторы играют для формализованных языков математической логики ту же роль, которую играют для естественного языка т. н. «количественные» («кванторные») слова: «все», «любой», «некоторый», «существует», «единственный», «не более (менее) чем», количественные числительные и т. п. Характерной особенностью кванторов является - в случае нефиктивного их применения - понижение числа свободных переменных в преобразуемом выражении: применение квантора к выражению, содержащему n свободных переменных, приводит, вообще говоря, к выражению, содержащему n - 1 свободную переменную, в частности, пропозициональную форму с одной свободной переменной применение квантора (по этой переменной) преобразует в высказывание.

 

Пропозициональные связки (в отличие от кванторов, введение которых знаменует переход к логике предикатов) употребляются уже в самой элементарной части логики - в логике высказываний. В формализованных логических и логико-математических языках они выполняют функции, вполне аналогичные функциям союзов и союзных слов, употребляемых для образования сложных предложений в естественных языках. Так, отрицание ù истолковывается как частица «не», конъюнкция & истолковывается как союз «и», дизъюнкция - как (неразделительное) «или», импликация É - как оборот «если..., то...», эквиваленция ~ - как оборот «тогда и только тогда, когда» и т. п. При этом, однако, соответствие между Логические операции и средствами естественного языка отнюдь не взаимно однозначно.Во-первых, потому, что высказывания, по определению, могут принимать лишь два «истинностных значения»: «истину» («и») и «ложь» («л»), так что пропозициональные Логические операции можно рассматривать как различные функции, отображающие некоторую область из двух элементов в себя; поэтому число различных n-местных (т. е. от n аргументов) Логические операции определяется из чисто комбинаторных соображений - оно равно 2n. Во-вторых, в формализованных языках математической логики игнорируются любые смысловые (и тем более стилистические) оттенки значений союзов, кроме тех, что непосредственно определяют истинностное значение получающегося сложного предложения.

 

Коньюнкция.

Конъю́нкция (от лат. conjunctio союз, связь) — логическая операция, по своему применению максимально приближённая к союзу "и". Синонимы: логи́ческое "И", логи́ческоеумноже́ние, иногда просто "И"

нкция истинна только в случае, когда оба входящих в нее высказывания являются истинными; если хотя бы один из ее членов ложен, то и вся конъюнкция ложна.

Обозначим конъюнкцию символом &. Таблица истинности для конъюнкции приведена ниже.

А В А & В

и и и

и л л

л и л

л л л

Отрицание – логическая связка, с помощью которой из данного высказывания получается новое, причем, если исходное высказывание истинно, его отрицание будет ложным, и наоборот. Отрицательное высказывание состоит из исходного высказывания и отрицания, выражаемого обычно словами "не", "неверно, что". Отрицательное высказывание является, таким образом, сложным высказыванием: оно включает в качестве своей части отличное от него высказывание. Например, отрицанием высказывания "10 – четное число" является высказывание "10 не есть четное число" (или:"Неверно, что 10 есть четное число")..

Соединяя два высказывания с помощью слова "или", мы получаем дизъюнкцию этих высказываний. Высказывания, образующие дизъюнкцию, называются членами дизъюнкции.

Слово "или" в повседневном языке имеет два разных смысла. Иногда оно означает "одно или другое или оба", а иногда "одно или другое, но не оба вместе". Высказывание "В этом сезоне я хочу пойти на "Пиковую даму" или на "Аиду"" допускает возможность двукратного посещения оперы. В высказывании же "Он учится в Московском или в Саратовском университете" подразумевается, что упоминаемый человек учится только в одном из этих университетов.

Первый смысл "или" называется неисключающим. Взятая в этом смысле дизъюнкция двух высказываний означает только, что по крайней мере одно из этих высказываний истинно, независимо от того, истинны они оба или нет. Взятая во втором, исключающем, смысле дизъюнкция двух высказываний утверждает, что одно из них истинно, а второе – ложно.

Символ v будет обозначать дизъюнкцию в неисключающем смысле, для дизъюнкции в исключающем смысле будет использоваться символ V. Таблицы для двух видов дизъюнкции показывают, что неисключающая дизъюнкция истинна, когда хотя бы одно из входящих в нее высказываний истинно, и ложна, только когда оба ее члена ложны; исключающая дизъюнкция истинна, когда истинным является только один из ее членов, и она ложна, когда оба ее члена истинны или оба ложны.

А В A v В A V B

и и и л

и л и и

л и и и

л л л л

Импликация

Условное высказывание находит очень широкое применение во всех сферах рассуждения. В логике оно представляется, как правило, посредством импликативного высказывания, или импликации. При этом логика проясняет, систематизирует и упрощает употребление связки "если ..., то ...", освобождает его от влияния психологических факторов.

 

Логика отвлекается, в частности, от того, что характерная для условного высказывания связь основания и следствия в зависимости от контекста может выражаться не только с помощью связки "если ..., то ...", но и с помощью других языковых средств. К примеру: "Так как вода жидкость, она передает давление во все стороны равномерно", "Хотя пластилин и не металл, он пластичен", "Если бы дерево было металлом, оно было бы электропроводно" и т.п. Эти и подобные им высказывания представляются в языке логики посредством импликации, хотя употребление в них "если ..., то ..." было бы не совсем естественным.

 

Утверждая импликацию, мы утверждаем, что не может случиться, чтобы ее основание (антецедент) было истинным, а следствие (консеквент) – ложным.

 

Это определение как и предыдущие определения связок предполагает, что всякое высказывание является либо истинным, либо ложным и что истинностное значение сложного высказывания зависит только от истинностных значений составляющих его высказываний и способа их связи.

 

Для установления истинности импликации "если А, то В" достаточно, таким образом, выяснить истинностные значения высказывании А и В. Из четырех возможных случаев импликация истинна в следующих трех:

 

(1) и ее основание, и ее следствие истинны;

(2) основание ложно, а следствие истинно;

(3) и основание, и следствие ложны.

Только в четвертом случае, когда основание истинно, а следствие ложно, вся импликация ложна.

Будем обозначать импликацию символом →. Таблица истинности для импликации приводится.

А В A → В

и и и

и л л

л и и

л л и

 

 

Смысл импликации, как одной из логических связок, полностью определен этой таблицей, и ничего другого импликация не подразумевает.

Эквивалентность — сложное высказывание «А, если и только если В», образованное из высказываний А и В и разлагающееся на две импликации: «если А, то В» и «если В, то А». Например: «Треугольник является равносторонним, если и только если он является равноугольным». Термином «эквивалентность» обозначается и связка «..., если и только если ...», с помощью которой из двух высказываний образуется данное сложное высказывание. Вместо «..., если и только если ...» для этой цели могут использоваться «... в том и только том случае, когда ...», «... тогда и только тогда, когда ...» и т. п.

Личбавыя аутаматы

ЦА представляет собой последовательностную схему и служит для обработки

дискретной информации.

В операционном устройстве выполняются арифметические и логические

операции, в качестве узлов в состав операционного устройства входят:

регистры, счетчики, сумматоры, дешифраторы и др. Управляющие устройства

координируют действия узлов операционного устройства, оно определенной

временной последовательности вырабатывает управляющие сигналы под

действием которых в узлах операционного устройства выполняются требуемые

функции.

Процессорное устройство описывается множеством входных сигналов

являющихся исходными данными. Множеством результатов Z1-Zm, управляющее

устройство вырабатывает множество управляющих сигналов y1-yn,

операционное устройство вырабатывает множество признаков X1-Xs, которые

позволяют изменить последовательность выполненных микрокоманд. На

последовательность выполнения микрокоманд так же влияют внешние признаки

Xs+1-XL.

2. АЛГОРИТМ ФУНКЦИОНИРОВАНИЯ ЦИФРОВОГО АВТОМАТА

В состав процессорного устройства входят регистры, счетчики и

дешифратор. Пусть регистр Р1 хранит число А. В регистр Р2 поочередно

заносятся элементы проверяемого массива, счетчик 1 служит для подсчета

числа циклов. Счетчик 2 служит для подсчета числа элементов =А.

Дешифратор используется для формирования признака х. Алгоритм

функционирования автомата в микрооперациях представлен на рис.2

 

Под действием управляющего сигнала y1 в регистр Р1 записывается

проверяемое число х. Под действием управляющего сигнала y2 в регистр R2

записывается число B. Под действием управляющего сигнала y3 в регистре

R3 записываются число А ив сумматоре 1 сравнивается числа Аи х. На

выходе переноса сумматора вырабатывается признак х. Если х<А то признак

х=1 и выполняется переход на формирование управляющего сигнала y5, если

наоборот то х=0 и выполняется переход на формирование управляющего

импульса у4. Под действием управляющего сигнала y5 в сумматоре 2 должен

быть организован режим сложения и в нем вычисляется х+В. Под действием

управляющего сигнала у4 в сумматоре должен быть организован режим

вычитания и вычисляется х-В. Под действием управляющего сигнала у6

результат полученный в сумматоре 2 записывается в регистр R4.

3. СТРУКТУРНАЯ СХЕМА ОПЕРАЦИОННОГО УСТРОЙСТВА.

 

Так как регистры используются для записи чисел массива, поэтому в них

должен быть организован режим параллельной загрузки.

Т.к. сумматор 1 используется для сравнения чисел то в нем должен быть

организован режим вычитании. Сумматор 2 используется для вычисления х-В

и х+В и в нем организуется режим вычитания и сложения.

 

 

Булевы аперацыи

1. Конъюнкция и дизъюнкция.

 

Дизъю́нкция — логическая операция, по своему применению максимально приближенная к союзу «или» в смысле «или то, или это, или оба сразу». Синонимы: логи́ческое «ИЛИ», включа́ющее «ИЛИ», логи́ческоесложе́ние, иногда просто «ИЛИ».

 

Это бинарная инфиксная операция, то есть, она имеет два операнда и стоит между ними. Чаще всего встречаются следующие варианты записи:

 

В булевой алгебре дизъюнкция — это функция двух переменных (они же — операнды операции). Переменные Правило: результат равен , если оба операнда равны ; во всех остальных случаях результат равен .Таблица истинности

 

Конъю́нкция — логическая операция, по своему применению максимально приближенная к союзу "и". Синонимы: логи́ческое "И", логи́ческоеумноже́ние, иногда просто "И".

 

Это бинарная инфиксная операция, то есть, она имеет два операнда и ставится между ними. Чаще всего встречаются следующие варианты записи:

&&& .

По аналогии с умножением в алгебре знак логического умножения может быть пропущен: .

Таблица истинности

 

В булевой алгебре конъюнкция - это функция двух переменных (они же - операнды операции). Переменные могут принимать значения из множества . Результат также принадлежит множеству . Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений может использоваться любая другая пара подходящих символов, например или или "ложь", "истина".

 

Правило: результат равен , если оба операнда равны ; во всех остальных случаях результат равен .

 

Таблица истинности:

 

 

Импликация — бинарная логическая связка, по своему применению приближенная к союзам «если… то…».

 

Импликация записывается как посылка следствие; применяются также стрелки другой формы и направленные в другую сторону (остриё всегда указывает на следствие). Суждение, выражаемое импликацией, выражается также следующими способами:

Посылка является условием, достаточным для выполнения следствия;

Следствие является условием, необходимым для истинности посылки.

Импликация как булева функция ложна лишь тогда, когда посылка истинна, а следствие ложно. Иными словами, импликация — это сокращённая запись для выражения.

 

Пусть A1, A2 – есть две формулы, x1, x2,…,xn – есть полный список или множество их переменных. Формулы A1, A2 – называются равносильными или эквивалентными ⇔, если для любого набора значений аргументов x1, x2,…,xn, они принимают одинаковые значения.

Свойства!!!!!

Замечание: В инженерной практике наиболее распространены представления функций формулами, построенными с помощью конъюнкции, дизъюнкции, отрицания и констант 0,1 т.е. формулами над F={x&y, x∨y,x,0, 1}, такие формы называются Булевыми. Иногда в F включают импликацию. Примем соглашение об опускании скобок в соответствии со следующими приоритетами:

Пусть А,В,С – некоторые булевы формулы. Тогда справедливы следующие свойства:

1) A&A = A, A∨A = A – идемпотентность.

2) A&B = B&A, A∨B = B∨A – коммуттативность