Тема: Програмування для обчислювальних систем з фiксованою кiлькiстю потокiв.
Мета: Опанувати методику створення багатопоточних додаткiв для систем з загальною пам'ятю.
Постановка задачi
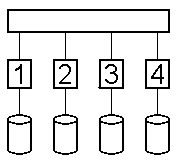
Розробити паралельну програму наведеної структури для матричних обрахункiв використовуючи засувки для керування процесами доступу до загальних ресурсiв (у загальної пам'ятi).
Ця програма повинна забезпечувати ввод даних вiдповiдними процесами (пристроями вводу/виводу), їх розподiл на незалежнi фрагменти, органiзацiю та запуск паралельних обчислювальних процесiв, збирання результатiв обчислень та формування i виведення результатiв.
Вимоги до звiту
Iндивiдуальнi завдання для самостiйної роботи
| Варiант | Дiя | Опис даних | Пристрiй вводу / виводу | |||
| A = B * MC | A, B - вектори, MC - матриця. | A | B | MC | ||
| A = (B + Z) * MX | A, B, Z - вектори, MX - матриця. | A | B, Z | MX | ||
| MA = a * (MB + MC) | MA, MB, MC - матрицi, a - константа. | MB | MA | MC | a | |
| MA = MB * MC - a * MX | MA, MB, MC, MX - матрицi, a - константа. | MA, a | MC | MB, MX | ||
| a = max(B * MZ) | B - вектор, MZ - матриця, a - число. | a | B | MZ | ||
| a = min(E * MT - MZ) | E - вектор, MT, MZ - матрицi, a - число. | a | E | MT | MZ | |
| A = B * (MX + MY) | A, B - вектори, MX, MY - матрицi. | MY | MX | A | B | |
| MA = MB * (MZ - MO) | MA, MB, MO, MZ - матрицi. | MA | MB | MO | MZ | |
| a = (B * (C + Z)) | B, C, Z - вектори, a - число. | a | B | C | Z | |
| MA = a * MO * (MB - MZ) | MA, MB, MZ, MO - матрицi, a - константа. | MA, a | MB | MZ | MO | |
| A = (B + C) * (MX - MY) | A, B, C - вектори, MX, MY - матрицi. | A, C | B | MX | MY | |
| A = (B - C + D) * MO | A, B, C, D - вектори, MO - матриця. | C | B, D | A | MO | |
| MX = MY * (MR - a * MT) | MX, MY, MR, MT - матрицi, a - константа. | a, MY | MR | MT | MX | |
| Z = B * MO - a * R | B, R, Z - вектори, MO - матриця, a - константа. | R, Z | a | MO | B | |
| MA = MB * (MZ - ME * MT) | MA, MB, ME, MT, MZ - матрицi. | MA, MZ | MB | ME | MT | |
| a = max(MB - a * MZ) | a - число, MB, MZ - матрицi, a - константа. | a | MB | a | MZ | |
| a = min(a * MO + MT) | a - число, MO, MT - матрицi, a - константа. | a | a | MO | MT | |
| a = a * min(MT * ME) | a - число, MT, ME - матрицi, a - константа. | a | a | MT, ME | ||
| a = max(B * MT + ME) | a - число, B - вектор, MT, ME - матрицi. | a | MT, ME | B | ||
| MA = (MB * MZ) + a * MR | MA, MB, MZ, MR - матрицi, a - константа. | MA, MB | a | MZ | MR | |
| MA = a * (MB * MZ) - MR | MA, MB, MZ, MR - матрицi, a - константа. | MA, a | MZ | MB | MR | |
| MA = a * (MB + MZ * MO) | MA, MB, MZ, MO - матрицi, a - константа. | MZ, a | MA | MO | MB | |
| MA = a * MX + MZ * MO | MA, MX, MZ, MO - матрицi, a - константа. | MA | a, MX | MZ | MO | |
| MA = a * MB + b * MC + g * MD | MA, MB, MC, MD - матрицi, a, b, g - константи. | a, b, g, MA | MB | MC | MD | |
| MA = a * (b * MB + g * MC) | MA, MB, MC - матрицi, a, b, g - константи. | a, MA | MB | b, g | MC | |
| a = max(a * MA + b * MB) | a - число, MA, MB - матрицi, a, b - константи. | a | MA | a, b | MB | |
| MA = a * MB + b * (MC + g * MD) | MA, MB, MC, MD - матрицi, a, b, g - константи. | a, MA | MB | b, g, MC | MD | |
| MA = MB * (a * MC + b * MD) | MA, MB, MC, MD - матрицi, a, b - константи. | a, b, MA | MB | MC | MD | |
| A = B * MB + C * (MC + a * MD) | A, B, C - вектори, MB, MC, MD - матрицi, a - константа. | a, A, B, C | MB | MC | MD | |
| MA = MB * MC - a * MD | MA, MB, MC, MD - матрицi, a - константа. | a, MA | MB | MC | MD | |
| a = a * max(MA * MB - b * MC) | a - число, MA, MB, MC - матрицi, a, b - константи. | a, a, b | MA | MB | MC |
Самостiйна робота №2.
Тема: Програмування для обчислювальних систем зi змiнною кiлькiстю процесiв.
Мета: Опанувати методику створення багатопоточних додаткiв для систем з загальною пам'ятю.
Постановка задачi
Розробити паралельну програму, яка використовує декiльлька процесiв для вирiшення поставленої задачi.
Ця програма повинна забезпечувати ввод даних вiдповiдними процесами (пристроями вводу/виводу), їх розподiл на незалежнi фрагменти, органiзацiю та запуск паралельних обчислювальних процесiв, збирання результатiв обчислень та формування i виведення результатiв.
Кiлькiсть процесiв задавати як параметр при запуску програми.
Побудувати графiк залежностi часу виконання програми вiд кiлькостi процесiв, що її виконують.
Виконати обрахунок теоретичного коефiцiєнту прискорення.
Вимоги до звiту
Iндивiдуальнi завдання для самостiйної роботи
- Дано дві матриці A[n, n] і B[n, n], їх треба проініціалізувати значенням 1.0, скласти i результат покласти у матрицю C[n, n]. Тобто виконати операцiю:
C[i, j] = A[i, j] + B[i, j], де 0 < i < n, 0 < j < n.
Напишить паралельну програму для рішення цієї задачи. Обчислить смуги результату паралельно, використовуючи n робочих потоків.
- Для рішення задачи квадратури, напишить паралельну ітеративну програму з фиксованим числом інтервалів. Проінтегруйте функцію з графіком f(x) = sin(x) * exp(x). Ваша програма повинна використовувати параметри командного рядка для інтервала значень х (числа відрізків).
- Для рішення задачи квадратури, напишить паралельну рекурсивну програму, що використовує адаптивну квадратуру. Проинтегруйте функцію з графіком f(x) = sin(x) * exp(x). Ваша програма повинна використовувати параметри командного рядка для значення epsilon.
- Напишить паралельну рекурсивну програму для реалізації алгоритму швиткого сортування массиву з N чисел. Будьте уважними, щоб забезпечити незалежність паралельных викликів.
- Матриця T є транспонованою матрицею M, якщо для усіх значень i і j виконується рівняння T[i, j] = M[j, i]. Напишить паралельну програму, яка з використанням розподілюваних змінних транспонує матрицю М розміром n х n. Використовуйте P робочих потоків. Для спрощення припустимо, що число n кратно Р.
- Матриця T є транспонованою матрицею M, якщо для усіх значень i і j виконується рівняння T[i, j] = M[j, i]. Напишить паралельну програму, яка з використанням розподілюваних змінних транспонує матрицю М розміром n х n. Використовуйте P робочих потоків. Для спрощення припустимо, що число n не кратно Р.
- Напишить просту программу, яка виконує пошук заданого шаблону у файлах і використовує два аргумента: ланцюжок символів і им'я файлу. Усі рядки файла зі знайденим ланцюжком символів програма повинна виводити у файл. Змінити програму так, щоб вона виконувала пошук у двох файлах паралельно. Обидва процеса повинні виводити дані у файл stdout.
- Напишить паралельну програму для пошуку максимального элемента у массиві цілих чисел A[n]. Під час пошуку масив розподіляється на частини і кожна частина обробляється окремим потоком.
- Напишить паралельну програму для копіюваня масива A[n] у масив B[n]. Для синхронізації роботи використовуйте один буфер. Перший поток повинен читати дані з масиву A[n] у буфер. Другий поток повинен читати дані з буферу та записувани їх у масив B[n].
- Дано два масиви A1 i A2 довжиною N. Реалiзувати паралельну процедуру поелементного складання цих масивiв P = A1 + A2. Для цього задiяти N/4 потоки.
- Дано масив A довжиною N. Реалiзувати паралельну процедуру його бульбашкового сортування. Для цього задiяти N/6 потокiв.
- Дано масив A довжиною N. Реалiзувати паралельну процедуру пiдрахунку середнього його елементiв. Для цього задiяти N/8 потокiв.
- Дано масив A довжиною N. Реалiзувати паралельну процедуру обчислення медiани його елементiв. Для цього задiяти N/5 потокiв.
- Дано масив A довжиною N. Реалiзувати паралельну процедуру iнверсiї його елементiв. Для цього задiяти N/7 потокiв.
- Напишить паралельну програму, яка генерує послiдовнiсть Фiбоначчi довжиною N. Сгенерованi числа зберiгаються у загальному масивi. Використайте два потоки, якi почергово отримують доступ до цього масиву. Пiсля закiнчення процесу генерацiї, третiй потiк повинен вивести результат на екран.
- Дана матриця, яка складається з M стовпцiв та N рядкiв (M > N). Розробити паралельну програму, яка використовуючи M паралельних потокiв шукає максимальне значення матрицi. Результатом роботи програми повинно бути знайдене число та його адреса (номери стовпця та рядка).
- Дана матриця, яка складається з M стовпцiв та N рядкiв (M > N). Розробити паралельну програму, яка використовуючи N паралельних потокiв шукає мiнiмальне значення матрицi. Результатом роботи програми повинно бути знайдене число та його адреса (номери стовпця та рядка).
- Написати паралельну програму обернення матрицi розмiрнiстю N x N використовуючи 2 * N - 3 паралельнi потоки.
- Написати паралельну програму обернення матрицi розмiрнiстю N x N використовуючи 2 паралельних потоки, а також потiк для введення даних iз зовнiшнього файлу, та потiк для виведення результату.
- Мiшаний граф G з n вершинами заданий матрицею сумiжностi вершин. Написати паралельну програму, яка пiдраховує кiлькiсть орiєнтованих ребер у ньому. Задiяти для цього 2 * n - 3 паралельнi потоки.
- Мiшаний граф G з n вершинами заданий матрицею сумiжностi вершин. Написати паралельну програму, яка пiдраховує кiлькiсть орiєнтованих ребер у ньому. Задiяти для цього n - 1 паралельний потiк.
- Граф G з n вершинами заданий матрицею сумiжностi вершин. Написати паралельну програму, яка перевiряє, чи э вiн повним. Задiяти для цього 2 * n - 3 паралельнi потоки.
- Граф G з n вершинами заданий матрицею сумiжностi вершин. Написати паралельну програму, яка перевiряє, чи э вiн повним. Задiяти для цього n - 1 паралельний потiк.
- Написати паралельну програму, яка пiдраховує довжину траєкторiї, пройденої матерiальною точкою за час T. Закон руху точки у полярних координатах є таким:
R = a * sin(w * T + phi).
Використати парну кiлькiсть паралельних потокiв.
- Написати паралельну програму, яка пiдраховує довжину траєкторiї, пройденої матерiальною точкою за час T. Закон руху точки у полярних координатах э таким:
R = a * sin(w * T + phi).
Використати непарну кiлькiсть паралельних потокiв.
Самостiйна робота №3.