Тема: Програмування для обчислювальних систем з локальною пам'ятю ("Рандеву").
Мета: Опанувати методику створення багатопоточних додаткiв.
Постановка задачi
Розробити паралельну програму наведеної структури для матричних обрахункiв використовуючи принцип "Рандеву".
Ця програма повинна забезпечувати ввод даних вiдповiдними процесами (пристроями вводу/виводу), їх розподiл на незалежнi фрагменти, органiзацiю та запуск паралельних обчислювальних процесiв, збирання результатiв обчислень та формування i виведення результатiв.
Пiд час розробки програми використати обмiнники для передачi даних мiж паралельними процесами з локальною пам'ятю.
Вимоги до звiту
Iндивiдуальнi завдання для самостiйної роботи
| Варiант | Конфiгурацiя | Дiя | Опис даних | Пристрiй вводу / виводу | |||||
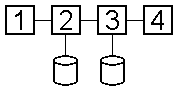
| A = B * MC | A, B - вектори, MC - матриця. | A, B | MC | |||||
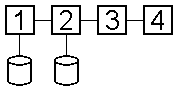
| MA = MB * MC | MA, MB, MC - матрицi. | MA, MB | MC | |||||

| MA = MB + MC * MZ | MA, MB, MC, MZ - матрицi. | MA, MC | MB, MZ | |||||

| a = max(MB * MC) | MB, MC - матрицi, a - число. | a, MB, MC | ||||||

| a = min(B * MZ) | MZ - матриця, B - вектор, a - число. | a, MB, MC | ||||||

| A = (B + C) * MZ | MZ - матриця, A, B, C - вектори. | A, B | C, MZ | |||||

| A = B * (MX - MZ) | MX, MZ - матрицi, A, B - вектори. | A, B, MX, MZ | ||||||

| A = B + C * MZ | MZ - матриця, A, B, C - вектори. | A, C | B, MZ | |||||

| MA = MB * MC | MA, MB, MC - матрицi. | MA, MB | MC | |||||

| A = B - C * MZ | MZ - матриця, A, B, C - вектори. | A, C | B, MZ | |||||

| MA = MB * MC | MA, MB, MC - матрицi. | MA, MB, MC | ||||||

| A = B + C * MX | MX - матриця, A, B, C - вектори. | B, MX | A, C | |||||

| MX = MY * MZ | MX, MY, MZ - матрицi. | MX, MY | MZ | |||||

| a = max(MB * MZ) | MB, MZ - матрицi, a - число. | a, MB | MZ | |||||

| MA = MB + MC * MZ | MA, MB, MC, MZ - матрицi. | MA, MC | MB, MZ | |||||

| A = (B + C) * MZ | MZ - матриця, A, B, C - вектори. | A, C | B, MZ | |||||

| MA = MB + MC * MZ | MA, MB, MC, MZ - матрицi. | MA, MC | MB, MZ | |||||

| a = max(MB * MZ) | MB, MZ - матрицi, a - число. | MZ | a, MB | |||||

| A = B * MX | MX - матриця, A, B - вектори. | A, B, MX | ||||||

| A = (B + C) * MZ | MZ - матриця, A, B, C - вектори. | A, B, C | MZ | |||||

| MA = (MB * MZ) | MA, MB, MZ - матрицi. | MA | MB, MZ | |||||

| A = B + C * MX | MX - матриця, A, B, C - вектори. | A, B, C, MX | ||||||

| MZ = MX * MY | MX, MY, MZ - матрицi. | MX | MZ, MY | |||||

| A = B + C * MZ | MZ - матриця, A, B, C - вектори. | A, C | B | MZ | ||||

| MA = MB * MC | MA, MB, MC - матрицi. | MA | MB | MC | ||||

| MA = a * (MB + MZ * MO) | MA, MB, MZ, MO - матрицi, a - константа. | MZ, a MA MO MB | ||||||

| MA = a * MX + MZ * MO | MA, MX, MZ, MO - матрицi, a - константа. | MZ MO | MA a, MX | |||||

| MA = a * MB + b * MC + g * MD | MA, MB, MC, MD - матрицi, a, b, g - константи. | MA MD | a, b, g, MB MC | |||||

| MA = a * MB + b * (MC + g * MD) | MA, MB, MC, MD - матрицi, a, b, g - константи. | a, b, g, MA MC | MB MD | |||||

| MA = MB * (a * MC + b * MD) | MA, MB, MC, MD - матрицi, a, b - константи. | MB MC | a, b, MA MD | |||||

| MA = a * MO * (MB - MZ) | MA, MB, MZ, MO - матрицi, a - константа. | MO | MB MZ | MA, a |
Додатковi завдання для пiдвищення балiв
з курсу
“Паралельне програмування”
- Заповнити одновимiрний масив значенням v, використовуючи чотири процеси. Значення v ввести як параметр у командному рядку.
- За допомогою чотирьох паралельних процесiв пiдрахувати кiлькiсть елементiв, якi мають значення iстина, у одновимiрному булевому масивi.
- За допомогою чотирьох паралельних процесiв пiдрахувати кiлькiсть елементiв, якi мають значення iстина, у двовимiрнiй булевiй матрицi.
- За допомогою чотирьох паралельних процесiв пiдрахувати кiлькiсть елементiв, якi мають значення iстина, у тривимiрному булевому кубi даних.
- За допомогою чотирьох паралельних процесiв у цiлочисельному масивi знайти середнє арифметичне.
- За допомогою чотирьох паралельних процесiв у цiлочисельному масивi знайти медiану (середнє найменшого й найбiльшого значень).
- Виконати iнверсiю елементiв одновимiрного масиву за допомогою шести паралельних процесiв.
- Пiдрахувати суму елементiв цiлочисельної матрицi за допомогою шести паралельних процесiв.