Декартова прямоугольная система координат

Основные понятия
 
 
B
A

Геометрическим вектором называется направленный отрезок 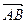с начальной точкой A и конечной В.

Длиной вектора 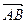называется неотрицательное число, равное длине отрезка AB, соединяющего точки A и B. Обозначается .

Если точки A и B совпадают, то вектор называется нулевым.

Вектора, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.

Два вектора называются равными, если они коллинеарные, имеют одинаковую длину и одинаковое направление.

 

Линейные операции над векторами

1. Сложение векторов

 

·

по правилу треугольника

 
 

 

 


· по правилу параллелограмма

 

 
 

 

 


2.

Разность векторов

 

 

3. Умножение вектора на число

 

Произведением вектора на число называется вектор , коллинеарный вектору , имеющий длину и направление, совпадающее с , если и противоположное, если .

 

Проекция вектора на ось

B
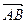Проекцией вектора на ось u называется отрезок , где точка – проекция точки A, точка – проекция точки B.

 
 

 


Если продолжить вектор до пересечения с осью u, то – угол наклона вектора 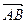к оси u.

. (3.1)

 

Основные свойства проекций:

 

· при сложении двух и более векторов их проекции на произвольную ось складываются, т.е. ;

· при умножении вектора на число его проекция умножается на это число, т.е. .

 

Декартова прямоугольная система координат

 

Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях Ox (абсцисс), Oy (ординат) и Oz (аппликат) единичные вектора (орты) .

 

Выберем произвольный вектор пространства и совместим его начало с началом координат. Тогда разложение вектора по ортам координатных осей имеет вид:

, (3.2)

где x, y, z – координаты вектора , проекции вектора на соответствующие координатные оси.

Если даны две точки и , являющиеся соответственно началом и концом вектора , то его координаты определяются по формулам:

. (3.3)

Модуль (длина) вектора может быть вычислен по формуле:

 

. (3.4)

Если — углы, которые составляет вектор с координатными осями, то называются направляющими косинусами вектора.

 

 

Координаты вектора могут быть вычислены по формулам

, , . (3.5)

Для любого вектора справедлива формула:

. (3.6)

 

Действия над векторами, заданными своими координатами.

 

Пусть два вектора и заданы своими координатами, тогда

· при сложении (вычитании) этих векторов их одноименные координаты складываются (вычитаются) ;

· при умножении вектора на число координаты ветора умножаются на это число ;

· два вектора равны тогда и только тогда. Когда равны их одноименные координаты, т.е. ;

· если вектора коллинеарны, то их координаты пропорциональны, и наоборот, т.е. и – коллинеарные , где k – коэффициент пропорциональности, .