Скалярное произведение векторов
Скалярным произведением двух ненулевых векторов и называется число, равное про­изведению модулей этих векторов на косинус угла между ними.

, (3.7)

где .

Скалярное произведение векторов и можно выразить также формулой

, (3.8)

 

Свойства скалярного произведения векторов:

· ;

· ;

· ;

· ;

· если , , тогда .

Если векторы и заданы своими координатами , и , то их скалярное произведение может быть вычислено по формуле

. (3.9)

Отсюда следует необходимое и достаточное условие перпендикулярности векторов:

. (3.10)

 

Некоторые приложения скалярного произведения:

 

1. угол между векторами , и можно вычислить по формулам:

или (3.11)

2. проекция произвольного вектора на направление, заданное вектором , может быть вычислена по формулам:

или . (3.12)

 

3. работа постоянной силы при прямолинейном перемещении ее точки приложения вдоль вектора может быть найдена по формуле:

, (3.13)

где .

Пример. Вектора и образуют угол . Зная, что , найти угол между векторами и .

Найдем

. Аналогично .

Таким образом, . Следовательно, .

Векторное произведение векторов
Определение. Три вектора называются упорядоченной тройкой, если указано какой вектор – первый, какой – второй, какой – третий. При записи вектора будут располагаться в порядке их следования.

Определение. Тройка некомпланарных векторов называется правой (левой), если будучи приведенными к одному началу, они располагаются так, как расположены соответственно большой, указательный и средний пальцы правой (левой) руки.

 
 
 

 


 

 

правая тройка

 

 

 

 

левая тройка

Определение. Векторным произведением двух векторов и называется вектор , обозначаемый символом и удовлетворяющий следующим условиям:

· ;

· вектора , , образуют правую тройку векторов;

· длина вектора определяется по формуле , где .

Свойства векторного произведения векторов:

· ;

· ;

· ;

· ;

Если векторы и заданы своими координатами , и , то их векторное произведение может быть вычислено по формуле

. (3.14)

Некоторые приложения векторного произведения:

1. если вектора и - коллинеарны, то (и наоборот);

2. длина векторного произведения численно равна площади параллелограмма, построенного на приведенных к общему началу векторах и ;

3. момент постоянной силы , приложенной к точке M , относительно точки O может быть найден по формуле:

. (3.15)

 

Пример. Вычислить площадь треугольника с вершинами .

Найдем координаты векторов, на которых построен треугольник и . Тогда их векторное произведение можно посчитать следующим образом

Площадь параллелограмма, построенного на векторах 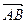и , численно равна длине их векторного произведения, т.е. .

Таким образом, .