Приклади розв’язування задач. (коливання і хвилі, хвильова і квантова оптика)
О.С. Камінський
ЗБІРНИК ЗАДАЧ З ФІЗИКИ
Частина 2
(коливання і хвилі, хвильова і квантова оптика)
Міністерство освіти і науки України
Вінницький національний технічний університет
С.Г. Авдєєв, Т.І. Бабюк,
О.С. Камінський
ЗБІРНИК ЗАДАЧ З ФІЗИКИ
Частина 2
(коливання і хвилі, хвильова і квантова оптика)
Вінниця ВНТУ 2009
Частина 2
Розділ 1. Гармонічні коливання і хвилі
Основні формули
1. Зміщення, швидкість і прискорення матеріальної точки при гармонічних коливаннях визначаються рівняннями:
х = А cos (w t + j0),
υ = - A w sin (wt + j0),
a = - A w2cos (wt + j0) = - w2 x,
де А - амплітуда коливань;
w - циклічна частота;
j0 - початкова фаза коливань.
2. Зв’язок циклічної частоти w з періодом коливань Т і частотою n:
w =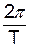 
= 2 p n.
3. Сила, яка діє на тіло при вільних гармонічних коливаннях (квазіупружна сила):
F = ma = - m w2 x = - k x,
де k = mw2 - коефіцієнт квазіупружної сили, який вимірюється силою, що визиває зміщення х = 1.
4. Кінетична, потенціальна і повна енергії гармонічних коливань матеріальної точки:
,
,
.
5. Диференціальні рівняння малих коливань:
а) математичний маятник
+ 
x = 0, де 
, звідки T = 2p 
;
б) пружинний маятник
+ 
x = 0, де 
, звідки Т = 2p 
;
в) фізичний маятник
+ 
x = 0, де 
, звідки T = 2p 
,
де І - момент інерції маятника відносно осі коливань;
l - відстань від осі коливань до центра мас маятника;
- приведена довжина.
При відсутності опору середовища циклічна частота коливань w називається власною циклічною частотою і позначається через w0.
6. При додаванні двох однаково направлених гармонічних коливань однакового періоду одержуємо гармонічне коливання того ж періоду, амплітуда якого А і початкова фаза j0 визначаються рівняннями:
,
tq j0 = 
,
де А1 і А2 - амплітуди коливань, що складаються;
j1 і j2 - початкові фази цих коливань.
7. При додаванні двох однаково направлених гармонічних коливань однакової амплітуди і близьких частот (w1 » w2) одержуємо биття, яке описується рівнянням:
x = 
cos 
,
де 
- амплітуда биття.
Періодичність зміни амплітуди визначається періодичністю зміни модуля косинуса, тому період биття дорівнює:
Tб = p , звідки Tб = 
.
8. При додаванні двох взаємно перпендикулярних гармонічних коливань з однаковою частотою в напрямі координатних осей х і у матимемо рівняння траєкторії результуючого руху матеріальної точки:
cos(j2 - j1) = sin2 (j2 - j1),
де А1 і А2 - амплітуди коливань, що додаються;
j2 - j1 - різниця фаз цих коливань.
9. Диференціальне рівняння загасаючих коливань :
0, або
де b = 
- коефіцієнт загасання;
r - коефіцієнт опору середовища;
- власна циклічна частота коливань.
10. Загальний розв’язок диференціального рівняння для загасаючих коливань має вигляд:
x = A0e-bt cos (wt + a),
де А0е-bt - амплітуда загасаючих коливань;
w - циклічна частота загасаючих коливань.
11. Швидкість зменшення амплітуди загасаючих коливань характеризують логарифмічним декрементом загасання
δ= ln 
,
де δ - логарифмічний декремент загасання;
b - коефіцієнт загасання;
Т - період загасаючих коливань.
12. Циклічна частота загасаючих коливань
w = 
, або w = 
.
13. Період загасаючих коливань:
T = 
, або Т = 
.
14. Добротність коливальних систем
q = 2p 
, або q = 
,
де Wt - повна енергія, яку має коливальна система на момент часу t;
DW(t=T) - втрати енергії коливальної системи за один період; δ - логарифмічний декремент загасання;
b - коефіцієнт загасання;
w0 - власна циклічна частота коливань;
Т - період загасаючих коливань (при малих загасаннях Т » Т0).
15. Диференціальне рівняння вимушених коливань
,
або
де F0 - вимушувана сила;
w - циклічна частота вимушених коливань.
16. Загальний розв’язок диференціального рівняння вимушених коливань, які протягом певного часу встановлюються під дією вимушуваної сили має вигляд:
x = A cos (wt + a)
де А - амплітуда вимушених коливань;
a - зсув за фазою вимушених коливань і вимушуваної сили.
17. Амплітуда вимушених коливань
A = 
,
де f0 = 
;
w0 - власна частота коливань системи;
w - циклічна частота вимушуваної сили.
18. Зсув фази вимушених коливань:
tga = - 
.
19. Резонансна частота і резонансна амплітуда:
wрез = 
;
Арез = 
.
Приклади розв’язування задач
Приклад 1. Частинка здійснює гармонічні коливання вздовж осі х біля положення рівноваги х = 0. Циклічна частота коливань w = 4 c-1. В момент часу t = 0 координати частинки х0 = 25,0 см, а її швидкість v= 100 см/с. Знайти координату х і швидкість υ цієї частинки через t = 2,40 с.
Дано:
w = 4 с-1
х0 = 25,0 см
υ= 100,0 см/с
t = 2,40 с
------------------------------
х = ? υ= ?
Розв’язування: Рівняння гармонічних коливань має вигляд:
x = Acos (w t + j). (1)
Швидкість частинки в довільний момент часу дорівнює:
υ = - Aw sin (w t + j) . (2)
В початковий момент часу t = 0 величини х і υ відповідно дорівнюють х0 і υ0:
x0 = A cos j i υ0 = - Aw sin j (3)
Розв’язавши систему рівнянь (3), одержимо значення амплітуди коливань і початкової фази:
= 1 , звідки А = 
;
cos j = 
, звідки j = arc cos 
.
Числові значення амплітуди і початкової фази в одиницях умови задачі
A = 
= 35,5 cм
j = arc cos 
.
Скориставшись значеннями амплітуди коливань і початкової фази, знаходимо координату х і швидкість υ в момент часу t:
x = 35,5 cos (4 × 2,40 + p/4) = - 20,2 (см)
υ= - 35,5 × 4sin (4 × 2,40 + p/4) = 115,7 (см/с)
Відповідь: х = - 20,2 см; υ= 115,7 см/с.
Приклад 2. В результаті додавання двох гармонічних коливань однакового напрямку і близьких частот одержали результуюче рівняння:
x = A cos 2,1 t cos 50,0 t (см)
Визначити циклічні частоти коливань, які додаються, і період биття.
Розв’язування: Відомо, що при додаванні двох гармонічних коливань з близькими частотами w1 і w2 рівняння результуючого руху має вигляд:
х = 
.
Порівнюючи це рівняння і рівняння умови задачі, маємо
= 2,1 c-1 i 
= 50,0 c-1
Звідки w1 = 47,9 c-1; w2 = 52,1 c-1.
Періодичність зміни амплітуди 
визначається періодичністю зміни модуля косинуса:
Tб = p ,
де Тб - період биття.
Знаходимо період биття
Tб = 
= 1,49 (с)
Відповідь:w1 = 47,9 с-1; w2 = 52,1 с-1; Тб = 1,49 с.
Приклад 3. Рівняння руху частинки мають вигляд:
х = Аsin wt; (1) y = В cos wt, (2)
де А і В - амплітуди коливань частинки вздовж координатних осей х і y. Знайти:
а) рівняння траєкторії частинки у(х) і напрям її руху вздовж цієї траєкторії;
б) прискорення а в залежності від напряму радіуса вектора 
.
Розв’язування: 
Рівняння траєкторії частинки одержимо, якщо рівняння (1) і (2) записати в такому вигляді:
sin wt = 
, cos wt = 
.
Піднесемо до квадрату:
= sin2wt; 
= cos2 wt;
Додавши ці рівняння одержимо:
+ = 1 - еліпс
Будуємо цю траєкторію в декартовій системі координат (рис.1):
Рис. 1
Аналізуючи рівняння (1) і (2) в різні моменти часу, знаходимо, напрям руху частинки вздовж траєкторії
а) при t = 0, х = 0 і у = В - початок руху ;
б) при t = p/4, х = А і у = 0 - наступна точка;
в) при t = T/2, х = 0 і у = -В і т.п.
Результуюче прискорення руху частинки визначаємо із відповідних прискорень руху вздовж осей х і у
υх = А wсos wt; ах= - А w2 sin wt = - w2 x;
υy = - В w sin wt; ay= - Вw2 cos wt = - w2 y;
.
Модуль вектора 
дорівнює
a = w2 
= w2 r ,
де - модуль радіуса-вектора частинки в довільний момент часу.
Радіус-вектор частинки завжди направлений від початку координат до положення точки на траєкторії. Вектор результуючого прискорення завжди направлений від положення частинки на траєкторії руху до початку координат, тобто
.
ПРИКЛАД 4. Однорідний стержень поклали на два блоки, які швидко обертаються, як це показано на рис.2. Відстань між осями блоків l = 20 см, коефіцієнт тертя ковзання між стержнем і блоками k = 0,18. Показати, що стержень буде здійснювати гармонічні коливання. Знайти період цих коливань.
| Дано: l = 20 см k = 0,18 ----------------- Т - ? |
Рис.2
|
Розв’язування: При зміщенні стержня вліво на величину х від положення рівноваги сили тертя F1 i F2, які виникають між стержнем і блоками дорівнюють
F1 = 
F2 = 
де r - густина матеріалу стержня;
S - переріз стержня;
k - коефіцієнт тертя ковзання.
Повертаюча сила, яка виникне в цьому випадку, буде дорівнювати:
F = - (F1 -F2) = - 2 r g S k x (1)
За другим законом Ньютона ця ж сила дорівнює:
F = m a (2)
Порівнюючи праві частини рівностей (1) і (2), маємо
ma + 2 r g S k x = 0,
aбо
x = 0 . (3)
Одержане диференціальне рівняння (3) є рівнянням гармонічних коливань. Циклічна частота цих коливань визначається співвідношенням:
w2 = 
,
звідки
T = 2p 
,
або врахувавши, що m = rlS, одержимо:
T = 2p 
.
Підставимо числові значення:
T = 6,28 × 
= 1,5 (c) .
Відповідь: Т = 1,5 с.
Приклад 5. Фізичний маятник у вигляді тонкого прямого стрижня довжиною 120 см коливається біля горизонтальної oсі, яка проходить перпендикулярно до стрижня через точку, віддалену на деяку відстань а від центра мас стрижня. При якому значенні ае період коливань буде мати найменше значення? Знайти величину цього періоду ?
Дано:
|
l = 120 см
-----------------
аe - ?
Тmin - ?
Розв’язування: Відведений від положення рівноваги стрижень буде здійснювати коливання відносно закріпленої осі, яка співпадає з віссю Z (рис.3). Покажемо, що при малих кутах відхилення (j < 7°), ці коливання будуть гармонічними. В будь-який момент часу на стрижень діють дві сили, сила тяжіння 
і сила реакції опори. Однак, обертаючий момент створюється лише силою тяжіння.
M =- mga sin j, (1)
де а - відстань від осі обертання до центра мас стрижня;
j - кут відхилення стрижня від положення рівноваги.
Для малих кутів sinj = j , а напрям вектора 
протилежний до напрямку осі Z, тому
Mz = - mga j, (2)
Згідно з основним рівнянням динаміки обертального руху цей момент дорівнює:
Mz = І 
(3)
Прирівняємо праві частини рівностей (2) і (3), одержимо:
I 
+ mga j = 0
Звідки:
j = 0. (4)
Рівняння (4) є диференціальним рівнянням гармонічних коливань, квадрат циклічної частоти яких дорівнює:
w2 = 
(5)
де І - момент інерції стрижня відносно осі обертання;
а - відстань від точки підвісу до центра мас.
Момент інерції стрижня знайдемо за теоремою Штейнера, згідно з якою:
I = I0 + m a2,
де І0 = 
ml2 - момент інерції стрижня відносно осі, яка проходить через центр мас стрижня. Тому
І = 
m l2 + ma2 . (6)
Підставимо (6) в (5) і визначимо період коливань
T = 2p 
. (7)
Для визначення екстремальної відстані ае від центра мас до точки підвісу, похідну по а підкореневого виразу формули (7) прирівняємо до нуля:
= 0 , 
.
Звідки
2 a2 - 
- a2 = 0;
ae = ± 
. (8)
ae = ± 0,34 (м).
Величину ае з (8) підставимо в (7) і знайдемо значення найменшого періоду коливань фізичного маятника:
Tmin = 2p 
= 1,67 (c).
Відповідь: ае = 34 см; Тmin = 1,67 c.
Приклад 6. Кулька масою m і радіусом r котиться без ковзання по внутрішній поверхні циліндра радіусом R, виконуючи малі коливання біля положення рівноваги. Визначити період коливань кульки.
|
Розв’язування: На відведену від положення рівноваги кульку діють дві сили, сила тяжіння mg і сила реакції опори з точкою прикладання о1. Обертаючий момент відносно миттєвої точки о1 створюється лише силою тяжіння (рис.4.):
М = - mgr sin a (1)
де mg - сила тяжіння;
r - радіус кульки;
a - кут відхилення радіуса - вектора кульки від положення рівноваги.
У випадку, коли кут a < 7°, sin a = a. В цьому випадку
M = - mgra (2)
За основним рівнянням динаміки обертального руху момент сили тяжіння дорівнює
М = І b, (3)
де І - момент інерції кульки відносно миттєвої вісі, яка проходить через точку о1 ;
b - кутове прискорення кульки відносно точки о1.
Прирівняємо праві частини рівностей (2) і (3):
I b + mgr a = 0 (4)
Момент інерції кульки відносно миттєвої осі знаходимо за теоремою Штейнера:
I = 
mr2 + mr2 = 
mr2 (5)
Кутове прискорення кульки b можна визначити через дотичне прискорення аt і радіус кульки r:
at = b r . (6)
Дотичне прискорення аt також можна визначити по відношенню до точки о циліндра:
at = e (R - r) , (7)
де e - кутове прискорення кульки відносно точки о, яке пов’язане із зміною кута повороту a за часом (e = a );
(R - r) - відстань від точки о до центра мас кульки.
Прирівняємо праві частини рівностей (6) і (7) і визначимо b:
b = 
. (8)
Значення І з (5) і b з (8) підставимо в (4), одержимо:
+ mgr a = 0.
Звідки
= 0. (9)
Диференціальне рівняння (9) є рівнянням гармонічних коливань. Циклічна частота цих коливань дорівнює
w = 
.
Отже період коливань кульки:
T = 2p 
.
Приклад 7. Тіло масою 1 кг знаходиться у в’язкому середовищі з коефіцієнтом опору r = 0,05 кг/с. З допомогою двох однакових пружин жорсткістю k = 50 Н/м кожна тіло утримується в положенні рівноваги, пружини при цьому не деформовані. Тіло змістили від положення рівноваги, як це показано на рис.5, і відпустили. Визначити: 1) коефіцієнт загасання b; 2) частоту n коливань; 3) логарифмічний декремент коливань δ; 4) число N коливань за час, протягом якого амплітуда коливань зменшиться в е разів; 5) добротність коливної системи.
|
m = 1 кг
r = 0,05 кг/с
k = 50 Н/м
--------------------------
b - ? n - ? δ - ?
N - ? q - ?
|
Аналіз задачі. На відведене від положення рівноваги тіло (рис.5) діють дві однакові сили F1 = F2 = kx, які направлені в один бік. Повертаюча сила в цьому випадку дорівнює:
Fn = - 2kx. (1)
При русі тіла у в’язкому середовищі з боку останнього виникає сила опору, яка пропорційна швидкості руху тіла:
F0 = - r 
. (2)
Інших сил в напрямі руху тіла при здійсненні коливань не існує. За другим законом Ньютона результуюча цих двох сил призводить до виникнення прискорення, тобто можна записати:
m 
= - r 
. (3)
Рівняння (3) можна перетворити:
= 0, (4)
де 
= 2b, b - коефіцієнт загасання;
= w02, w0 - власна циклічна частота.
З урахуванням позначень рівняння (4) набуде вигляду:
= 0. (5)
Рівняння (5) є диференціальним рівнянням загасаючих коливань, розв’язком якого є функція:
x = A0 e-bt cos (wt + j) (6)
Розв’язування: а) Коефіцієнт загасання дорівнює
b = 
= 0,025 c-1.
б) Частоту коливань n знайдемо за формулою:
n = 
= 1,59 c-1.
в) Логарифмічний декремент загасання дорівнює
δ = ln 
= 0,0157.
г) Число коливань, які будуть виконані коливною системою за час t, протягом якого амплітуда зменшиться в е разів:
N = 
,
де t - час, за який амплітуда зменшується в e paзів;
Т - період загасаючих коливань.
Спочатку знайдемо час t
1 = ln 
= b t
Звідки
t = 
.
Тоді
N = 
д) Добротність коливної системи
= 200.
Відповідь: n = 1,59 с-1; δ= 0,0157; N = 64; q = 200.
Приклад 8. Частинку змістили від положення рівноваги на відстань А0 = 1 см і відпустили. Який шлях пройде ця частинка, здійснюючи загасаючі коливання, до повної зупинки, якщо логарифмічний декремент загасання δ = 0.01 ?
Розв’язування: Зміщена від положення рівноваги частинка за перші чверть періоду, після того, як її відпустили, пройде шлях S1 = A0. За кожну наступну половину періоду частинка буде проходити відповідно шляхи
S2 =2A0 
; S3 = 2A0 
; S4 = 2 A0 × 
i т.п.
Весь шлях руху частинки буде дорівнювати
S = S1 + S2 + S3 +....+ Sn.
Або
S = А0 + 2А0 
+ 2А0 
+ 2А0 
+...+ 2А0 
.
Після спрощення одержимо
S = A0 × 
.
В круглих дужках безмежно спадна геометрична прогресія, сума членів якої визначається формулою
Sn = 
,
де а1 = 
- перший член геометричної прогресії; q = 
- знаменник прогресії.
Тому
S = A0 × 
.
Врахувавши те, що bТ =δ, одержимо
S = 0,01 × 
= 4 (м)
Відповідь: S = 4 м.
Приклад 9. До спіральної пружини жорсткістю 10 Н/м підвісили тягарець масою 10 г і занурили всю систему у в’язке середовище. Прийнявши коефіцієнт опору середовища рівним 0,1 кг/с, визначити: а) частоту n0 власних коливань; б) резонансну частоту nрез; в) резонансну амплітуду Арез, якщо змушуюча сила змінюється за гармонічним законом і її амплітудне значення F0 = 0,02 Н; г) відношення резонансної амплітуди до статичного зміщення пiд дією сили F0.
Аналіз теорії задачі.
На тягарець, який здійснює коливання, окрім сили тертя і пружної сили, діє зовнішня сила, яка змінюється за гармонічним законом.
З урахуванням дії всіх сил диференціальне рівняння коливань матиме вигляд:
m + r 
+ kx = F0 cos w t (1)
Поділимо рівняння (1) на масу тягарця m і введемо позначення:
; 
; 
, одержимо
+ 2b × + w02 x = f cos wt (2)
Рівняння (2) є неоднорідним лінійним диференціальним рівнянням другого порядку. Рoзв’язком такого рівняння є функція, яка складається з двох частин:
x = A0e-bt cos(wt + j) + A cos (wt + j) . (3)
Через деякий час під дією змушуючої сили коливання тягарця стануть стабільними. Тому розв’язком рівняння (2) буде лише функція
x = A cos (wt + j). (4)
Першу та другу похідні від (4) підставимо в (2):
= - Aw sin (wt + j) = Awcos (wt + j + p/2),
= - Aw2 cos (wt + j) = Aw2 cos (wt + j + p) ,
Aw2 cos (wt + j + p) + 2 b Aw cos (wt + j + p/2) +
+ Aw2 cos (wt + j) = f0 cos wt (5).
Введемо позначення: А1 = Aw2; A2 = 2 b Aw; A3 = A w02; A4=f0.
Для знаходження амплітуди А вимушених коливань скористаємось векторною діаграмою, на якій відкладемо амплітуди А1, А2, А3, А4 згідно з (5) (рис.6)
|
A42 = A22 + (A3 - A1)2, або врахувавши позначення, одержимо:
f02 = 4b2 A2 w2 + (w02 - w2) A2
Звідки маємо:
A = 
. (6)
Аналіз виразу (6) амплітуди вимушених коливань:
а) w << w0, тобто w ® 0
Aст = 
, (7)
де Аст - статичне зміщення тягарця під дією сталої сили F0.
б) w » w0
Aр = 
, (8)
де Ар - резонансне значення амплітуди.
При b ® 0, Аp ® ¥.
Для знаходження резонансної частоти і резонансної амплітуди дослідимо на максимум підкореневий вираз формули (6):
= 0 .
Звідки
wр = 
, (9)
де wр - резонансна частота вимушених коливань.
Значення wр з (9) підставимо в (6)
Aр = 
. (10)
Якщо b ® 0, то Aр = 
, що співпадає з формулою (8).
Розв’язування:
а) Частота n0 власних коливань тягарця дорівнює
n0 = 
= 5,03 c-1.
б) Резонансна частота знаходиться за формулою (9)
nр = 
= 
4,91 c-1 .
в) Резонансну амплітуду знайдемо за формулою (10):
Aрез = 
= 6,4 × 10-3 (м).
г) Відношення резонансної амплітуди до статичного зміщення тягарця, тобто добротність коливної системи, дорівнює
=
= 
= 160 .
Відповідь: n0 = 5,03 с-1; nр = 4,91 с-1; Ар = 6,4 мм; q = 160.
Механічні хвилі
Основні формули
Рівняння плоскої хвилі
,
де Ux,t - зміщення точок пружного середовища від положення рівноваги на відстані x від джерела;
А - амплітудне зміщення цих точок;
- хвильове число;
l - довжина хвилі;
w - циклічна частота коливань.
Рівняння сферичної хвилі.
,
де r - радіус-вектор пружного середовища.
3. Зв`язок довжини хвилі з періодом коливань і частотою:
де υ - швидкість поширення хвиль в пружному середовищі;
Т - період коливань;
n - частота коливань.
4. Швидкість поширення хвиль (фазова швидкість хвильового руху):
а) поздовжня хвиля в твердому середовищі:
де Е- модуль Юнга;
r - густина твердого середовища.
б) поперечна хвиля в твердому середовищі:
,
де G - модуль зсуву;
r - густина твердого середовища.
в) повздовжня хвиля в рідкому середовищі:
,
де K - модуль об’ємної пружності рідини;
r - густина рідини.
г) поздовжня хвиля в газоподібному середовищі:
υ = 
,
де g - стала Пуассона ( 
);
R - газова стала;
Т - абсолютна температура;
m - молярна маса газу.
5. Енергія пружних хвиль:
а) кінетична енергія
,
де m = rSDx - маса виділеного елемента пружного середовища;
- швидкість хвильового руху точок середовища.
б) потенціальна енергія
в) повна енергія хвиль
W = K + П = r S Dxw2 A2cos2 (wt - kx);
г) густина енергії
w = 
;
д) середні значення повної енергії і густини енергії за час в один період
, 
.
6. Потік енергії пружних хвиль
R = 
,
де 
- середнє значення повної енергії хвиль.
7. Вектор потоку енергії пружних хвиль
,
де 
- середня густина енергії пружних хвиль;
- вектор швидкості поширення хвиль в пружному середовищі.
8. Ефект Допплера для звукових хвиль
n ,
де n‘ - частота звуку яка сприймається приймачем;
n - частота звуку джерела;
с - швидкість поширення звукових хвиль в пружному середовищі;
υ - швидкість руху приймача звуку;
u- швидкість руху джерела звуку (нижній знак - джерело і приймач розходяться; верхній знак - джерело і приймач сходяться).
9. Інтерференція когерентних хвиль:
а) максимуми інтерференції спостерігаються, коли
Dj = 2p 
± 2n p,
де х2 - х1 - різниця ходів двох хвиль;
Dj - різниця фаз хвиль;
l - довжина хвилі;
n = 0, 1, 2, 3, ... - порядок max.
Або
Dx = (x2 - x1) = n × l;
б) мінімуми інтерференції спостерігаються, коли:
Dj = 2p 
.
або
Dx = (x2 - x1) = 
(2n + 1) l/2.
10. Рівняння стоячої хвилі
Ux,t = êA cos kxïcos wt ,
де Ux,t - зміщення точок середовища від положення рівноваги на відстані х від джерела коливань;
А - амплітуда зміщення;
k = 
- хвильове число;
w - циклічна частота коливань;
ïAcoskx ê - амплітуда стоячої хвилі.
а) Координати вузлів стоячої хвилі
kx = ± (2n + 1)p/2 , або x = ± (2n + 1)l/4 ,
де n = 0, 1, 2, 3, ...;
х - координати вузлів стоячої хвилі.
б) Координати пучностей стоячої хвилі
kx = ± np або x = ± n l
де n = 0, 1, 2, 3, .... .