Способ построения таблицы истинности для формул логики высказывания.
Логика высказываний– это определенная совокупность формул, т.е. сложных высказываний, записанных на специально сконструированном искусственном языке. Язык логики высказываний включает:
1. Неограниченное множество переменных: А, В, С, ..., А1, В1, С1, ..., представляющих высказывания;
2. Особые символы для логических связок: & – «и»; л – «или»; Л – «либо, либо»; → – «если, то»; ↔ – «если и только если»; ~ – «неверно, что» .
3. Скобки, играющие роль знаков препинания
Пример: «Сейчас день» - А, «Сейчас светло» - В; «Сейчас холодно» - С
"Если сейчас день, то сейчас светло или холодно":
А → В лС, или (А → (В л С))
"Если сейчас светло и холодно, то сейчас день":
В & С → А, или ((В & С) → А)
"Если неверно, что сейчас светло, то неверно, что сейчас день":
~ В → ~ А, или ((~ В) → (~ А))
Логика высказываний исходит из следующих двух допущений:
1. Всякое высказывание является либо истинным, либо ложным (принцип двузначности)
2. Истинное значение сложного высказывания зависит только от истинностных значений входящих в него простых высказываний и характера их связи.
Табличные определения союзов:
1. Конъюнкция (и - л) истинна, когда оба входящих в нее высказывания истинны;
2. дизъюнкция (или - v) истинна, когда хотя бы одно из входящих в нее
высказываний истинно;
3. Строгая дизъюнкция (или - ) истинна, когда одно из входящих в нее
высказываний истинно, а второе ложно;
4. Импликация (если.. то - →) истинна в трех случаях: ее основание и следствие истинны; основание ложно, а следствие истинно; и основание, и следствие ложны;
5. Эквивалентность (если и только если - ↔) истинна, когда два приравниваемых в ней
высказывания оба истинны или оба ложны;
6. Отрицательное высказывание истинно, когда отрицаемое высказывание ложно, и наоборот.
С помощью таблиц истинности в случае любого сложного высказывания можно определить, при каких значениях истинности входящих в него простых высказываний это высказывание истинно, а при каких ложно.
Истинная формула логики высказываний (тавтология) — это формула, дающая истинное высказывание при любых подстановках в нее конкретных (т.е. истинных или ложных) высказываний.
Ложная формула (логическое противоречие) всегда превращается в ложное высказывание при подстановке конкретных высказываний вместо ее переменных.
22.Выводы из категорических суждений: умозаключения по логическому квадрату, обращение и превращение.
Суждение– это форма мышления, в которой что–либо утверждается или отрицается в отношении существования предметов, связей между предметом и его свойствами или между предметами.
Суждения делятся на простые и сложные. Простым называется суждение, выражающее связь двух понятий. Суждение, состоящее из нескольких простых суждений, называется сложным.
Способы преобразования суждений:
Обращение – это преобразование суждения путем взаимного перемещения терминов без изменения качества связки.
Превращение– это такое преобразование суждения, когда изменяется его качество (характер связки) без изменения смысла и количественной характеристики.
«Логический квадрат». Вершины квадрата символизируют простые категорические суждения (А - общеутвердительное, Е - общеотрицательное, I – частноутвердительное, О – частноотрицательное), стороны и диагонали – логические отношения между суждениями.
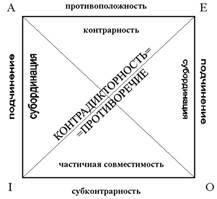
Совместимые суждения – это такие суждения, которые выражают одну и ту же мысль полностью или лишь в некоторой части.
В зависимости от степени совпадения мысли отношения совместимости могут быть в виде эквивалентности, логического подчинения, частичного совпадения (субконтрарности).
Эквивалентные суждения выражают одну и ту же мысль в различной форме.
Следует учитывать, что отношения между простыми эквивалентными суждениями с помощью логического квадрата не иллюстрируются.
Логическое подчинениеимеет общий предикат, а понятия, выражающие субъекты двух таких суждений, находятся в отношении логического подчинения. В данном случае одно суждение будет подчиняющим, а другое — подчиненным.
Частичное совпадение (субконтрарность) — отношение, в котором находятся два частных суждения — «I» и «О», имеющие одинаковые предикаты, но различающиеся по качеству. Эти суждения выражают противоположную мысль.
Несовместимыми называются суждения, которые одновременно не могут быть истинными. Виды:
1. Противоположными называются суждения, выражающие противоположные мысли.
2. Противоречащими называются суждения, исключающие друг друга.
Пользуясь правилами отношений между суждениями, по логическому квадрату можно получить выводное знание, обеспечив правильность мысли.
23.Выводы из категорических суждений: противопоставление предикату и противопоставление субъекту.
Суждение– это форма мышления, в которой что–либо утверждается или отрицается в отношении существования предметов, связей между предметом и его свойствами или между предметами.
Суждения делятся на простые и сложные. Простым называется суждение, выражающее связь двух понятий. Суждение, состоящее из нескольких простых суждений, называется сложным.
Противопоставление предикату - логическую операцию, в результате которой субъектом становится понятие, противоречащее предикату, а предикатом – субъект исходного суждения.
Противопоставление предикату является сложной операцией, состоящей из двух других - превращения, а затем обращения результата превращения.
Обращение – это преобразование суждения путем взаимного перемещения терминов без изменения качества связки.
Превращение– это такое преобразование суждения, когда изменяется его качество (характер связки) без изменения смысла и количественной характеристики.