Различные определения вероятности случайного события
Элементы теории вероятностей
Cлучайные события и операции над ними.
Различные определения вероятности случайного события
Случайными событиями называются такие события, которые в результате опыта могут произойти или не произойти. Случайные события обозначают большими латинскими буквами А, В, С, … , U, V.
Событие называется достоверным, если оно обязательно появляется в результате данного опыта, и невозможным, если оно не может появиться в условиях данного опыта. Примером достоверного события может, например, служить вынимание белого шара из ящика, в котором находятся лишь белые шары, а невозможного – выпадение цифры 7 при бросании игральной кости. Достоверное событие будем обозначать символом U, невозможное – символом О.
Если события А и В не могут произойти одновременно, то их называют несовместными, а если события А и В могут произойти одновременно, то они называются совместными.
События равновозможны, если ни одно из них не является более возможным по сравнению с другим, то есть не имеет больше шансов для появления.
События А1, А2, …, Аk образуют полную группу, если они попарно несовместны и их сумма является достоверным событием:А1 + А2 + … + Аk = U.
Вероятность события А определяется равенством
P(A) = 
,
где n – общее число всех возможных элементарных исходов опыта, а m – число элементарных исходов, благоприятствующих появлению события А.
Под элементарными исходами опыта понимают события, которые появляются как результат опыта и удовлетворяют следующим свойствам: они несовместны, равновозможны и единственно возможны в данных условиях.
Приведенное определение вероятности случайного события носит название классического. Существуют еще два подхода к понятию вероятности, которые приводят к определению статистической вероятности и геометрической вероятности. Рассмотрим сначала первый из них.
Пусть некоторый опыт повторяется n раз, при этом в m испытаниях наступает событие А. Отношение , то есть числа испытаний (исходов), в которых наступило событие А, к общему числу произведенных испытаний (экспериментов) называют относительной частотой события А в данной серии испытаний. Относительную частоту события А называют еще эмпирической вероятностью.
При многократно повторяющихся опытах относительная частота имеет тенденцию стабилизироваться около некоторой постоянной величины. Иначе говоря, если число испытаний n неограниченно увеличивать, то меняется и число m испытаний, в которых наступает событие А, но отношение при этом приближается сколь угодно близко к некоторому числу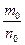 
, которое и называется статистической вероятностью события.
Заметим, что статистическую вероятность события невозможно подсчитать заранее, не проводя эксперимента. Даже определение эмпирической вероятности требует действительного проведения опыта и повторения его достаточно много раз. При использовании классического определения не требуется, чтобы испытания практически осуществлялись.
В практике встречаются события, вычислить вероятности которых с помощью классического или статистического определений не удается. Такие ситуации возникают в случаях, когда число различных исходов испытания бесконечно. Пусть, например, множество всех исходов есть множество точек отрезка b на прямой. Отрезок а составляет часть отрезка 
. Наугад на отрезок b бросается точка, то есть она случайным образом на отрезке указывается. Предполагается при этом, что все исходы этого эксперимента равновозможны, т. е. все точки отрезка b равноправны. Тогда вероятность события А – “точка попадет на отрезок а” определяется равенством:
.
Данное отношение и выражает собой геометрическое определение вероятности..
Для фигур, расположенных в плоскости или в пространстве, вероятность попадания точки на меньшую фигуру, являющуюся частью большей, выражается отношением площадей, соответственно объемов этих фигур.
Подводя итог различным определениям вероятности, можно сформулировать требования, которым должно удовлетворять любое математическое определение вероятности. Во-первых, вероятностью должна быть величина, которую можно вычислить для любого случайного события, не производя опытов, а во-вторых, для нее должны выполняться следующие основные свойства.
Свойства вероятности.
1. 0 £ Р(А) £ 1 для любого события А.
2. Вероятность достоверного события равна 1;
3. Вероятность невозможного события равна 0.
Задачи
1. Для рассмотрения уголовного дела должен быть назначен один из пяти судей. Известно, что трое из них берут взятки. Какова вероятность того, что дело будет вести честный судья?
2. В урне имеется 10 шаров: 3 белых и 7 черных. Из урны наугад вынимается один шар. Какова вероятность, того, что этот шар: а) белый; б) черный?
3. В программе экзамена по уголовному праву 40 билетов. Билеты с 1 по 8 и с 14 по 18 считаются «хорошими». Найти вероятность не вытащить «хороший билет».
4. Одновременно бросают две монеты. Найти вероятность того, что:
а) герб выпадет два раза,
б) монеты выпадут разными сторонами,
в) герб не выпадет ни разу,
г) выпадет хотя бы один герб?
5. В лотерее разыгрывается 1000 билетов. Из них в одном билете достается выигрыш в 5000 рублей, в десяти — 1000 рублей, в пятидесяти — двести рублей, в ста достается пятьдесят рублей. Остальные билеты без выигрыша. Некто покупает один билет. Найти вероятность выигрыша им не менее двухсот рублей.
6. При броске игральной кости вычислите вероятности следующих событий:
а) «выпало 2 очка»,
б) «выпало 8 очков»,
в) «выпало четное число очков»,
г) «выпало простое число очков»,
д) «число выпавших очков кратно 3».
7. Дважды подбрасывается игральная кость. Какова вероятность того, что:
а) при первом бросании выпала цифра 6,
б) в первый раз выпала цифра 2, а во второй раз – 5,
в) в сумме выпало 5 очков,
г) оба раза выпало четное число очков?
8. Во время процедуры опознания на скамью посадили двух подозреваемых вместе с четырьмя другими лицами. Какова вероятность того, что на скамье между подозреваемыми оказалось: а) два человека, б) три человека.
9. Преступник знает, что шифр сейфа составлен из цифр 1, 2, 6, 7 и что цифры в нем не повторяются, но не знает, в каком порядке их набирать.
1) Какова вероятность того, что первые две цифры он набрал верно?
2) Какова вероятность, что преступник откроет сейф с первой попытки?
10. Один раз бросаются две игральные кости. Найдите вероятности следующих событий:
1) Сумма выпавших очков равна 2, 3, …, 12. Полученные результаты изобразите на координатной плоскости точками, у которых абсцисса равна сумме очков, а ордината — вероятности этой суммы.
2) Разность выпавших очков равна 0, 1, 2, 3, 4, 5.Какие события окажутся наиболее (наименее) вероятными?
Решение.
Общее число возможных исходов при бросании двух игральных костей равно 6×6 = 36.
1) Пусть событие А – сумма выпавших очков равна 2, тогда Р(А) = 
. Событие В – суммавыпавших очков равна 3, тогда Р(В) = 
. Событие С – сумма очков равна 4, тогда Р(С) = 
. Событие D – сумма равна 5, тогда Р(D) = 
. Событие E – сумма очков равна 6, Р(E) = 
. Событие F – сумма выпавших очков равна 7, Р(F) = 
.
Событие G – сумма выпавших очков –8, 
Р(G) = .
Событие H – сумма очков – 9,
Р(H) = .
Событие K – сумма очков равна 10,
Р(K) = .
Событие L – сумма выпавших очков равна 11, Р(L) = .
Событие M – сумма выпавших очков равна 12, тогда Р(M) = .
2) Разность выпавших очков равна 0 в том и только том случае, если число очков выпавших на одной кости равно числу очков на другой. Исходов, благоприятствующих этому событию, всего шесть. Р(А) = .
Пусть А состоит в том, что разность между числами равна 1 (или -1). Перечислим исходы, благоприятствующие появлению события А:
(1, 2), (2, 1), (2, 3), (3, 2), (3, 4), (4, 3), (5, 4), (4, 5), (5, 6), (6, 5).
Получаем m =10. Тогда Р(А) = 
= 
.
Событию В, состоящему в том, что разность между очками, выпавшими на двух костях, равна 2, благоприятны восемь исходов:
(1, 3), (3, 1), (2, 4), (4, 2), (3, 5), (5, 3), (4, 6), (6, 4).
Таким образом,
= 
= 
.
Разность между числами равна 3 для следующих пар:
(1, 4), (4, 1), (2, 5), (5, 2), (3, 6), (6, 3).
Значит, 
= .
Разность между числами равна 4 для пар: (1, 5), (5, 1), (2, 6), (6, 2).
Значит, 
= 
= .
Разность между числами равна 5 для пар: (1, 6), (6, 1).
Значит, 
= 
= .
Ответ. 1) , , , , , , , , , , ;
2) , , , , , .
11. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера. Полученные кубики тщательно перемешаны. Определить вероятность того, что кубик, извлеченный наудачу, будет иметь: а) одну окрашенную сторону, б) две окрашенные стороны, в) три окрашенные стороны.
Решение.
Всего кубиков n =1000.
У куба 6 граней, на каждой из которых лежат 64 кубика с одной окрашенной стороной. Значит всего таких кубиков (следовательно, и благоприятных исходов) будет 64×6 = 384.
= 0,384.
Куб имеет 12 ребер, на каждом из которых по 8 кубиков с двумя окрашенными сторонами. Поэтому m = 12×8 = 96.
= 
= 0,096.
Куб имеет 8 вершин, следовательно, 8 кубиков будут иметь три окрашенные стороны. Таким образом, m = 8. 
= 0,08.
Ответ. а) 0,384; б) 0,096; в) 0,08.
12. На электроламповом заводе относительная частота брака лампочек составила 0,004. Найти ожидаемое число годных лампочек в партии из 100000 штук.
13. Каждому пассажиру поезда вручается страховой полис на 30000 рублей при взимании с него 5 рублей. Какова средняя прибыль страховой компании от продажи 400000 билетов, если несчастные случаи происходят в среднем с одним пассажиром из 100000 человек? (Считать, что страховка выплачивается только в случае гибели пассажира).
Решение.
Относительная частота проезда пассажира без несчастного случая равна 1– 0,00001 = 0,99999. С такой частотой компания получает с пассажира 5 рублей, с частотой 0,00001 она выплачивает за одного пассажира 29 995 рублей (так как 5 рублей она с пассажира изъяла). Следовательно, ее ожидаемая прибыль с продажи одного билета составляет 
= 4,99995 – 0,29995 = 4,7 (руб). Тогда с продажи 400 000 билетов ожидаемая прибыль составит 1 880 000 рублей.
14.В урне 10 белых, 15 черных, 20 синих, и 25 красных шаров. Вынули один шар. Какова вероятность того, что вынутый шар 1) белый? 2) черный? 3) синий? 4) красный? 5) белый или черный? 6) синий или красный? 7) белый, или черный, или синий?
15.Имеются две концентрические окружности с радиусами5 и10 см., соответственно. Найти вероятность того, что точка, брошенная наугад в большой круг, попадет в кольцо, образованное окружностями.
16.Вокружность вписан квадрат . В круг, ограниченный этой окружностью, наудачу бросается точка. Какова вероятность, что она попадет в квадрат?
17. Вокружность вписан правильный треугольник. В круг, ограниченный этой окружностью, наудачу бросается точка. Какова вероятность, что она попадет в область, ограниченную треугольником?
18.В квадрат со стороной а вписана окружность. Найдите вероятность того, что точка, наудачу поставленная в квадрат, попадет в круг, ограниченный окружностью.
19.Двое договорились о встрече на следующих условиях: каждый приходит в указанное место независимо друг от друга и наудачу в любой момент времени от 13.00 до 14.00. Придя, ожидает не более получаса, а уходит не позднее 14.00. Какова вероятность того, что они встретятся?
20.Противотанковые мины поставлены на прямой через 15 метров. Танк шириной 3 метра идет перпендикулярно этой прямой. Какова вероятность, что он подорвется?