Наибольшего и наименьшего значений

Нижегородский государственный педагогический университет

Элементарная математика:

Элементарные функции

Методические рекомендации для студентов

Математического факультета

Нижний Новгород

Печатается по решению редакционно-издательского совета Нижегородского государственного педагогического университета

Элементарная математика: элементарные функции:Методические рекомендации для студентов математического факультета. Н. Новгород: НГПУ, 2006. с.

Авторы-составители: С.В. Кириллова, канд. пед. наук, доцент кафедры

теории и методики обучения математике НГПУ

О.К. Огурцова, канд. пед. наук, старший препода-

ватель кафедры теории и методики обучения

математике НГПУ

Рецензент: Л.И. Кузнецова, канд. пед. наук, доцент кафедры теории и

методики обучения математике НГПУ

Ответственный за выпуск: Т.А. Иванова, доктор пед. наук, профессор, зав.

каф. теории и методики обучения математике

НГПУ

Методические рекомендации содержат программу дисциплины «Элементарная математика: элементарные функции», планы практических занятий с выделением основных типов и методов решения задач, список рекомендуемой литературы, список задач к зачёту.

Предназначено для студентов очной формы обучения по специальности 032100.00 - «Математика с дополнительной специальностью».

Предисловие

Изучение элементарных функций является одной из главных задач школьной математики. Это объясняет необходимость детального и глубокого рассмотрения в педагогическом вузе данного вопроса. Сформировать все умения, определяемые содержанием школьного курса математики, в пределах только рассматриваемого курса не представляется возможным в виду ограниченности по времени. Поскольку многие умения формируются при изучении соответствующих разделов в специальных курсах высшей математики, то нет необходимости включать эти разделы в программу данной дисциплины. К числу таких относятся: определение понятия действительной функции действительного переменного, способы задания функции, арифметические действия над функциями, композиция функций, предел функции в конечной точке и на бесконечности, непрерывность функции в точке и на промежутке, понятие обратной функции, исследование функций с помощью производной и построение графиков на его основе.

Так как программой не отводится времени на лекции, то основные теоремы, необходимые для решения задач, приводятся на практических занятиях без доказательств. Заметим, что многие из них доказываются в курсе «Введение в анализ», который студенты изучают параллельно. Основные понятия курса «Элементарные функции» знакомы студентам из школьного курса математики. Здесь предполагается освещение вопросов с учётом профессиональных интересов будущего учителя, расширение, углубление и систематизация имеющихся знаний. Особое внимание уделяется выделению типов задач, решаемых на основе известных (и уточнённых) определений понятий и теорем, поиску способов и алгоритмов их решений, что требует от студентов знаний основных теоретических сведений о математических предложениях, их структуре, технологии построения отрицаний определений, умения подводить объект рассмотрения под известное определение понятия и выводить следствие из определения.

Общие цели изучения курса состоят в следующем:

- создание необходимой теоретической базы для решения задач;

- формирование первоначальных методических умений, связанных с решением задач;

- выделение основных типов задач, решаемых на основе изученного теоретического материала;

- выделение методов и приёмов решения задач основных типов;

- формирование умений применять выделенные приёмы и методы при решении задач.

Конкретные учебные задачи и диагностируемые цели сформулированы к каждому занятию.

Целью данных методических рекомендаций является оказание помощи студентам математического факультета в усвоении дисциплины «Элементарная математика: элементарные функции».

Методические материалы включают:

- тематический план учебной дисциплины;

- планы практических занятий;

- рекомендуемую литературу;

- список задач к зачёту.

Учебная дисциплина «Элементарная математика: элементарные функции» включена в цикл дисциплин общепрофессиональной подготовки студентов и читается в рамках вузовского компонента Государственного образовательного стандарта по специальности 032100.00- «Математика с дополнительной специальностью». Программа учебной дисциплины «Элементарная математика: элементарные функции» построена в соответствии с учебной программой дисциплины «Элементарная математика», разработанной Л.И. Кузнецовой (Н. Новгород: НГПУ, 2003), включённой в федеральный компонент ГОС. Дисциплина «Элементарная математика: элементарные функции» изучается в 1-м семестре и завершается зачётом.

I. Тематический план учебной дисциплины

«Элементарная математика: элементарные функции»

№ п/п	Темы практических занятий	Количество часов
1.	Определение и свойства функции. Нахождение области определения и множества значений функции, наибольшего и наименьшего значений.
2.	Исследование функции на чётность и нечётность, периодичность, монотонность элементарными средствами.
3.- 4.	Построение графиков функций с помощью преобразований графиков основных элементарных функций.
5.	Контрольная работа.
6.–7.	Построение графиков функций, содержащих модуль в аналитическом задании.
8.	Построение графиков сложных функций элементарными средствами.
	Всего:

Форма контроля:зачёт.

II. Планы практических занятий

Занятие № 1

Определение и свойства функции. Нахождение области определения и множества значений функции,

наибольшего и наименьшего значений

Учебная задача: формирование умений в нахождении области определения, множества значений, наибольшего и наименьшего значений функции элементарными средствами.

В результате студент:

Знает

- определение числовой функции;

- основные способы задания функции;

- определение графика функции;

- необходимое и достаточное условие того, чтобы кривая являлась графиком некоторой функции;

- понятие области определения функции;

- понятие множества значений функции;

- понятие наибольшего (наименьшего) значения функции;

- различные подходы к нахождению множества значений функции;

Имеет представление

- об основных свойствах функций;

- о построении графика функции на основе исследования ее свойств;

- об ограничениях, которые учитываются при нахождении области определения функции;

Умеет

- находить область определения при аналитическом и графическом задании функции;

- находить множество значений при аналитическом и графическом задании функции;

- находить наибольшее и наименьшее значения при аналитическом и графическом задании функции.

Содержание занятия:

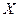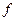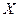Определение: Если даны числовое множество и правило , позволяющее поставить в соответствие каждому элементу из определённое число , то говорят, что задана функция с областью определения 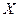. Переменную называют независимой переменной или аргументом, а переменную – зависимой переменной или функцией.

Существует 4 основных способа задания функции:

· аналитический;

· табличный;

· графический;

· словесный.

Определение: Графиком функции называется множество всех точек координатной плоскости, абсциссы которых есть значения независимой переменной, а ординаты – соответствующие им значения функции.

Для того чтобы кривая была графиком некоторой функции, необходимо и достаточно, чтобы всякая прямая, параллельная оси ординат, либо не пересекалась с этой кривой, либо пересекала её в единственной точке.

Существуют различные способы построения графиков функций. Универсальным можно считать способ, основанный на исследовании основных свойств функции:

· область определения;

· множество значений;

· чётность, нечётность;

· периодичность;

· монотонность.

Область определения функции есть множество всех допустимых значений независимой переменной . Обозначение: или .

Если функция задана аналитически, то под областью определения этой функции следует понимать множество всех значений аргумента, при которых выполнимы все действия, указанные в формуле. Область определения функции находится с учетом следующих ограничений:

- на ноль делить нельзя;

- корень чётной степени можно извлекать только из неотрицательных чисел;

- степень с действительным показателем определена только для положительного основания;

- отрицательные числа и ноль логарифма не имеют;

- тангенс существует для всех чисел, кроме чисел , где ;

- котангенс существует для всех чисел, кроме чисел , где ;

- арксинус и арккосинус определены только для чисел из отрезка .

Пример 1. Найдите область определения функции .

Решение: Область определения функции есть множество значений . В данном примере отыскание области определения сводится к решению неравенства . Имеем . Учитывая тот факт, что квадратный корень можно извлекать только из неотрицательных чисел, переходим к следующему двойному неравенству: . Получаем

Применив метод интервалов для решения неравенств, находим: .

Ответ: .

При графическом задании функции область определения – проекция графика на ось абсцисс.

Множество значений функции есть множество всех возможных значений зависимой переменной. Обозначение: или .

Если функция задана аналитически, то под множеством значений этой функции следует понимать множество всех значений , при которых уравнение имеет решение относительно , принадлежащих области определения функции.

Пример 2.Найдите множество значений функции .

Решение: Область определения заданной функции есть всё множество действительных чисел. Для отыскания множества значений функции рассмотрим, при каких значениях у уравнение имеет решение относительно ÎR. Квадратное уравнение имеет решение тогда и только тогда, когда его дискриминант неотрицателен. Получаем , т.е. .

Ответ: .

Возможен другой подход к нахождению множества значений функции. Он основан на том факте, что если функция получена из некоторой элементарной функции умножением на число, сложением с числом, возведением в степень, извлечением корня, то множество значений заданной функции можно получить из множества значений элементарной функции с помощью свойств неравенств.

Таким образом, в примере 2, выделив полный квадрат, запишем данную функцию в виде . Множество значений функции есть множество всех неотрицательных чисел, так как эта функция получена из функции , принимающей все возможные действительные значения, возведением в чётную степень. Переходим от верного неравенства к неравенству , т.е. .

Пример 3. Найдите множество значений функции.

Решение: В указанном виде функция представляет собой комбинацию двух элементарных функций: и .Однако данная функция легко приводится к одной элементарной функции:

где определяется из равенств , .

Теперь можно использовать свойства неравенств:

Ответ: .

Иногда множество значений функции легко находится, если предварительно найти область определения функции.

Пример 4. Найдите множество значений функции.

Решение: Найдём сначала область определения функции:

, значит . Так как , то в заданной функции может принимать только значение при , . Тогда множество значений функции состоит из одного числа .

Ответ: .

При графическом задании функции множество значений – проекция графика на ось ординат.

Существуют и другие способы нахождения множества значений функции.

Заметим, что, находя множество значений функции, мы одновременно находим и её наибольшее и наименьшее значения, если они существуют. Так при графическом задании функции наибольшее и наименьшее значения функции есть соответственно наибольшее и наименьшее значения из множества проекций.

Число называют наименьшим значениемфункции на множестве , если:

1) в 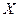существует такая точка , что ;

2) для всех из 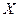выполняется неравенство .

Число называют наибольшим значениемфункции на множестве , если:

1) в Х существует такая точка , что ;

2) для всех из 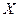выполняется неравенство .

В примере 2 функция имеет только наименьшее значение: у_наим. = 3. В примере 3 , .

Пример 5. Найдите наибольшее и наименьшее значения функции

Решение: Приведём данную функцию к одной элементарной функции: . Множество значений функции есть отрезок , поэтому выражение принимает все значения из отрезка . Тогда выражение принимает все значения из отрезка , а выражение – все значения из отрезка . Потому множеством значений заданной функции является отрезок . Тогда – наименьшее, - наибольшее значения функции.

Ответ: , .

Упражнения к занятию:

1. Почему постоянную величину можно рассматривать как функцию некоторого аргумента?

2. Даны две функции: и . Как записать, что значение при равно значению при ?

3. Дана функция . Как записать, что: 1) число является корнем данной функции; 2) при противоположных значениях аргумента функция принимает: а) равные значения; б) противоположные значения?