ТЕМА 17. СПЛАВЫ И ДИАГРАММЫ ПЛАВКОСТИ.
Пример 1. Определение числа степеней свободы в гетерогенной равновесной системе.
Найдите число степеней свободы в системе свинец-висмут, если из расплава Pb–Bi будут выпадать кристаллы Bi.
Решение. Под числом степеней свободы в равновесной гетерогенной системе понимают условия (температуру, давление, концентрацию веществ),которые можно произвольно изменять, не нарушая равновесия системы и не изменяя числа фаз в системе. Число степеней свободы С в равновесной гетерогенной системе рассчитывается при помощи правила фаз: С = К – Ф + 2, где К – число независимых компонентов системы; Ф – число фаз в системе. Для систем состоящих только из твердых и жидких фаз, давление не учитывается, и правило фаз имеет вид: С = К – Ф + 1. В данной системе число независимых компонентов – 2 (свинец и висмут), две фазы – расплав и кристаллы висмута. Число степеней свободы в этой гетерогенной системе: С = 2 – 2 + 1 = 1. Эта система имеет одну степень свободы, поэтому до известного предела можно изменять температуру или концентрацию компонентов системы, не нарушая равновесия системы.
Пример 2. Вычисление процентного состава эвтектики.
Сплав содержит 30% Pb и 70% Sb. В 800 г сплава содержится 524 г свинца в виде кристаллов, вкрапленных в эвтектику. Рассчитайте состав эвтектики.
|
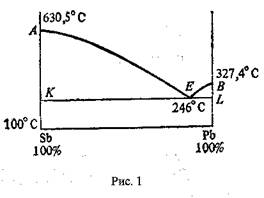
Решение. Эвтектика – механическая неоднородная смесь, состоящая из мелких кристаллов двух компонентов сплава, образовавшаяся в результате одновременной кристаллизации обоих компонентов. Эвтектическому сплаву Sb – Pb отвечает следующая диаграмма плавкости (рис. 1). Над линией АЕВ – область жидкого раствора; точка А – температура плавления чистой сурьмы; В – температура плавления чистого свинца; область КАЕ – жидкий сплав с кристаллами сурьмы; область ВЕL – жидкий сплав с кристаллами свинца; Е (t=246°C) – точка кристаллизации эвтектики. Этот сплав имеет самую низкую температуру кристаллизации. Ниже линии KEL сплав находится в твердом состоянии.
Находим массу каждого металла, содержащуюся в 800 г сплава:
m(Pb) = 800·0,3 = 240 г; m(Sb) = 800·0,7 =560 г.
Масса эвтектического сплава равна 800–524 = 276 г. Таким образом эвтектика содержит 240 г свинца и 36 г сурьмы. По массам сурьмы и свинца, содержащимся в эвтектическом сплаве, определяем состав эвтектики:
Pb = (240/276)·100% = 87%; Sb = (36/276)·100% = 13%.
Пример 3. Определение температуры затвердевания и плавкости сплавов, образующих твердые растворы.
Определите температуру затвердевания и плавления сплава, содержащего 25% серебра и 75% золота.
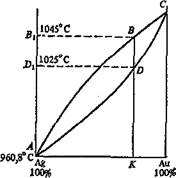
Решение. Твердые растворы образуют компоненты сплавов, неограниченно растворяющиеся друг в друге, как в жидком, так и в твердом состояниях и не образующие между собой при этом химических соединений. Серебро и золото образуют при сплавлении твердый раствор. Сплаву Ag –Au отвечает диаграмма плавкости (рис. 2). Кривая АВС отвечает температуре плавления сплавов; кривая ADC – температуре затвердевания сплавов. Точка К на оси абсцисс соответствует сплаву, содержащему 25% Ag и 75% Au. Из точки К проводим прямую параллельную оси ординат, до пересечения с кривой плавления и затвердевания в точках В и D. Из точек В и D проводим прямые, параллельные оси абсцисс, до пересечения с осью ординат в точках В1 и D1. Точка D1 соответствует температуре затвердевания сплава, которая равна 1025°С. Температура полного плавления сплава равна 1045°С (точка В1).
С
|
Рис. 2.
Пример 4. Определение состава твердой и жидкой фаз при заданной температуре.
Найдите состав жидкой и твердой фаз в системе, содержащей 60% свинца и 40% олова при 200°С. Какова масса твердой фазы, выделившейся при этой температуре из 5 кг сплава?
Решение. На диаграмме плавкости для сплава Pb – Sn (рис. 3) данному составу и данной температуре соответствует точка К, через которую проведем прямую, параллельную оси абсцисс, до пересечения с кривой АЕ и ординатой, соответствующей чистому Pb.

Точка F отвечает составу жидкой фазы, а точка N – твердой фазы. Жидкая фаза имеет состав: 55% олово, 45% свинец. Твердая фаза представляет собой чистый свинец. Массы твердой mт и жидкой mж фаз в сплаве данного состава при данной температуре определяют по «правилу рычага»: массы твердой и жидкой фаз обратно пропорциональны длинам отрезков между точкой, выражающей состояние данной системы, и точками, определяющими состав твердой и жидкой фаз: mт /mж = KF/NK. Общая масса сплава 5 кг, тогда mж = 5 – mт. Выразим длины отрезков: NK=40, KF = 15. Тогда mт/5 – mж = 15/40. Вычислим mт = 75/55 = 1,36 кг. Таким образом при 200°С на 5 кг сплава выделяется 1,36 кг свинца (твердой фазы).
Пример 5. Определение формулы интерметаллического соединения, образующегося при сплавлении металлов.
По диаграмме плавкости системы Pb — Мg определите формулу интерметаллического соединения, образуемого этими металлами, Какова масса химического соединения, содержащегося в 500 г сплава состава 40 % Pb и 60 % Мg?
Решение. Интерметаллическое соединение образуется в тех случаях, если компоненты данной системы химически взаимодействуют между собой и в жидком состоянии полностью растворимы друг в друге, а в твердом состоянии совершенно нерастворимы. Максимум на кривой АВСDМ (точка С) отвечает температуре плавления интерметаллического соединения, образованного магнием и свинцом (рис. 4).

Температура плавления интерметаллического соединения равна 551° С. Из диаграммы плавкости видно, что интерметаллическое соединение содержит 80 % Pb и 20 % Мg. Обозначим формулу интерметаллического соединения через МgxРbу, тогда
x : y = (20/24,305) : (80/207,29) = 0,82 : 0,39 = 2 : 1, где 24,305 и 207,29 — соответственно атомные массы Мg и Рb. Формула интерметаллического соединения: Мg2Рb. В сплаве Мg больше, чем в составе химического соединения. Свинец полностью входит в состав химического соединения. В 500 г сплава содержится 500∙0,4 = 200 г свинца. По массе свинца определяем массу химического соединения: 200 / 0,8 = 250 г.
316. Найдите число степеней свободы в системе свинец серебро, если из расплава Pb Аg одновременно выделяются кристаллы свинца и серебра.
Ответ: 0.
317. Из скольких фаз состоит сплав, содержащий 20 % Вi и 80 % Сd при 250 °С? Сколькими степенями свободы обладает эта система (см. диаграмму плавкости, рис. 5)? Ответ: 2 фазы; 1.
С

|
100%
Рис. 5
318. Сплав содержит 24 % Сd и 76 % Вi. В 1 кг сплава содержится 400 г кадмия в виде кристаллов, вкрапленных в эвтектику. Определите процентный состав эвтектики. Ответ: 40% Cd, 60% Bi.
319. Эвтектика сплава Аg — Сu имеет состав: 28 % Си и 72 % Аg. Какая масса эвтектики содержится в 750 г твердого сплава, если сплав содержит 63 % Си и 37 % Ag? Ответ: 385,4 г.
320. По диаграмме плавкости (рис. 6) найдите состав жидкой и твердой фаз в системе, содержащей 50 % Аg и 50 %Сu при 900 °С. Какая масса твердой фазы выделится из 1,5 кг сплава при этой температуре? Ответ: 0,41 кг.

|
Рис. 6.
321. По диаграмме плавкости сплава Вi — Рb (рис. 7) определите состав жидкой и твердой фаз для системы, содержащей 55 % Рb и 45 % Вi при 150 °С. Какая масса твердой фазы выделится при кристаллизации 300 г этого сплава при данной температуре? Ответ: 75 г.
322. Сколькими степенями свободы обладает система, содержащая 40 % Си и 60 % Аg (см. диаграмму плавкости задачи 707) при 800 °С? Ответ: 1.

323. Определите температуру затвердевания и плавления сплава, содержащего 60 % Ni и 40 % Сu (см. диаграмму плавкости, рис. 8).Ответ: 1230, 1370°С.

Рис. 8.
324. При какой температуре будет затвердевать и плавиться сплав, содержащий 80 % Аu и 20 % Рt? Определите число степеней свободы для сплава данного состава при 1200 °С (см. диаграмму плавкости, рис. 9). Ответ: 1150; 1300°С, 1.

Рис. 9.
325. По диаграмме плавкости системы Мg — Zn (рис. 10) определите формулу интерметаллического соединения, образуемого этими металлами. Какова масса химического соединения, содержащегося в 250 г сплава состава: 40 % Zn и 60 % Мg? Ответ: MgZn2; 120,5 г.

|
326. По диаграмме плавкости системы Ni — Sb (рис. 11) установите формулы интерметаллических соединений, образуемых при сплавлении этих металлов. Ответ: NI3Sb; NiSb.
 Рис. 11.
Рис. 11.
327. При сплавлении лантан и таллий образуют интерметаллическое соединение, имеющее состав: 42 % Т1 и 58 % La. Установите формулу этого соединения. Какой из металлов находится в свободном состоянии при охлаждении жидкого сплава, содержащего 30 % Т1 и 70 % La? Какая масса этого металла содержится в 750 г сплава? TlLa2; 214,3 г.