Поля напряжение и перемещений вблизи кончика трещины. Коэффициент интенсивности напряженй

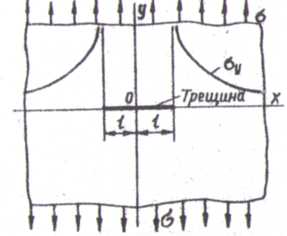Для анализа напряженного состояния в окрестности кончика тре­щины рассмотрим тонкую бесконечную пластинку, которая подвергает­ся равмерному растяжению в одном направлении (рис. 3). Пусть в этой пластинке имеется тонкая тре­щина (разрез) длиной 2t . Метода­ми теории упругости можно показать, что нормальное напряжение Ϭу в точках на сои х (при /х/ > t ) выражается формулой :

рис.3

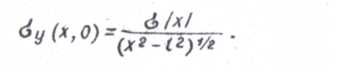(2)

Формулу (3) можно переписать так:

Эпюра напряжения Ϭу, подсчи­танного по формуле (2), показана на рис. 3. Напряжение Ϭу стре­мится к бесконечности при подходе к кончику трещины, т.е, имеет особенность в кончике. Для установления характера особенности нор­мального напряжения у кончика трещины найдем асимптотическое пред­ставление для Ϭу при х→t+0. Устремляя в формуле (2) X к t+0 , находим

(3)

 

где К1 - коэффициент интенсивности нормальных напряженй, завися­щий от внешних нагрузок, длины трещины, формы тела и определяемый решением упругой задачи в целом.

Разрушение теснейшим образом связано с процессами, которые про­текают в окрестности кончика трещины. Поэтому большое значение для анализа процесса разрушения имеют формулы определения напряжений, и перемещений вблизи кончика трещины (рис. 4).

 

 

Рис.4

 

В случае нормального отрыва:

(4)

где μ - модуль сдвига; X = 3-4ν для плоской деформации; X =(3-ν)/(1+ν) для обобщенного плоского напряженного состоя­ния; ν - коэффициент Пуассона; u и V - проекции вектора перемещения соответственно на оси X , у •

В случае поперечного сдвига:

 

(5)

 

где КII - коэффициент интенсивности напряжений поперечного сдвига

В случае продольного сдвига:

(6)

 

где τху , τxz, τyz - касательные напряжения; W - проекция вектора перемещения на ось z ; KIII- коэффициент интенсивности на­пряжения продольного сдвига.

В условиях плоской деформации W = 0 Ϭz=Ʋ(Ϭx+Ϭy),тог­да как в условиях обобщенного плоского напряженного состояния Ϭz= О .

Из формул (4)…(6), где отброшены члены более высокого порядка относительно переменной р , следует, что напряжения при р → О стремятся к бесконечности. Это является следствием математическо­го приближения-линеаризации, связанной с удовлетворением гранич­ных условий на недеформированной поверхности трещины (щели) и ис­пользование закона Гука. Закон Гука становится неверным при больших внутренних напряжениях в материале, возникяших при сильной концентрации напряжений в окрестности краев трещины. Поэтому формулы (4)…(6) перестают отвечать действительности при очень ма­лых r<r0 . Однако при достаточно малых r>r0 формулы (4)..

(6) могу служить для асимптотической оценки свойств поля напряженй в окрестности вершины трешины.

Условие разрушения Ирвина

Все процессы разрушения материала определяются интенсивностью поля напряжений в области, окружающей кончик трещины, и характеразуются коэффициентом интенсивности напряжений . Дж. Ирвин предложил следующее условие разрушения: трещина начинает расти, когда коэффициент интенсивности напряжений достигает некоторого критического значения.

Значение КI , при достижении которого трещина будет распространяться неустойчиво, является константой материала, называемой вязкостью разрушения или критическим коэффициентом интенсивности напряжений. Критический коэффициент интенсивности напряжений при статическом приложении нагрузки в условиях плоской деформации обозначается КI C . а при плоском напряженном состоянии Кс • Таким образом, условие разрушения для тела с трещиной имеет вид

Следовательно, трещина, имеющаяся в детали или элементе конструкции, расти не будет, если KI <К1с или КI <Кс .

Коэффициент интенсивности KI зависит от нагрузки, размера трещины и геометрии детали и определяется, как правило, теоретиче­ски с использованием методов теории упругости. Коэффициенты К1С и Кс определяются экспериментально, являются постоянными материала и зависят от температуры и скорости деформации. Значение Кс зависит, кроме того, от толщины пластины.