Похідні вищих порядків. Нехай функція y = f (x) має похідну у будь-якій точці x інтервалу ]a, b[
Нехай функція y = f (x) має похідну у будь-якій точці x інтервалу ]a, b[. Тоді ця похідна y¢ = f ¢(x) сама є функцією, визначеною в інтервалі ]a, b[, і можна шукати її похідну в точках цього інтервалу. Назвемо f ¢(x) першою похідною, або похідною першого порядку функції f (x).
Означення. Другою похідною функції f (x) у точці x (похідною другого порядку) називається похідна (якщо вона існує) від її першої похідної y цій точці.
Позначається друга похідна функції y = f (x) по-різному: f ¢¢(x),  ,
,  ,
,  ,
,  , або просто y¢¢, якщо зрозуміло, яка змінна є аргументом. Отже, за означенням,
, або просто y¢¢, якщо зрозуміло, яка змінна є аргументом. Отже, за означенням,
 .
.
Якщо функція y = f (x) має у точці x другу похідну, то вона називається двічі диференційовною у цій точці. Функція двічі диференційовна у інтервалі ]a, b[, якщо вона двічі диференційовна у кожній точці цього інтервалу.
Механічний зміст другої похідної. Нехай s = s(t) – рівняння прямолінійного руху і відома швидкість v(t) = s¢(t) у момент t, яка змінюється з часом. За час Dt вона зміниться на величину Dv. Середнє прискорення ac дорівнює відношенню приросту швидкості Dv за час Dt до цього часу: b  .
.
За прискорення в момент t приймають границю середнього прискорення, коли Dt ® 0. Отже,  ,
,
або, враховуючи, що v(t) = s¢(t), маємо  .
.
Т. ч., прискорення прямолінійного руху – це друга похідна від шляху по часу.
Приклад. Знайти другу похідну функції  .
.
Розв’язання. 
Тому
 .
.
Аналогічно можна визначити третю похідну f ¢¢¢(x) (похідну третього порядку) функції y = f (x) у точці x як похідну від її другої похідної. А саме,
 .
.
Похідні вищих порядків позначаються ще й за допомогою римських чисел: yIV, yV тощо.
Означення.n-ю похідною (похідною n-го порядку) функції
y = f (x) у точці x називається похідна від її (n – 1)-ї похідної:
f (n)(x) = y(n)(x) = (y(n – 1)(x))¢ =  .
.
Нехай функція y = y(x) задана неявно рівнянням
F(x, y) = 0, де y = y(x).
Ми уже знаємо як знайти першу похідну 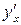 . Другу похідну
. Другу похідну  знаходимо як похідну від
знаходимо як похідну від 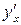 , а потім, якщо у виразі для
, а потім, якщо у виразі для  з’явиться
з’явиться 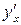 , то підставимо її значення.
, то підставимо її значення.
Приклад. Функція y = y(x)задана неявно рівнянням b2x2 +a2y2 = a2b2. Знайти  .
.
Розв’язання. Знаходимо 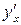 :
:  ;
;
 ;
;  .
.
Знаходимо  :
:  .
.
В цей вираз підставляємо 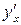 :
:  .
.
Використовуючи те, що b2x2 + a2y2 = a2b2, матимемо остаточно
 .
.
Аналогічно знаходимо похідні третього і більш високого порядку.
Нехай функція y = y(x)задана параметрично рівняннями x = x(t), y = y(t).
Ми встановили формулу для її першої похідної:  ,
,
яка, взагалі кажучи, є функцією змінної t. Отже, похідну від 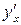 потрібно знову шукати як похідну функції, заданої параметрично, тобто
потрібно знову шукати як похідну функції, заданої параметрично, тобто  .
.
Приклад. Нехай функція задана параметрично: x = Rcos3 t, y = Rsin3 t. Знайти  .
.
Розв’язання. Знаходимо 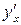 :
:  .
.
Знаходимо  за формулою
за формулою  .
.