Тема 1 РІВНЯННЯ МАТЕМАТИЧНОЇ ФІЗИКИ
В.А. Петрук, М.Б. Ковальчук, Н.В. Сачанюк-Кавецька
ВИЩА МАТЕМАТИКА З КОМП’ЮТЕРНОЮ ПІДТРИМКОЮ.
РІВНЯННЯ МАТЕМАТИЧНОЇ ФІЗИКИ
 |
УДК 517.958 (075):004.855.5
П 31
Рецензенти:
Н.Т.Тверезовська, доктор педагогічних наук, професор
С.В. Павлов, доктор технічних наук, професор
О.М. Джеджула, доктор педагогічних наук, професор
Петрук В.А., Ковальчук М.Б., Сачанюк-Кавецька Н.В.
П 31 Вища математика з комп’ютерною підтримкою. Рівняння математичної фізики. Навчальний посібник. – Вінниця: ВНТУ, 2010. –157 с.
В посібнику розглянуто достатню кількість рівнянь математичної фізики; теоретичні положення про класифікацію диференціальних рівнянь з переліком класу задач, в яких вони використовуються і програмним варіантом їх розв’язування в системі Maple; методи розв’язування рівнянь. Істотною особливістю даного посібника є розгляд спеціальних функцій математичної фізики, їх використання при розв’язуванні диференціальних рівнянь у частинних похідних, а також розгляд динамічних моделей коливання скінченної і нескінченної струни, прямокутної та круглої мембрани. Динаміка розгляду цих моделей забезпечується засобами Maple.
До кожної теми розроблені питання для самоперевірки та розглянуто по 30 варіантів завдань для самостійної роботи, що дозволяє використовувати посібник для практичних занять.
Посібник розрахований на студентів технічних спеціальностей.
УДК 517. 958 (075):004.855.5
©В.А. Петрук,
М.Б. Ковальчук,
Н. В. Сачанюк-Кавецька,
З М І С Т
ПЕРЕДМОВА. 4
Тема 1 РІВНЯННЯ МАТЕМАТИЧНОЇ ФІЗИКИ. 6
1.1 Рівняння малих поперечних коливань струни. 6
1.2 Рівняння малих поздовжніх коливань стержня. 8
1.3 Рівняння малих поперечних коливань мембрани. 9
1.4 Телеграфне рівняння. 13
1.5 Рівняння теплопровідності 16
1.6 Рівняння поширення тепла в стержні 18
1.7 Основні рівняння математичної фізики. 21
Питання для самоперевірки. 23
Завдання для самостійної роботи. 24
Тема 2 ЗВЕДЕННЯ РІВНЯНЬ ДРУГОГО ПОРЯДКУ ДО КАНОНІЧНОГО ВИГЛЯДУ ЗА
ДОПОМОГОЮ ЗАМІНИ ЗМІННИХ. 28
2.1 Рівняння гіперболічного типу. 30
2.2 Рівняння еліптичного типу. 33
2.3 Рівняння параболічного типу. 35
2.4 Розв’язування задачі Коші для рівняння коливання струни методом
характеристик (формула Д’Аламбера) 45
Питання для самоперевірки. 53
Завдання для самостійної роботи. 54
ТЕМА 3 МЕТОД ФУР’Є. 57
3.1 Розв’язання методом Фур’є першої крайової задачі для рівняння малих
поперечних коливань струни. 57
3.2 Розв’язання методом Фур’є першої крайової задачі для рівняння
теплопровідності 60
3.3 Розв’язання методом Фур’є першої крайової задачі 66
3.4 Приклади розв’язання задачі Коші для рівняння теплопровідності 74
Питання для самоперевірки. 105
Завдання для самостійної роботи. 106
ТЕМА 4 МЕТОД СІТОК ДЛЯ РІВНЯННЯ ПАРАБОЛІЧНОГО ТИПУ. 111
Питання для самоперевірки. 119
Завдання для самостійної роботи. 120
ТЕМА 5 СПЕЦІАЛЬНІ ФУНКЦІЇ МАТЕМАТИЧНОЇ ФІЗИКИ. 123
5.1 Інтеграл Ейлера першого роду. 123
5.2 Інтеграл Ейлера другого роду. 124
5.3 Функція Бесселя. 124
5.4 Рекурентні формули для функції Бесселя. 127
5.5 Інтегральне представлення Пуассона функції Бесселя та його
використання. 128
5.6 Сферичні функції. Поліноми Лежандра. 131
5.7 Виробнича функція для поліномів Лежандра. 134
5.8 Рекурентні формули для поліномів Лежандра. 135
Питання для самоперевірки. 141
Завдання для самостійної роботи. 142
ВІДПОВІДІ 146
ЛІТЕРАТУРА. 155
ПРЕДМЕТНИЙ ПОКАЖЧИК. 156
ПЕРЕДМОВА
Математична фізика – це математичний апарат вивчення фізичних полів. Цей апарат є основою теоретичної гідромеханіки, теорії теплопровідності, теорії пружності, класичної теорії електромагнітного поля.
Математична фізика не обмежується тільки отриманням математичних співвідношень, що описують отримані експериментальним шляхом залежності між фізичними величинами. Розв’язування задач математичної фізики сприяє виникненню нових ідей та теорій. Класичним прикладом тут є історія відкриття античастинок. Як відомо, першим було відкрито позитрон. Його існування було передбачено Полем Діраком у 1926 році як математичний наслідок квантової теорії руху електронів. І тільки у 1932 році позитрони були фактично спостережені.
Побудова та дослідження математичних моделей фізичних явищ складають предмет математичної фізики. Математична фізика розвивалася з часів Н’ютона паралельно розвитку фізики та математики. У XVIII ст. методи математичної фізики почали формуватись при вивченні коливань струни та стержня, а також при розв’язуванні задач, пов’язаних з акустикою та гідродинамікою. У цей же час закладаються підвалини теоретичної механіки (Ж. Даламбер, Л. Ейлер, П. Лаплас, Д. Бернуллі). У XIX ст. ідеї математичної фізики піднялися на інший виток розвитку у зв’язку із задачами теплопровідності, дифузії, пружності, оптики, електродинаміки. У цей же період створюються теорії потенціалу та теорія стійкості руху (Ж. Фур’є, К. Гаусс, О. Коші, М.В. Остроградський,
П. Діріхле, Д. Стокс). У ХХ ст. до математичної фізики залучаються задачі квантової фізики та теорії відносності, а також нові проблеми газової динаміки, переносу частинок та фізики плазми.
Основними математичними засобами дослідження усіх цих задач є теорія диференціальних рівнянь, теорія функцій, функціональний аналіз, теорія ймовірностей, наближені методи та обчислювальна математика.
Для кращого розуміння подальшого викладення матеріалу наведемо основні означення.
Означення 1. Диференціальним рівнянням у частинних похідних називається рівняння, яке пов’язує незалежні змінні, їх функцію і частинні похідні від цієї функції.
Наприклад,
; (*)
(**)
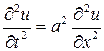Означення 2. Найвищий порядок частинної похідної, що входить у рівняння, називається порядком диференціального рівняння у частинних похідних.
Наприклад, рівняння (*) є рівнянням другого порядку, а рівняння (**) – першого.
Означення 3. Диференціальне рівняння у частинних похідних називається лінійним, якщо воно лінійне відносно невідомої функції і її частинних похідних.
Означення 4. Диференціальне рівняння у частинних похідних називається квазілінійним, якщо воно лінійне відносно похідних найвищого порядку.
Означення 5. Розв’язком диференціального рівняння у частинних похідних називається усяка функція, неперервна в області, у якій ставиться задача, що всередині області має неперервні частинні похідні, порядок яких відповідає порядку диференціального рівняння і при підстановці у це рівняння перетворює його на тотожність за незалежними змінними.
Для того, щоб повністю описати той чи інший процес, необхідно, окрім самого рівняння у частинних похідних, задати початковий стан цього процесу (початкові умови) та режим роботи на границі області, у якій відбувається процес (граничні умови). Математично це пов’язано із нескінченною кількістю розв’язків диференціальних рівнянь. Тому, щоб виділити розв’язок, який описує реальний процес, необхідно задати додаткові умови. Такими додатковими умовами і є крайові умови – початкові та граничні. Відповідна задача називається крайовою задачею або задачею математичної фізики.
Означення 6. Сукупність диференціального рівняння у частинних похідних і додаткових умов (крайових та початкових) становить математичне моделювання фізичної задачі і називається задачею математичної фізики.
Та обставина, що задача математичної фізики повинна моделювати деяке фізичне явище (процес), накладає на неї ряд вимог, часто не обов’язкових для суто математичних задач. Так, задача математичної фізики вважається поставленою коректно (правильно), якщо існує її розв’язок єдиний і стійкий. При цьому, стійкість розв’язку означає, що малим змінам в умові задачі повинні відповідати малі зміни у розв’язку, що дозволить знівелювати похибку експериментальних даних задачі. Природно, що основною проблемою «Теорії рівнянь математичної фізики» є знаходження розв’язку задачі математичної фізики у вигляді, зручному для практики. Знаючи цей розв’язок, можна отримати кількісну характеристику процесу у будь-якій точці середовища і у будь-який момент часу.
Тема 1 РІВНЯННЯ МАТЕМАТИЧНОЇ ФІЗИКИ
Широкий клас фізичних процесів описується лінійними диференціальними рівняннями другого порядку
. (1.1)
Розглянемо характерні фізичні процеси, що зводяться до різних крайових задач для диференціальних рівнянь типу (1.1), класифікацію таких рівнянь.
1.1 Рівняння малих поперечних коливань струни
Розглянемо натягнену струну, закріплену на кінцях 
та 
. Моделюючи струну будемо нехтувати її товщиною, вважаючи струну ниткою, а також силами, що виникають при згинанні, та силами ваги. Залишаємо тільки сили натягу, які описуються законом Гука: натяг струни пропорційний видовженню. Таким чином, моделлю струни є пружна, невагома й абсолютно гнучка нитка.
За основну величину, що характеризує процес коливання струни, виберемо вектор зміщення точок струни від положення рівноваги. Натяг, що виникає у струні у будь-який момент часу, направлений по дотичній до профілю.
Розглянемо малі відхилення точок струни від положення рівноваги, при яких можна вважати, що рух усіх точок струни відбувається в одній площині і перпендикулярно до осі 
. При цьому довжина елементарної дуги струни дорівнює її проекції на цю вісь. Отже, за зроблених припущень, видовження струни під час її малих коливань не відбувається. Тоді за законом Гука величина натягу 
в кожній точці струни не змінюється з часом.
Знайдемо проекції на вісь 
сил натягу, що діють на елементарну дугу струни 
: 
(рис. 1.1).
Рисунок 1.1
Оскільки кут 
досить малий, то можна вважати, що 
еквівалентний 
.
Тоді
,
але за теоремою Лагранжа одержуємо
, де 
.
Для отримання рівняння руху точок струни потрібно зовнішні сили прирівняти до сил інерції. На підставі закону Д’Аламбера всі сили, які діють на ділянку 
, повинні врівноважуватись.
Нехай 
- лінійна густина струни, тоді маса елемента струни дорівнює 
. Прискорення елемента струни дорівнює 
. Тоді за законом Д’Аламбера маємо:
. (1.2)
З формули (1.2), враховуючи, що 
, одержуємо рівняння малих поперечних коливань струни
(1.3)
з крайовими умовами
(1.4)
та початковими умовами
, (1.5)
де 
- форма струни у початковий момент;
, (1.6)
де 
- швидкість у кожній точці струни у початковий момент.
1.2 Рівняння малих поздовжніх коливань стержня
Розглянемо стержень, розташований вздовж осі .
Введемо такі позначення:
S(x) – площа перерізу стержня площиною, перпендикулярною до осі і проведеною через точку Х;
К(х) – модуль Юнга;
ρ(х) – густина у перерізі стержня з абсцисою х;
U(x,t) – величина відштовхування (вздовж стержня) перерізу стержня з абсцисою х в момент часу t.
Припустимо, що величина відштовхування усіх точок фіксованого розрізу однакова. Зрозуміло, що в межах даної моделі повздовжні коливання повністю описуються формулою U(x,t).
Малими коливаннями називаються такі повздовжні коливання, в яких натяги, що виникають в процесі коливання, відповідають закону Гука.
Підрахуємо відносне видовження площі пластини (х; х+Δх) в момент часу t. Координати кінців цієї частини площі: х+ U(x,t), х+ Δх+ U(х+Δх, t).
Відносне видовження частини площі:
де 0<θ<1.
Таким чином, відносне видовження в точці Х в момент часу t дорівнює 
, а величина натягу Т за законом Гука:
.
Візьмемо f(x,t) – густина рівнодійних зовнішніх сил, які діють на переріз з абсцисою Х вздовж осі х.
Згідно з другим законом Н’ютона на відрізку 
за час 
маємо: 
– рівняння малих повздовжніх коливань ділянки стержня 
у інтегральній формі.
Припустимо існування неперервних похідних другого порядку функції U(x,t) і неперервної першої похідної функцій K(x) та S(x), знайдемо диференціальні рівняння малих повздовжніх коливань стержня:
. (1.7)
Якщо S(x), K(x) та ρ(x) – сталі, то припущення існування 
та 
правильне і рівняння (1.7) зведемо до вигляду:
(1.8)
1.3 Рівняння малих поперечних коливань мембрани
Мембраною називається тонка натягнута плоска плівка, що не чинить опір згину і зсуву, але чинить опір розтягуванню.
(1.9)
Якщо густина 
постійна, то рівняння коливань мембрани
називається двовимірним хвильовим рівнянням.
Наведемо виведення рівняння (1.9). Розглядатимемо малі поперечні коливання мембрани, в яких відбувається зсув перпендикулярно до площини мембрани, за яку ми приймемо площину 
. Нехай 
- величина зсуву точки з координатами ( 
) у момент часу 
. Критерієм малості коливань слугують умови
.
Нехай 
— елемент дуги деякого контура, що лежить на поверхні мембрани, М — точка цього елемента. На цей елемент діють сили натягу 
. Відсутність опору мембрани згину і зсуву математично виражається у тому, що вектор натягу лежить в площині, дотичній до поверхні мембрани в точці М, і перпендикулярний до елемента , а натяг в цій точці не залежить від напряму елемента , що містить точку М. З припущення про малість коливань випливає:
– проекція Tпр вектора натягу 
на площину ( ) рівна ;
– натяг не залежить від часу .
Дійсно, Tпр = 
, де 
- кут між вектором і площиною ( ).
Але не більше кута 
між дотичною площиною до поверхні мембрани, в якій лежить вектор , і площиною ( ): 
. 
. Тому
 |
Отже,
, і значить, Tпр 
.
Далі розглянемо ділянку S незбуреної мембрани. Її площа дорівнює
.
Площа цієї ділянки у момент часу дорівнює
.
Таким чином, площа фіксованої ділянки мембрани не змінюється з часом, тобто ділянка не розтягується. Тому за законом Гука і не змінюється з часом. З того, що вектор направлений по перпендикуляру до елемента дуги , випливає, що не залежить також від 
і 
.
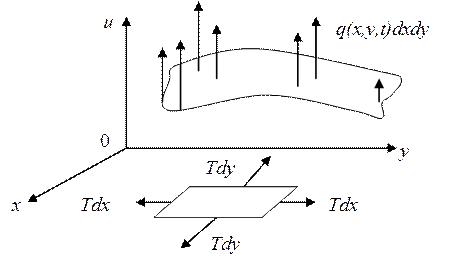
Розглянемо елемент мембрани, для якого точка N(x,y,u) — середня. На цей елемент, окрім сил натягу , діє зовнішнє розподілене по поверхні навантаження q(x,y,t), розраховане на одиницю площі і перпендикулярне до поверхні мембрани (рис. 1.2). Рівнодіюча зовнішніх сил буде рівна q(x,y,t) dxdy. Рівнодійна сил натягу
 |
Позначимо через
поверхневу густину мембрани (густину, розраховану на одиницю площі). Тоді маса даного елемента мембрани буде dxdy. Таким чином, згідно з законами Ньютона ми можемо написати рівняння
(1.10)
Величина 
має розмірність швидкості. Вона характеризує швидкість поширення коливань. В окремому випадку може бути
q(x, у, t)= 0, тоді ми маємо рівняння вільних коливань мембрани
. (1.11)
Для завершення постановки задачі про коливання мембрани задамо початкові і крайові умови.
Початкові умови:
. (1.12)
Крайові умови на контурі Г:
. (1.13)
Задача про рівновагу мембрани
Якщо вважати, що q=q(x,y), тобто, зовнішнє поперечне навантаження не залежить від часу, то можна ставити задачу про рівновагу мембрани. Рівняння рівноваги можна вивести безпосередньо або його можна одержати з рівняння коливань. Рівняння рівноваги мембрани має вигляд
. (1.14)
Це рівняння належить інтегрувати з крайовою умовою, наприклад, з умовою вигляду (1.13). Початкові умови не ставляться.
Задача про сталі синусоїдні коливання мембрани
Нехай q=q(x,y,t) залежить від часу спеціальним чином
,
або
,
де 
– частота зовнішньої збурюючої сили.
В цьому випадку і розв’язання задачі доцільно шукати у вигляді
,
або
,
відповідно.
Після підстановки цих функцій u(x,y,t) в рівняння коливань мембрани одержимо рівняння
, (1.15)
яке належить інтегрувати за крайових умов, наприклад, у вигляді (1.13).
1.4 Телеграфне рівняння
Як ще один приклад хвильового рівняння розглянемо телеграфне рівняння, яке застосовується в теорії поширення квазістаціонарних електричних коливань по кабелях.
Якщо протяжність електричного ланцюга велика (наприклад, телеграфні лінії або лінії передачі енергії), то такий ланцюг не можна характеризувати зосередженими параметрами (опором, ємністю, котушкою самоіндукції). У найпростішому випадку, коли електричний ланцюг має велику протяжність, можна говорити про лінії з розподіленими параметрами. При вивченні таких ліній враховують опір проводів, індуктивність лінії, витік струму в атмосферу внаслідок відсутності ізоляції проводами дротами (або між проводом і землею). Ми розглядатимемо однорідну лінію, тобто лінію, для якої опір, індуктивність, витік і ємність розподілені уздовж проводу безперервно і рівномірно; для наочності вважатимемо лінію двопровідною (рис. 1.3).
 |
Припустимо, що лінія електропередачі характеризується омічним опором R, самоіндукцією L, ємністю С і витоком ізоляції g, розрахованими на одиницю довжини. Нехай напруга між проводами і струм на відстані х від початку лінії х = 0 у момент часу t рівні, відповідно, u(х,t) і I(x,t). Ці функції і є шуканими; вони пов'язані двома диференціальними рівняннями, які ми зараз виведемо.
Нагадаємо, що самоіндукція L — коефіцієнт пропорційності, що зв'язує електрорушійну силу самоіндукції із швидкістю зміни струму, тобто, 
. Ємність С — коефіцієнт пропорційності між струмом зсуву і швидкістю зміни напруги, тобто 
. Останню рівність отримуємо диференціюванням співвідношення 
, де q — кількість електрики, яка залишається на ділянці проводу, що розглядається як обкладка конденсатора, а u – напруга. Нарешті, витік g є коефіцієнтом пропорційності між струмом витоку і напругою.
Для складання диференціальних рівнянь, якім повинні задовольняти функції u(х,t) і I(x,t), виділимо ділянку проводу від точки з абсцисою х до точки з абсцисою х + dx. Якщо напруга і струм в точці х у момент часу t рівні, відповідно, u(х,t) і I(x,t), то в точці х + dx в той же момент часу значення цих величин (з точністю до нескінченно малих вищих порядків у порівнянні з dx) будуть рівні 
і 
. Падіння напруги на даній ділянці викликатиметься втратою напруги в проводі, тобто величиною RdxI, і виникненням протидіючої електрорушійної сили самоіндукції. Тому
,
тобто,
. (1.16)
Далі зміна струму на цій же ділянці обумовлена струмом витоку і струмом зсуву. Отже,
,
звідки
. (1.17)
Велике значення мають початкові і крайові умови, які повинні виконуватися на кінцях лінії. Початкові умови в загальному випадку формулюються так:
.
Користуючись рівняннями (1.16) і (1.17), легко знайти 
і 
при
t = 0.
Якщо на початку лінії х=0 включено джерело живлення з електрорушійною силою Е, а на кінці 
є приймач струму з опором Rl, то крайові умови будуть
.
Зокрема, якщо один кінець х=0 підтримується під напругою Е, а інший коротко замкнутий, ми маємо
.
Якщо, наприклад, кінець 
лінії відкритий, то в цьому кінці ми повинні мати
.
Взагалі, якщо в кінці ( ) лінії включені зовнішня електрорушійна сила Е, опір R і самоіндукція I, то в ньому ми повинні мати
.
Зрозуміло, можна розглядати будь-яку комбінацію умов при і 
. Виключимо струм з рівнянь (1.16) і (1.17), одержимо
(1.18)
Рівняння (1.18) називається телеграфним рівнянням; — швидкість передачі сигналу по кабелю.
Через симетрію рівнянь (1.16) і (1.17) аналогічне рівняння виходить і для струму І (заміною в (1.17) напруги u на струм I).
Якщо вважати 
, 
, то замість рівняння (1.18) ми матимемо рівняння для лінії без втрат
.
1.5 Рівняння теплопровідності
Процес поширення тепла або дифузії частинок у середовищі описується таким загальним рівнянням:
. (1.19)
Отримаємо його для випадку поширення тепла.
Позначимо 
температуру середовища в точці 
у момент часу t. Середовище будемо вважати ізотропним. Виділимо всередині тіла деякий об’єм V, обмежений гладкою або кусково-гладкою поверхнею S, в об’єм V надходить кількість тепла (потік тепла)
, (1.20)
де n – зовнішня нормаль до поверхні S у точці М;
k - коефіцієнт теплопровідності.
Оскільки
– похідна за напрямком, яку можна розглядати як скалярний добуток двох векторів
та
,
то
.
Позначивши
,
матимемо:
. (1.21)
Застосуємо до правої частини рівності (1.21) формулу Остроградського-Гаусса, за якою
. (1.22)
Якщо є теплові джерела, то в об’ємі V виникає тепло, яке дорівнює
, (1.23)
де 
– питома потужність джерела.
Щоб вивести рівняння теплопровідності, складемо рівняння теплового балансу. Виділення тепла з об’єму V повинно супроводжуватися зменшенням температури точок тіла. Якщо температура у точці М в момент часу t була 
, то в момент 
вона дорівнюватиме 
. З курсу фізики відомо, яка кількість тепла виділяється тілом масою m, якщо його температура змінюється на 
і дорівнює
,
де 
– теплоємність.
Тоді в усьому об’ємі ця кількість тепла дорівнюватиме
. (1.24)
Запишемо рівняння теплового балансу:
. (1.25)
Підставимо знайдені значення 
, 
, 
з (1.21), (1.23) і (1.24) у рівняння (1.25), матимемо:
. (1.26)
Поділимо обидві частини рівності (1.26) на 
і перейдемо до границі за умови, що 
, дістанемо:
,
або
. (1.27)
Для неперервних функцій і їх частинних похідних матимемо, що
. (1.28)
Рівняння (1.28) називається рівнянням теплопровідності.
Якщо середовище однорідне, то 
, 
, 
. Тоді рівняння теплопровідності матиме вигляд:
, (1.29)
де 
,
– оператор Лапласа, 
,
,
.
1.6 Рівняння поширення тепла в стержні
Розглянемо однорідний стержень довжиною l. Будемо вважати, що бічна поверхня стержня теплонепроникна і що в усіх точках поперечного перерізу стержня температура однакова. Вивчимо процес поширення тепла в стержні.
Розмістимо вісь Ох так, щоб один кінець стержня збігався з точкою х=0, а другий – з точкою х=R.
Нехай 
- температура в перерізі стержня з абсцисою х у момент часу t. Кількість тепла, яка проходить через поперечний переріз стержня з абсцисою х за одиницю часу визначається за формулою:
, (1.30)
де 
– площа перерізу стержня;
k – коефіцієнт теплопровідності.
Розглянемо елемент стержня, що міститься між перерізами з абсцисами х1 та х2 (х1–х2=∆х). Кількість тепла, що проходить через переріз стержня з абсцисою х, за час 
дорівнює:
, (1.31)
а для перерізу з абсцисою х2:
. (1.32)
Приріст кількості тепла 
в елементі стержня за час дорівнюватиме:
.
При малих 
( 
) вираз у дужках замінимо диференціалом:
.
Тоді
. (1.33)
Цей приріст тепла за час також витрачається на підвищення температури елемента стержня на величину 
(1.34)
або
(1.35)
де с – теплоємність речовини стержня;
– густина речовини стержня;
– маса елемента стержня.
Прирівнюючи вирази (1.34) і (1.35) для однієї і тієї ж кількості тепла 
, дістанемо:
,
або
.
Позначимо через
,
матимемо рівняння:
. (1.36)
Це і є рівняння поширення тепла в однорідному стержні.
Задамо ще крайові умови:
(1.37)
та початкову умову (для 
):
(1.38)
Початкова умова (1.38) відповідає тому, що для 
у різних перерізах стержня задана температура, яка дорівнює 
. Крайові умови (1.37) відповідають тому, що на кінцях стержня для х=0 і х=l підтримується температура рівня 
і 
, відповідно.
1.7 Основні рівняння математичної фізики
У попередніх параграфах ми ознайомилися з різноманітними задачами фізики та механіки, що приводять до рівнянь з частинними похідними. Але основною метою є не виведення рівняння у частинних похідних, а їх дослідження та розв’язування. Тому потрібно перерахувати основні найбільш уживані рівняння математичної фізики (на прикладі лінійних рівнянь в частинних похідних другого порядку).
1. Рівняння Лапласа (рівняння еліптичного типу)
. (1.39)
Використовується рівняння Лапласа при вивченні стаціонарних процесів поширення тепла, процесу стаціонарного явища дифузії і фільтрації, при дослідженні потенціалів полів тяжіння, стаціонарних електричних полів в яких відсутні відповідні маси та електричні заряди.
2. Хвильове рівняння (рівняння гіперболічного типу) 
, (1.40)
де а – числовий коефіцієнт, який визначається в залежності від виду задачі.
Хвильове рівняння використовують там, де виникає потреба дослідити хвильові процеси: поперечні коливання струни, поздовжні коливання стержня, електричні коливання у проводах, газові коливання тощо.
У тривимірному координатному просторі розглядається тривимірне хвильове рівняння
. (1.41)
Це рівняння описує процеси поширення звуку в однорідному середовищі і електромагнітних хвиль в однорідному непровідному середовищі. Його задовольняють густина і тиск газу, потенціал швидкостей, а також складові напруженості електричного і магнітного полів і відповідні потенціали.
3. Рівняння теплопровідності (рівняння параболічного типу)
. (1.42)
Рівняння використовуються при дослідження розподілу тепла, дослідженні явища дифузії, фільтрації тощо.
4. Рівняння Пуассона
. (1.43)
Рівняння Пуассона, на відміну від рівняння Лапласа, описує поля із розподіленими внутрішніми джерелами. Ці рівняння зустрічаються майже у всіх областях прикладної фізики.
5. Рівняння Гельмгольця
. (1.44)
Це рівняння для амплітуд сталих періодичних коливань заданої частоти; 
– хвильове число.
7. Поширення хвиль у середовищах із поглинанням енергії описується рівнянням
. (1.45)
Питання для самоперевірки
1. Що називається диференціальним рівнянням у частинних похідних?
2. Що називається розв’язком диференціального рівняння у частинних похідних?
3. Як визначається порядок диференціального рівняння у частинних похідних?
4. Що називається задачею математичної фізики?
5. Запишіть загальний вигляд лінійного диференціального рівняння у частинних похідних другого порядку.
6. Запишіть загальний вигляд хвильового рівняння.
7. Що називається струною? Виведіть рівняння малих поперечних коливань струни.
8. Що називається стержнем? Виведіть рівняння поздовжніх коливань стержня.
9. Що називається мембраною? Виведіть рівняння поперечних коливань мембрани.
10. Сформулюйте задачу про рівновагу мембрани.
11. Сформулюйте задачу про сталі синусоїдні коливання мембрани.
12. Виведіть телеграфне рівняння.
13. Напишіть тривимірне хвильове рівняння.
14. Виведіть рівняння теплопровідності.
15. Сформулюйте крайові умови для рівняння теплопровідності.
16. Сформулюйте крайові умови для одновимірного хвильового рівняння на прикладах поперечних коливань струни та поздовжніх коливань стержня.
17. Напишіть рівняння Лапласа та рівняння Пуассона. До якого типу відносяться ці рівняння?
18. Напишіть рівняння Гельмгольця. Які процеси описує це рівняння?
19. Які фізичні процеси описуються за допомогою рівнянь параболічного типу?
20. Які фізичні процеси описуються за допомогою рівнянь гіперболічного типу?
21. Які фізичні процеси описуються за допомогою рівнянь еліптичного типу?
22. Виведіть рівняння поширення тепла в стержні. Сформулюйте крайові та початкові умови.
Завдання для самостійної роботи
1. Знайти статистичний прогин струни, закріпленої на кінцях, під дією неперервно розподіленого навантаження (на одиницю довжини).
2. Вивести рівняння малих поперечних коливань струни із насадженою на неї у деякій точці 
бусинкою маси 
.
3. Вивести рівняння коливань струни, що відбуваються у пружному середовищі.
4. Крутильними коливаннями стержня називають такі коливання, при яких його поперечні перерізи повертаються один відносно одного, обертаючись при цьому навколо стержня. Вивести рівняння малих крутильних коливань однорідного циліндричного стержня, якщо кінці стержня вільні.
5. Крутильними коливаннями стержня називають такі коливання, при яких його поперечні перерізи повертаються один відносно одного, обертаючись при цьому навколо стержня. Вивести рівняння малих крутильних коливань однорідного циліндричного стержня, якщо кінці стержня жорстко закріплені.
6. Точкам пружного однорідного прямокутного стержня, жорстко закріпленого на лівому кінці і вільного на правому, у початковий момент часу 
надано малі поперечні відхилення і швидкості, паралельні поздовжній площині симетрії стержня. Сформулювати крайову задачу для визначення поперечних відхилень точок стержня при 
, припускаючи, що стержень здійснює малі поперечні коливання.
7. Знаходячись у горизонтальній площині невагома струна з постійною кутовою швидкістю 
обертається навколо вертикальної осі. Один кінець струни закріплений на осі, а інший вільний. У початковий момент часу точкам цієї струни надаються малі відхилення і швидкості по нормалях до цієї площини. Сформулювати крайові та початкові умови для визначення відхилень точок струни від площини рівноважного руху.
8. Нехай у точці 
нескінченної однорідної струни знаходиться кулька маси 
. Початкові швидкості і початкові відхилення точок струни рівню нулю. Сформулювати крайову задачу для визначення відхилень точок струни від положення рівноваги, якщо у початковий момент часу кулька отримує імпульс 
у поперечному напрямі.
9. У внутрішніх точках 
на струні зосереджені маси 
. Сформулювати крайову задачу для визначення малих поперечних коливань струни при довільних початкових даних. Кінці струни закріплені.
10. Кабель, що має потенціал 
, при заземлюється на одному кінці через зосереджену ємність (чи індуктивність), другий кінець ізольований. Скласти задачу про визначення електричного струму у кабелі.
11. Сформулювати крайову задачу для малих радіальних коливань ідеального однорідного газу, що знаходиться у трубці радіуса 
, яка простирається у обидві сторони на нескінченність. Початкові відхилення та початкові швидкості є заданими функціями від 
.
12. Сформулювати крайову задачу для малих радіальних коливань ідеального однорідного газу, що знаходиться у сферичній посудині радіуса , якщо початкові швидкості та початкові відхилення задано як функції від .
13. Сформулювати крайову задачу для поперечних коливань мембрани, до якої прикладено нормальний тиск 
на одиницю площі, якщо у незбуреному стані мембрана є плоскою, а навколишнє середовище не здійснює опору коливанням мембрани. Вважати, що мембрана жорстко закріплена на межі 
.
14. Сформулювати крайову задачу для поперечних коливань мембрани, до якої прикладено нормальний тиск на одиницю площі, якщо у незбуреному стані мембрана є плоскою, а навколишнє середовище не здійснює опору коливанням мембрани. Вважати, що мембрана вільна на межі .
15. Дано тонкий однорідний стержень довжиною 
, початкова температура якого 
. Сформулювати крайову задачу про визначення температури стержня, якщо на кінці підтримується стала температура 
, а на бічній поверхні та на кінці 
здійснюється конвективний теплообмін за законом Н’ютона з навколишнім середовищем нульової температури.
16. Сформулювати задачу про визначення температури у нескінченному тонкому теплоізольованому стержні, по якому з моменту у додатному напрямі із швидкістю 
починає рухатися точкове джерело, що дає 
одиниць тепла у одиницю часу.
17. Сформулювати задачу про охолодження тонкого однорідного кільця радіуса , на поверхні якого здійснюється конвективний теплообмін із навколишнім середовищем, яке має задану температуру. Нерівномірністю розподілу температури по товщині кільця знехтувати.
18. Необмежений циліндр радіуса має початкову температуру 
. Сформулювати крайову задачу про радіальне розповсюдження тепла, якщо бічна поверхня має постійну температуру.
19. Початкова температура необмеженої пластини товщиною 
дорівнює нулю. Сформулювати крайову задачу про розподіл температури при по товщині пластини, якщо вона нагрівається з обох боків рівними постійними тепловими потоками .
20. Початкова температура необмеженої пластини товщиною дорівнює нулю. Сформулювати крайову задачу про розподіл температури при , по товщині пластини, якщо в пластині, починаючи з моменту діє джерело тепла із постійною густиною 
, а її основи підтримуються при нульовій температурі.
21. Сформулювати крайову задачу про стаціонарний розподіл температури у тонкій прямокутній пластині ОАСВ із сторонами ОА=а, ОВ=b, якщо на бічних сторонах пластини підтримуються задані температури.
22. Сформулювати крайову задачу про стаціонарний розподіл температури у тонкій прямокутній пластині ОАСВ із сторонами ОА=а, ОВ=b, якщо на сторонах ОА і ОВ задано теплові потоки, а сторони ВС та АС теплоізольовані.
23. На плоску мембрану, обмежену кривою , діє стаціонарне поперечне навантаження із густиною 
. Сформулювати крайову задачу про відхилення точок мембрани від площини, якщо мембрана закріплена на краях.
24. На плоску мембрану, обмежену кривою , діє стаціонарне поперечне навантаження із густиною . Сформулювати крайову задачу про відхилення точок мембрани від площини, якщо край мембрани вільний.
25. На плоску мембрану, обмежену кривою , діє стаціонарне поперечне навантаження із густиною . Сформулювати крайову задачу про відхилення точок мембрани від площини, якщо край мембрани закріплений пружно.
26. Дано циліндр із радіусом основи та висотою 
. Сформулювати крайову задачу про стаціонарний розподіл температури всередині циліндра, якщо температура верхньої та нижньої основ є заданою функцією від , а бічна поверхня теплоізольована.
27. Дано циліндр із радіусом основи та висотою . Сформулювати крайову задачу про стаціонарний розподіл температури всередині циліндра, якщо температура верхньої та нижньої основ є заданою функцією від , а бічна поверхня має температуру, що залежить тільки від 
.
28. Дано циліндр із радіусом основи та висотою . Сформулювати крайову задачу про стаціонарний розподіл температури всередині циліндра, якщо температура верхньої та нижньої основ є заданою функцією від , а бічна поверхня вільно охолоджується у середовищі потрібної температури.
29. Дана однорідна куля радіуса із нульовою початковою температурою. Сформулювати крайову задачу про розподіл температури при всередині кулі, якщо куля нагрівається рівномірно по всій поверхні сталим тепловим потоком .
30. Дана однорідна куля радіуса із нульовою початковою температурою. Сформулювати крайову задачу про розподіл температури при всередині кулі, якщо на поверхні кулі відбувається конвективний теплообмін із навколишнім середовищем, температура якого залежить тільки від часу.