Відтворювані умови експерименту

Для кожного результату прямих вимірів знаходимо середнє значення і граничну похибку .

Середнє значення результату непрямих вимірювань

(29)

де – середні значення величин , виміряних безпосередньо.

Якщо гранична похибка середнього значення деякої величини 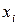дається з рівнем значущості , а для потрібен рівень значущості , то перераховуємо граничну похибку до заданої надійної ймовірності за формулою

(30)

де – коефіцієнт Стьюдента [MS Excel СТЬЮДРАСПОБР( )] для рівня значущості і нескінченної кількості вимірювань, – коефіцієнт Стьюдента для рівня значущості і нескінченної кількості вимірювань.

Гранична похибка результату непрямих вимірювань

(31)

де – частинні похідні від функції , взяті в точках середніх значень . Частинна похідна функції кількох змінних по одній з них, наприклад по x_i визначається формулою

(32)

У цьому випадку приріст отримує лише одна з незалежних змінних.

Похідні деяких найчастіше вживаних функцій наведені в табл. 2.3.

Таблиця 2.3

Похідні деяких функцій

Дуже часто функція має вигляд , де - показники степеня, які можуть бути як додатними, так і від’ємними. Можна показати, що в цьому випадку формула (31) набуває вигляду:

(33)

Результат непрямих вимірювань подаємо у вигляді:

(34)

із зазначенням одиниці вимірювання і надійної ймовірності.

Відносна гранична похибка середнього значення вимірюваної величини

(35)