Приклад виконання завдання
Дані, за якими виконуються розрахунки, наведені в табл. 6.1, кінцеві результати розрахунків заносяться до табл. 6.2
Таблиця 6.1
| Варіант | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| * | 0,1 | -100 | 0,90 |
Таблиця 6.2
| 
| 
| 
| 
| 
| 
|
| 88,8 | 5,31 | 5,06 | 0,2 | 0,109 | 5,2 | 5,9 |
Виконуємо обчислення і заносимо результати до табл. 6.3
Таблиця 6.3
|
|
|
|
|
|
| 
| |
| |||||||
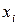
| 11,5 | 19,5 | 66,5 | 5,5 | 16,5 | 13,5 | - |
| 132,25 | 380,25 | 4422,25 | 30,25 | 272,25 | 182,25 | 5419,5 |
Знаходимо середнє значення вимірюваної величини
.
Знаходимо стандартну похибку окремого вимірювання
.
Знаходимо критерій промаху для максимального значення 
.
З табл. 1.2 для 
, 
знаходимо максимальне припустиме значення критерію промаху
.
Оскільки для критерій промаху 
, то значення 
є промахом і підлягає вилученню.
Виконуємо обчислення для решти значень і заносимо результати до табл. 6.4
Таблиця 6.4
|
|
|
|
|
|
| |
|
| ||||||
|
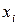
| 1,8 | 6,2 | 7,8 | 3,2 | 0,2 | - |
|
| 3,24 | 38,44 | 60,84 | 10,24 | 0,04 | 112,8 |
Знаходимо середнє значення вимірюваної величини
.
Знаходимо стандартну похибку окремого вимірювання
.
Знаходимо критерій промаху для максимального відхилення 
.
З табл. 1.2 для 
, знаходимо максимальне значення критерію промаху 
.
Оскільки для значення 
, що має максимальне відхилення , критерій промаху 
, то серія залишених результатів вимірювань не містить промахів.
З табл. 1.1 для , знаходимо коефіцієнт Стьюдента 
.
Знаходимо випадкову похибку середнього значення вимірюваної величини
.
Знаходимо паспортну похибку приладу
.
Знаходимо похибку приладу, перераховану на надійну ймовірність ,
.
Гранична похибка середнього значення вимірюваної величини
.
Результат вимірювань із надійною ймовірністю подаємо у вигляді:
.
Відносна гранична похибка середнього значення вимірюваної величини
.
Будуємо діаграму розподілу похибок окремих вимірів (рис. 6.1).
|
| Рис. 6.1. Розподіл похибок окремих вимірів. |
Таблиця 6.5
Похибки прямих вимірювань
| Варіант |
|
|
|
|
|
|
|
|
|
|
| 0,1 | 0,90 | |||||||||
| – | – | 0,2 | 0,95 | |||||||
| – | – | 0,5 | -25 | 0,90 | ||||||
| – | 1,0 | -50 | 0,95 | |||||||
| 0,1 | -25 | 0,90 | ||||||||
| 0,2 | 0,95 | |||||||||
| 0,5 | 0,90 | |||||||||
| – | 1,0 | 0,95 | ||||||||
| – | – | 0,1 | 0,90 | |||||||
| – | – | 0,2 | 0,95 | |||||||
| – | – | 0,5 | 0,90 | |||||||
| – | 1,0 | 0,95 | ||||||||
| 0,1 | 0,90 | |||||||||
| 0,2 | 0,95 | |||||||||
| 0,5 | 0,90 | |||||||||
| – | 1,0 | 0,95 | ||||||||
| – | – | 0,1 | 0,90 | |||||||
| – | – | 0,2 | 0,95 | |||||||
| – | – | 0,5 | 0,90 | |||||||
| – | 1,0 | 0,95 | ||||||||
| 0,1 | 0,90 | |||||||||
| 0,2 | -35 | 0,95 | ||||||||
| 0,5 | 0,90 | |||||||||
| – | 1,0 | 0,95 | ||||||||
| – | – | 0,1 | 0,90 | |||||||
| – | – | 0,2 | 0,95 | |||||||
| – | – | 0,5 | 0,90 | |||||||
| – | 1,0 | 0,95 | ||||||||
| 0,1 | 0,90 | |||||||||
| -75 | -72 | -73 | -72 | -74 | 0,2 | -100 | 0,95 |
Продовження таблиці 6.5
Похибки прямих вимірювань
| Варіант |
|
|
|
|
|
|
|
|
|
|
| 0,1 | 0,90 | |||||||||
| – | 0,2 | -25 | 0,95 | |||||||
| – | – | 0,5 | -25 | 0,90 | ||||||
| 1,0 | 0,95 | |||||||||
| 0,1 | -25 | 0,90 | ||||||||
| 0,2 | 0,95 | |||||||||
| – | 0,5 | 0,90 | ||||||||
| – | – | 1,0 | 0,95 | |||||||
| – | – | 0,1 | 0,90 | |||||||
| – | – | 0,2 | 0,95 | |||||||
| – | – | 0,5 | 0,90 | |||||||
| – | – | 1,0 | 0,95 | |||||||
| – | 0,1 | 0,90 | ||||||||
| 0,2 | 0,95 | |||||||||
| 0,5 | 0,90 | |||||||||
| 1,0 | 0,95 | |||||||||
| – | 0,1 | 0,90 | ||||||||
| – | – | 0,2 | -25 | 0,95 | ||||||
| – | – | 0,5 | 0,90 | |||||||
| – | – | 1,0 | 0,95 | |||||||
| – | 0,1 | 0,90 | ||||||||
| 0,2 | 0,95 | |||||||||
| 0,5 | 0,90 | |||||||||
| 1,0 | 0,95 | |||||||||
| – | 0,1 | 0,90 | ||||||||
| – | – | 0,2 | 0,95 | |||||||
| – | – | 0,5 | 0,90 | |||||||
| -25 | 0,1 | -50 | 0,95 | |||||||
| – | 0,1 | 0,90 | ||||||||
| – | – | 0.2 | 0,95 |
Продовження таблиці 6.5
Похибки прямих вимірювань