Приклад виконання завдання А

Дані, за якими виконуються розрахунки, наведені в табл. 8.1, кінцеві результати розрахунків заносяться до табл. 8.2

 

Таблиця 8.1

Варіант
* 0,90

 

Таблиця 8.2

, %
2,122 0,082 3,9

 

Виконуємо обчислення і заносимо результати до табл. 8.3

 

Таблиця 8.3

–
–
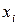
1,0 16,0 100,0 196,0 361,0 674,0
2,0 44,0 180,0 406,0 798,0 1430,0
-0,122 2,513 -3,217 -0,703 1,688 –
0,015 6,317 10,347 0,495 2,851 20,024

 

; .

З табл. 1.1 знаходимо коефіцієнт Стьюдента .

Знаходимо випадкову похибку середнього значення вимірюваної величини

.

Результат вимірювань із надійною ймовірністю подаємо у вигляді:

.

Відносна гранична похибка середнього значення вимірюваної величини

.

Відкладаємо на графіку рис. 8.1 експериментальні точки і будуємо пряму . Підставляємо в рівняння прямої . Отримуємо . Проводимо пряму через точки і .

 

Рис. 8.1. Лінійна апроксимація функцією .

Таблиця 8.4

Лінійна апроксимація.Завдання А

Варіант
0,90
0,95
0,90
0,95
0,90
0,95
0,90
0,95
0,90
0,95
0,90
0,95
0,90
0,95
0,90
0,95
0,90
0,95
0,90
0,95
0,90
0,95
0,90
0,95
0,90
0,95
0,90
0,95
0,90
0,95